Calculation of Median in Continuous Series | Formula of Median
Last Updated :
17 Aug, 2023
What is Median?
When elements in the data set are organised sequentially, that is, in either an ascending or descending order of magnitude, the median can be referred to as the middle value of the data set. Its value locates in a distribution in such a way that 50% of the items are below it and 50% are above it. It focuses on the center or middle of a distribution.
What is Continuous Series?
In continuous series (grouped frequency distribution), the value of a variable is grouped into several class intervals (such as 0-5,5-10,10-15) along with the corresponding frequencies. The method used to determine the arithmetic average in a continuous series is the same as that used in discrete series. The midpoints of several class intervals replace the class interval in a continuous series. When it is done, a continuous series and a discrete series are the same.
Example of Continuous Series
If 10 students of a class score marks between 50-60, 8 students score marks between 60-70, 12 students score marks between 70-80, and 5 students score marks between 80-90, then this information will be shown as:
Marks
| No. of Students
|
|---|
50-60
| 10
|
60-70
| 8
|
70-80
| 12
|
80-90
| 5
|
Calculation of Median in Continuous Series
The value of the median cannot be easily located for continuous series. In this situation, the median is located between the lower and upper limits of a class interval. A formula is used to interpolate (guess) the median in order to obtain the exact value. However, it should be kept in mind that when the median class of a series is first class, then the c.f. in the formula will be taken as zero. The steps required to determine median of a continuous series are as follows:
Step 1: Arrange the given data in either descending or ascending order.
Step 2: Determine the cumulative frequency; i.e., cf.
Step 3: Calculate the median item using the following formula:
![Rendered by QuickLaTeX.com Median(M)=Size~of~[\frac{N}{2}]^{th}~item](https://quicklatex.com/cache3/f9/ql_737aba75c67df1adbd3e727ab466cef9_l3.png)
Where, N = Total of Frequency
Step 4: Now inspect the cumulative frequencies and find out the cf which is either equal to or just greater than the value determined in the previous step.
Step 5: Now, find the class corresponding to the cumulative frequency equal to or just greater than the value determined in the third step. This class is known as the median class.
Step 6: Now, apply the following formula for the median:

Where,
l1 = lower limit of the median class
c.f. = cumulative frequency of the class preceding the median class
f = simple frequency of the median class
i = class size of the median group or class
Note: While calculating the median of a given distribution, we have to assume that every class of the distribution is uniformly distributed in the class interval.
Example 1:
Solution:
![Rendered by QuickLaTeX.com Median(M)=Size~of~[\frac{N}{2}]^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-eef7538dbe76795f0a1aec48857e0629_l3.png)
![Rendered by QuickLaTeX.com =Size~of~[\frac{30}{2}]^{th}~item=Siz~of~15^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5b51394eb3cee67813f9a41e8a2b885c_l3.png)
Hence, the median lies in the class 15-20.
l1 = 15, f = 8, i = 5, c.f. = 12
Now apply the following formula:
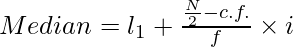
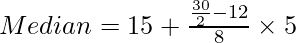
Median= 16.875
Example 2:
The distribution of income among employees has been observed in a study performed within an organisation. Determine the median wage of the organisation’s employees.
- 5 men are paid less than ₹100.
- 15 men are paid less than ₹200.
- 23 men are paid less than ₹300.
- 35 men are paid less than ₹400.
- 50 men are paid less than ₹500.
Solution:
The above frequencies are the cumulative frequencies (c.f.) of the workers. Thus to calculate the median, first, we have to convert it into simple frequency and presented the data in tabular form.
![Rendered by QuickLaTeX.com Median(M)=Size~of~[\frac{N}{2}]^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-eef7538dbe76795f0a1aec48857e0629_l3.png)
![Rendered by QuickLaTeX.com =Size~of~[\frac{50}{2}]^{th}~item=Size~of~25^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e8f0d7ef8a7ffc1d4f1f35e7147eeba2_l3.png)
Hence, the median lies in the class 300-400.
l1 = 300, f = 12, i = 100, c.f. = 23
Now apply the following formula:
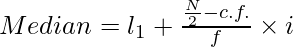
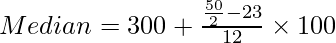
Median = 316.67
Example 3:
The weekly expenditures of 100 families are listed in the following table. Calculate the weekly expenditure’s median.
Solution:
Solution:
![Rendered by QuickLaTeX.com Median(M)=Size~of~[\frac{N}{2}]^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-eef7538dbe76795f0a1aec48857e0629_l3.png)
![Rendered by QuickLaTeX.com =Size~of~[\frac{100}{2}]^{th}~item=Size~of~50^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-61352d57c2b3c02d47df1a3412e2d1aa_l3.png)
Hence, the median lies in the class 1500-3000.
l1 = 1500, f = 25, i = 1500, c.f. = 30
Now apply the following formula:
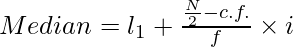
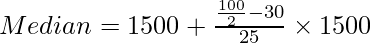
Median = 2700
Share your thoughts in the comments
Please Login to comment...