Quartile Deviation and Coefficient of Quartile Deviation: Meaning, Formula, Calculation, and Examples

Last Updated : 06 Apr, 2023

The extent to which the values of a distribution differ from the average of that distribution is known as Dispersion. The measures of dispersion can be either absolute or relative. The Measures of Absolute Dispersion consist of Range, Quartile Deviation, Mean Deviation, Standard Deviation, and Lorenz Curve.

What is Quartile Deviation?

Quartile Deviation or Semi-Interquartile Range is the half of difference between the Upper Quartile (Q₃) and the Lower Quartile (Q₁). In simple terms, QD is the half of inter-quartile range. Hence, the formula for determining Quartile Deviation is as follows:

$Quartile~Deviation=\frac{Q_3-Q_1}{2}$

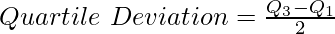
Where,

Q₃ = Upper Quartile (Size of $3[\frac{N+1}{4}]^{th}$ item)

Q₁ = Lower Quartile (Size of $[\frac{N+1}{4}]^{th}$ item)

What is Coefficient of Quartile Deviation?

As Quartile Deviation is an absolute measure of dispersion, one cannot use it for comparing the variability of two or more distributions when they are expressed in different units. Therefore, in order to compare the variability of two or more series with different units it is essential to determine the relative measure of Quartile Deviation, which is also known as the Coefficient of Quartile Deviation. It is studied to make the comparison between the degree of variation in different series. The formula for determining Coefficient of Quartile Deviation is as follows:

$Coefficient~of~Quartile~Deviation=\frac{Q_3-Q_1}{Q_3+Q_1}$

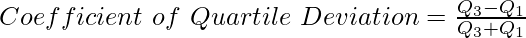
Where,

Q₃ = Upper Quartile (Size of $3[\frac{N+1}{4}]^{th}$ item)

Q₁ = Lower Quartile (Size of $[\frac{N+1}{4}]^{th}$ item)

Calculation of Quartile Deviation in Different Series

1. Individual Series:

Example:

With the help of the data given below, find the interquartile range, quartile deviation, and coefficient of quartile deviation.

Solution:

Q₁ = $Size~of~[\frac{N+1}{4}]^{th}~item=Size~of~[\frac{7+1}{4}]^{th}~item=Size~of~2^{nd}~item$

Q₁ = 140

Q₃ = $Size~of~3[\frac{N+1}{4}]^{th}~item=Size~of~3[\frac{7+1}{4}]^{th}~item=Size~of~6^{th}~item$

Q₃ = 268

Interquartile Range = Q₃ – Q₁ = 268 – 140 = 128

Quartile Deviation = $\frac{Q_3-Q_1}{2}=\frac{268-140}{2}=64$

Coefficient of Quartile Deviation = 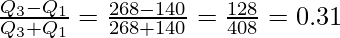$\frac{Q_3-Q_1}{Q_3+Q_1}=\frac{268-140}{268+140}=\frac{128}{408}=0.31$

Interquartile Range = 128

Quartile Deviation = 64

Coefficient of Quartile Deviation = 0.31

2. Discrete Series:

Example:

From the following table giving marks of students, calculate the interquartile range, quartile deviation, and coefficient of quartile deviation.

Solution:

Q₁ = $Size~of~[\frac{N+1}{4}]^{th}~item=Size~of~[\frac{199+1}{4}]^{th}~item=Size~of~50^{th}~item$

Q₁ = 68

Q₃ = $Size~of~3[\frac{N+1}{4}]^{th}~item=Size~of~3[\frac{199+1}{4}]^{th}~item=Size~of~150^{th}~item$

Q₃ = 88

Interquartile Range = Q₃ – Q₁ = 88 – 68 = 20

Quartile Deviation = $\frac{Q_3-Q_1}{2}=\frac{88-68}{2}=10$

Coefficient of Quartile Deviation = 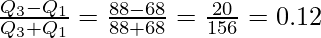$\frac{Q_3-Q_1}{Q_3+Q_1}=\frac{88-68}{88+68}=\frac{20}{156}=0.12$

Interquartile Range = 20

Quartile Deviation = 10

Coefficient of Quartile Deviation = 0.12

3. Continuous Series:

Example:

Calculate interquartile range, quartile deviation, and coefficient of quartile deviation from the following figures:

Solution:

Q₁ = $Size~of~[\frac{N}{4}]^{th}~item=Size~of~[\frac{100}{4}]^{th}~item=Size~of~25^{th}~item$

Q₁ lies in the group 20-30

l₁ = 20, c.f. = 24, f = 29, i = 10

$Q_1=l_1+\frac{\frac{N}{4}-c.f.}{f}\times{i}=20+\frac{25-24}{29}\times{10}=20+0.34$

Q₁ = 20.34

Q₃ = $Size~of~[\frac{3N}{4}]^{th}~item=Size~of~[\frac{3\times100}{4}]^{th}~item=Size~of~75^{th}~item$

Q₃ lies in the group 30-40

l₁ = 30, c.f. = 53, f = 24, i = 10

$Q_1=l_1+\frac{\frac{3N}{4}-c.f.}{f}\times{i}=30+\frac{75-53}{24}\times{10}=30+9.16$

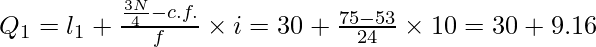
Q₃ = 39.16

Interquartile Range = Q₃ – Q₁ = 39.16 – 20.34 = 18.82

Quartile Deviation = $\frac{Q_3-Q_1}{2}=\frac{39.16-20.34}{2}=9.41$

Coefficient of Quartile Deviation = 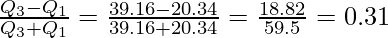$\frac{Q_3-Q_1}{Q_3+Q_1}=\frac{39.16-20.34}{39.16+20.34}=\frac{18.82}{59.5}=0.31$

Interquartile Range = 18.82

Quartile Deviation = 9.41

Coefficient of Quartile Deviation = 0.31

Suggest improvement

Partition Value | Quartiles, Deciles and Percentiles

Calculation of Mean Deviation for different types of Statistical Series

Share your thoughts in the comments

Chapter 1: Concept of Economics and Significance of Statistics in Economics

Chapter 2: Collection of Data

Chapter 3: Organisation of Data

Chapter 4: Presentation of Data: Textual and Tabular

Chapter 5: Diagrammatic Presentation of Data

Chapter 6: Measures of Central Tendency: Arithmetic Mean

Chapter 7: Measures of Central Tendency: Median and Mode

Chapter 8: Measures of Dispersion

Chapter 9: Correlation

Chapter 10: Index Number

Important Formulas in Statistics for Economics

Chapter 1: Concept of Economics and Significance of Statistics in Economics

Chapter 2: Collection of Data

Chapter 3: Organisation of Data

Chapter 4: Presentation of Data: Textual and Tabular

Chapter 5: Diagrammatic Presentation of Data

Chapter 6: Measures of Central Tendency: Arithmetic Mean

Chapter 7: Measures of Central Tendency: Median and Mode

Chapter 8: Measures of Dispersion

Chapter 9: Correlation

Chapter 10: Index Number

Important Formulas in Statistics for Economics

Quartile Deviation and Coefficient of Quartile Deviation: Meaning, Formula, Calculation, and Examples

What is Quartile Deviation?

What is Coefficient of Quartile Deviation?

Calculation of Quartile Deviation in Different Series

1. Individual Series:

Example:

Solution:

2. Discrete Series:

Example:

Solution:

3. Continuous Series:

Example:

Solution:

Please Login to comment...

Similar Reads

What kind of Experience do you want to share?