Solovay-Strassen method of Primality Test
Last Updated :
11 Jan, 2023
We have already been introduced to primality testing in the previous articles in this series.
The Solovay–Strassen primality test is a probabilistic test to determine if a number is composite or probably prime.
Before diving into the code we will need to understand some key terms and concepts to be able to code this algorithm.
Background:
Legendre Symbol: This symbol is defined as a pair of integers a and p such that p is prime. It is denoted by (a/p) and calculated as:
= 0 if a%p = 0
(a/p) = 1 if there exists an integer k such that k2 = a(mod p)
= -1 otherwise.
Euler proved that:
(a/p) = a((p-1)/2)%p Condition (i)
Jacobian Symbol: This symbol is a generalization of the Legendre Symbol, where p is replaced by n where n is
n = p1k1 * .. * pnkn
, then the Jacobian symbol is defined as:
(a/n) = ((a/p1)k1) * ((a/p2)k2) *.....* ((a/pn)kn)
If n is taken as a prime number, then the Jacobian is equal to the Legendre symbol. These symbols have certain properties –
1) (a/n) = 0 if gcd(a,n) != 1, Hence (0/n) = 0. This is because if gcd(a,n) != 1, then there must be some prime pi such that pi divides both a and n. In that case (a/pi) = 0 [by definition of the Legendre Symbol].
2) (ab/n) = (a/n) * (b/n). It can be easily derived from the fact (ab/p) = (a/p)(b/p) (here (a/p) is the Legendry Symbol).
3) If a is even, then (a/n) = (2/n)*((a/2)/n). It can be shown that:
= 1 if n = 1 ( mod 8 ) or n = 7 ( mod 8 )
(2/n) = -1 if n = 3 ( mod 8 ) or n = 5 ( mod 8 )
= 0 otherwise4) (a/n) = (n/a) * (-1)((a - 1)(n - 1) / 4) if a and n are both odd.
The Algorithm:
We select a number n to test for its primality and a random number a which lies in the range of [2, n-1] and compute its Jacobian (a/n), if n is a prime number, then the Jacobian will be equal to the Legendre and it will satisfy the condition (i) given by Euler. If it does not satisfy the given condition, then n is composite and the program will stop. Just like every other Probabilistic Primality Test, its accuracy is also directly proportional to the number of iterations. So we ran the test for several iterations to get more accurate results.
Note: We are not interested in calculating the Jacobian of even numbers as we already know that they are not prime except 2.
Pseudocode:
Algorithm for Jacobian:
Step 1 //base cases omitted
Step 2 if a>n then
Step 3 return (a mod n)/n
Step 4 else
Step 5 return (-1)((a - 1)/2)((n - 1)/2)(a/n)
Step 6 endif
Algorithm for Solovay-Strassen:
Step 1 Pick a random element a < n
Step 2 if gcd(a, n) > 1 then
Step 3 return COMPOSITE
Step 4 end if
Step 5 Compute a(n - 1)/2 using repeated squaring
and (a/n) using Jacobian algorithm.
Step 6 if (a/n) not equal to a(n - 1)/2 then
Step 7 return composite
Step 8 else
Step 9 return prime
Step 10 endif
Implementation:
C++
#include <bits/stdc++.h>
using namespace std;
long long modulo(long long base, long long exponent,
long long mod)
{
long long x = 1;
long long y = base;
while (exponent > 0)
{
if (exponent % 2 == 1)
x = (x * y) % mod;
y = (y * y) % mod;
exponent = exponent / 2;
}
return x % mod;
}
int calculateJacobian(long long a, long long n)
{
if (!a)
return 0;
int ans = 1;
if (a < 0)
{
a = -a;
if (n % 4 == 3)
ans = -ans;
}
if (a == 1)
return ans;
while (a)
{
if (a < 0)
{
a = -a;
if (n % 4 == 3)
ans = -ans;
}
while (a % 2 == 0)
{
a = a / 2;
if (n % 8 == 3 || n % 8 == 5)
ans = -ans;
}
swap(a, n);
if (a % 4 == 3 && n % 4 == 3)
ans = -ans;
a = a % n;
if (a > n / 2)
a = a - n;
}
if (n == 1)
return ans;
return 0;
}
bool solovoyStrassen(long long p, int iterations)
{
if (p < 2)
return false;
if (p != 2 && p % 2 == 0)
return false;
for (int i = 0; i < iterations; i++)
{
long long a = rand() % (p - 1) + 1;
long long jacobian = (p + calculateJacobian(a, p)) % p;
long long mod = modulo(a, (p - 1) / 2, p);
if (!jacobian || mod != jacobian)
return false;
}
return true;
}
int main()
{
int iterations = 50;
long long num1 = 15;
long long num2 = 13;
if (solovoyStrassen(num1, iterations))
printf("%d is prime\n",num1);
else
printf("%d is composite\n",num1);
if (solovoyStrassen(num2, iterations))
printf("%d is prime\n",num2);
else
printf("%d is composite\n",num2);
return 0;
}
|
Java
import java.util.Scanner;
import java.util.Random;
class GFG{
static long modulo(long base,
long exponent,
long mod)
{
long x = 1;
long y = base;
while (exponent > 0)
{
if (exponent % 2 == 1)
x = (x * y) % mod;
y = (y * y) % mod;
exponent = exponent / 2;
}
return x % mod;
}
static long calculateJacobian(long a, long n)
{
if (n <= 0 || n % 2 == 0)
return 0;
long ans = 1L;
if (a < 0)
{
a = -a;
if (n % 4 == 3)
ans = -ans;
}
if (a == 1)
return ans;
while (a != 0)
{
if (a < 0)
{
a = -a;
if (n % 4 == 3)
ans = -ans;
}
while (a % 2 == 0)
{
a /= 2;
if (n % 8 == 3 || n % 8 == 5)
ans = -ans;
}
long temp = a;
a = n;
n = temp;
if (a % 4 == 3 && n % 4 == 3)
ans = -ans;
a %= n;
if (a > n / 2)
a = a - n;
}
if (n == 1)
return ans;
return 0;
}
static boolean solovoyStrassen(long p,
int iteration)
{
if (p < 2)
return false;
if (p != 2 && p % 2 == 0)
return false;
Random rand = new Random();
for(int i = 0; i < iteration; i++)
{
long r = Math.abs(rand.nextLong());
long a = r % (p - 1) + 1;
long jacobian = (p + calculateJacobian(a, p)) % p;
long mod = modulo(a, (p - 1) / 2, p);
if (jacobian == 0 || mod != jacobian)
return false;
}
return true;
}
public static void main (String[] args)
{
int iter = 50;
long num1 = 15;
long num2 = 13;
if (solovoyStrassen(num1, iter))
System.out.println(num1 + " is prime");
else
System.out.println(num1 + " is composite");
if (solovoyStrassen(num2,iter))
System.out.println(num2 + " is prime");
else
System.out.println(num2 + " is composite");
}
}
|
Python3
import random
def modulo(base, exponent, mod):
x = 1;
y = base;
while (exponent > 0):
if (exponent % 2 == 1):
x = (x * y) % mod;
y = (y * y) % mod;
exponent = exponent // 2;
return x % mod;
def calculateJacobian(a, n):
if (a == 0):
return 0;
ans = 1;
if (a < 0):
a = -a;
if (n % 4 == 3):
ans = -ans;
if (a == 1):
return ans;
while (a):
if (a < 0):
a = -a;
if (n % 4 == 3):
ans = -ans;
while (a % 2 == 0):
a = a // 2;
if (n % 8 == 3 or n % 8 == 5):
ans = -ans;
a, n = n, a;
if (a % 4 == 3 and n % 4 == 3):
ans = -ans;
a = a % n;
if (a > n // 2):
a = a - n;
if (n == 1):
return ans;
return 0;
def solovoyStrassen(p, iterations):
if (p < 2):
return False;
if (p != 2 and p % 2 == 0):
return False;
for i in range(iterations):
a = random.randrange(p - 1) + 1;
jacobian = (p + calculateJacobian(a, p)) % p;
mod = modulo(a, (p - 1) / 2, p);
if (jacobian == 0 or mod != jacobian):
return False;
return True;
iterations = 50;
num1 = 15;
num2 = 13;
if (solovoyStrassen(num1, iterations)):
print(num1, "is prime ");
else:
print(num1, "is composite");
if (solovoyStrassen(num2, iterations)):
print(num2, "is prime");
else:
print(num2, "is composite");
|
C#
/// C# program to implement Solovay-Strassen
using System;
using System.Collections.Generic;
class GFG {
static long modulo(long Base, long exponent, long mod)
{
long x = 1;
long y = Base;
while (exponent > 0)
{
if (exponent % 2 == 1)
x = (x * y) % mod;
y = (y * y) % mod;
exponent = exponent / 2;
}
return x % mod;
}
static long calculateJacobian(long a, long n)
{
if (n <= 0 || n % 2 == 0)
return 0;
long ans = 1L;
if (a < 0)
{
a = -a;
if (n % 4 == 3)
ans = -ans;
}
if (a == 1)
return ans;
while (a != 0)
{
if (a < 0)
{
a = -a;
if (n % 4 == 3)
ans = -ans;
}
while (a % 2 == 0)
{
a /= 2;
if (n % 8 == 3 || n % 8 == 5)
ans = -ans;
}
long temp = a;
a = n;
n = temp;
if (a % 4 == 3 && n % 4 == 3)
ans = -ans;
a %= n;
if (a > n / 2)
a = a - n;
}
if (n == 1)
return ans;
return 0;
}
static bool solovoyStrassen(long p, int iteration)
{
if (p < 2)
return false;
if (p != 2 && p % 2 == 0)
return false;
Random rand = new Random();
for(int i = 0; i < iteration; i++)
{
long r = Math.Abs(rand.Next());
long a = r % (p - 1) + 1;
long jacobian = (p + calculateJacobian(a, p)) % p;
long mod = modulo(a, (p - 1) / 2, p);
if (jacobian == 0 || mod != jacobian)
return false;
}
return true;
}
static void Main()
{
int iter = 50;
long num1 = 15;
long num2 = 13;
if (solovoyStrassen(num1, iter))
Console.WriteLine(num1 + " is prime");
else
Console.WriteLine(num1 + " is composite");
if (solovoyStrassen(num2,iter))
Console.WriteLine(num2 + " is prime");
else
Console.WriteLine(num2 + " is composite");
}
}
|
PHP
<?php
function modulo($base, $exponent, $mod)
{
$x = 1;
$y = $base;
while ($exponent > 0)
{
if ($exponent % 2 == 1)
$x = ($x * $y) % $mod;
$y = ($y * $y) % $mod;
$exponent = $exponent / 2;
}
return $x % $mod;
}
function calculateJacobian($a, $n)
{
if (!$a)
return 0;
$ans = 1;
if ($a < 0)
{
$a = -$a;
if ($n % 4 == 3)
$ans = -$ans;
}
if ($a == 1)
return $ans;
while ($a)
{
if ($a < 0)
{
$a = -$a;
if ($n % 4 == 3)
$ans = -$ans;
}
while ($a % 2 == 0)
{
$a = $a / 2;
if ($n % 8 == 3 || $n % 8 == 5)
$ans = -$ans;
}
list($a, $n) = array($n, $a);
if ($a % 4 == 3 && $n % 4 == 3)
$ans = -$ans;
$a = $a % $n;
if ($a > $n / 2)
$a = $a - $n;
}
if ($n == 1)
return $ans;
return 0;
}
function solovoyStrassen($p, $iterations)
{
if ($p < 2)
return false;
if ($p != 2 && $p % 2 == 0)
return false;
for ($i = 0; $i < $iterations; $i++)
{
$a = rand() % ($p - 1) + 1;
$jacobian = ($p +
calculateJacobian($a,
$p)) % $p;
$mod = modulo($a, ($p - 1) / 2, $p);
if (!$jacobian || $mod != $jacobian)
return false;
}
return true;
}
$iterations = 50;
$num1 = 15;
$num2 = 13;
if (solovoyStrassen($num1, $iterations))
echo $num1," is prime ","\n";
else
echo $num1," is composite\n";
if (solovoyStrassen($num2, $iterations))
echo $num2," is prime\n";
else
echo $num2," is composite\n";
?>
|
Javascript
<script>
function modulo( base, exponent,mod)
{
let x = 1;
let y = base;
while (exponent > 0)
{
if (exponent % 2 == 1)
x = (x * y) % mod;
y = (y * y) % mod;
exponent = Math.floor(exponent / 2);
}
return x % mod;
}
function calculateJacobian( a, n)
{
if (n <= 0 || n % 2 == 0)
return 0;
let ans = 1;
if (a < 0)
{
a = -a;
if (n % 4 == 3)
ans = -ans;
}
if (a == 1)
return ans;
while (a != 0)
{
if (a < 0)
{
a = -a;
if (n % 4 == 3)
ans = -ans;
}
while (a % 2 == 0)
{
a = Math.floor(a/2);
if (n % 8 == 3 || n % 8 == 5)
ans = -ans;
}
let temp= a;
a = n;
n = temp;
if (a % 4 == 3 && n % 4 == 3)
ans = -ans;
a %= n;
if (a > Math.floor(n / 2))
a = a - n;
}
if (n == 1)
return ans;
return 0;
}
function solovoyStrassen( p, iteration)
{
if (p < 2)
return false;
if (p != 2 && p % 2 == 0)
return false;
for(let i = 0; i < iteration; i++)
{
let r = Math.floor(Math.random()* (Number.MAX_VALUE, 2) );
let a = r % (p - 1) + 1;
let jacobian = (p + calculateJacobian(a, p)) % p;
let mod = modulo(a, Math.floor((p - 1) / 2), p);
if (jacobian == 0 || mod != jacobian)
return false;
}
return true;
}
let iter = 50;
let num1 = 15;
let num2 = 13;
if (solovoyStrassen(num1, iter))
document.write(num1 + " is prime"+ "</br>");
else
document.write(num1 + " is composite" + "</br>");
if (solovoyStrassen(num2,iter))
document.write(num2 + " is prime"+ "</br>");
else
document.write(num2 + " is composite"+ "</br>");
</script>
|
Output :
15 is composite
13 is prime
Running Time: Using fast algorithms for modular exponentiation, the running time of this algorithm is O(k·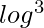 n), where k is the number of different values we test.
n), where k is the number of different values we test.
Auxiliary Space: O(1) as it is using constant space for variables
Accuracy: It is possible for the algorithm to return an incorrect answer. If the input n is indeed prime, then the output will always probably be correctly prime. However, if the input n is composite, then it is possible for the output to probably be incorrect prime. The number n is then called an Euler-Jacobi pseudoprime.
Share your thoughts in the comments
Please Login to comment...