Nonhomogeneous Poisson Processes
Last Updated :
21 Sep, 2018
Non-homogeneous Poisson process model (
NHPP) represents the number of failures experienced up to time
t is a non-homogeneous Poisson process {N(t), t ≥ 0}.
The main issue in the NHPP model is to determine an appropriate mean value function to denote the expected number of failures experienced up to a certain time.
With different assumptions, the model will end up with different functional forms of the mean value function. Note that in a renewal process, the exponential assumption for the inter-arrival time between failures is relaxed, and in the NHPP, the stationary assumption is relaxed.
Non-homogeneous Poisson process model is based on the following assumptions:
–>The failure process has an independent increment, i.e. the number of failures during the time interval (t, t + s) depends on the current time t and the length of time interval s, and does not depend on the past history of the process.
–> The failure rate of the process is given by P{exactly one failure in (t, t + ∆t)} = P{N(t, t + ∆t) – N(t)=1} = 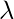 (t)∆t + o(∆t) where
(t)∆t + o(∆t) where 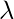 (t) is the intensity function.
–> During a small interval ∆t, the probability of more than one failure is negligible, that is, P{two or more failure in (t, t+∆t)} = o(∆t)
–> The initial condition is N(0) = 0.
(t) is the intensity function.
–> During a small interval ∆t, the probability of more than one failure is negligible, that is, P{two or more failure in (t, t+∆t)} = o(∆t)
–> The initial condition is N(0) = 0.
On the basis of these assumptions, the probability of exactly n failures occurring during the time interval (0, t) for the NHPP is given by
![Rendered by QuickLaTeX.com Pr\begin{Bmatrix}N(t)=n\end{Bmatrix} = \frac{[m(t)]^{n}}{n!}e^{-m(t)}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fea9cbd2fbfcc086481ffe0d1f9d7a09_l3.png)
where
![Rendered by QuickLaTeX.com m(t)=E[N(t)]=\int_{0}^{t}\lambda \left ( s\right )ds](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-33f9beb2526d947514450cb3cc0749b5_l3.png)
and
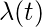
is the intensity function. It can be easily shown that the mean value function m(t) is non-decreasing.
Reliability Function:
The reliability R(t), defined as the probability that there are no failures in the time interval (0, t), is given by
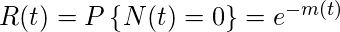
In general, the reliability R(x|t), the probability that there are no failures in the interval (t, t + x), is given by
![Rendered by QuickLaTeX.com R(x|t)=P\left \{ N(t+x)-N(t)=0 \right \} = e^{-[m(t+x)-m(t)]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-58de9c70887f8bf50422470563c268d9_l3.png)
and its density is given by
![Rendered by QuickLaTeX.com f(x)=\lambda (t+x)e^{-[m(t+x)-m(t)]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-88d0c0f2b38b7eb6bffbaf3194678e6c_l3.png)
where
![Rendered by QuickLaTeX.com \lambda (x)=\frac{\partial [m(x)]}{\partial x}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-75a4a3b2e29ceb47206d574d0ca70c3a_l3.png)
The variance of the NHPP can be obtained as follows:
![Rendered by QuickLaTeX.com Var[N(t)]=\int_{0}^{t}\lambda (s)ds](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-35b8d528a7f4df43f9c07f8e42944b1a_l3.png)
Share your thoughts in the comments
Please Login to comment...