Mensuration is the branch of geometry that deals with the measurement of area, length, or volume in 2D and 3D shapes. The 2D and 3D shapes are often called geometric shapes. In this article, we have curated all the mensuration formulas for various 2-D and 3-D shapes in detail.
Mensuration Definition
Mensuration is measuring various parameters of 2-D and 3-D shapes. We see various 3-D shapes in our daily lives whose parameters we have to find. So, mensuration formulas are deduced to solve our problems. With the help of mensuration formulas, we can find the area, perimeter, and volume of various objects.
Types of Geometrical Shapes
Geometrical shapes of various types are broadly categorized into two different categories.
- 2-Dimensional Shapes
- 3-Dimensional Shapes
Two Dimensional Shapes
2D objects have only two dimensions, width and length, but no thickness. Like a square, rectangle, triangle, or circle. In mathematical representation, it has Two-axis (X and Y). Having only two-axis and no thickness, these 2D objects do not exist in the real world and can be represented only by using plain surfaces.
Examples of various 2-D shapes are Circle, Triangle, Rectangle, Square, etc.

Learn More :
Three Dimensional Shapes
In 3D objects have three dimensions (such as height, width, and depth), like any object in the real world. The 3D shapes are called solid shapes. In mathematical representation, it has three-axis (X, Y, and Z). Unlike 2D shapes, 3D shapes have more parameters to cover. 3D objects have some volume and Total Surface area that uses all three dimensions i.e. length, width, and depth of the object.
Examples of various 3-D shapes are Pyramid, Prism, Cube, Cuboid, etc.

Learn More :
Mensuration Formulas
Mensuration formulas involve all mensuration formulas for both 3D and 2D shapes. The most commonly used formula is the surface area and volume of these shapes. However, let us learn all the formulas for these shapes.
Mensuration Formulas for 2D shapes
Formulas for the surface area and perimeter of 2D Shapes are discussed below in this article:
Rectangle
A rectangle is a 2D shape, having 4 sides and 4 corners. The rectangle is a quadrilateral with four right angles, so, each angle is 90°. The sum of all the interior angles is equal to 360 degrees. The opposite sides are parallel and equal to each other. Diagonals of a rectangle have the same length.

Various formulas of the rectangle are,
- Perimeter of a Rectangle = 2 (Length + Breadth)
- Area of a Rectangle = Length × Breadth
Learn More :
Square
A square is a 2D shape plane figure with four equal sides and all four angles are equal to 90 degrees. Diagonals of a square are of equal length.

Various formulas of the square are,
- Area of a Square = (Side)2
- Perimeter of a Square = 4(Side)
Learn More :
Circle
A circle is a basic 2D shape, and it is a set of points in a plane that are equidistant from the centre. The distance between the centre and any point on the circumference is called the radius.

Various formulas of the circle are,
- Diameter of a Circle = 2 × Radius
- Circumference of a Circle = π × Diameter or 2 × π × Radius
- Area of a Circle = π × Radius2
Learn More :
Triangle
A triangle has three sides and three inclusive angles. All three angles of a triangle always add up to 180°.

Various formulas of the triangle are,
- Area of a Triangle = ½ × b × h
- Perimeter of Triangle = Sum of All Sides
Learn More :
Parallelogram
A parallelogram is a 2D shape whose opposite sides are parallel to each other, It has four sides, where the pair of parallel sides are equal in length.

Various formulas of the parallelogram are,
- Perimeter of a Parallelogram = 2 (a+b)
- Area of a Parallelogram = b × h
Trapezium
Trapezium is a quadrilateral with exactly one pair of parallel sides. This means that two opposite sides are parallel while the other two sides are not.

Various formulas of the Trapezium are,
- Perimeter of Trapezium = a + b + c + d[Where a & b are parallel sides and c & d are non-parallel sides.]
- Area of Trapezium =1/2 (a+b) × h
Note: Trapezium is also called Trapezoid.
Learn More:
Rhombus
A rhombus is a type of quadrilateral, which is a polygon with four sides. Specifically, a rhombus is a quadrilateral with all four sides of equal length. It is often referred to as a diamond or a rhomb.

Various formulas of the rhombus are,
- Perimeter of Rhombus = 4s
- Area of Rhombus = 1/2 × d1 × d2
Learn More
Summary for 2D Shapes
Summary of formulas for 2D shapes are:
| Shape |
Formula |
|
Triangle
|
Perimeter = a + b + c |
| Area = 1/2 × base × height |
| Square |
Perimeter = 4s |
| Area = s2 |
| Rectangle |
Perimeter = 2(l + w) |
| Area = lw |
| Parallelogram |
Perimeter = 2(a + b) |
| Area = bh |
| Circle |
Circumference = 2πr |
| Area = πr² |
| Trapezium |
Perimeter = a + b + c + d |
| Area = 1/2 × (a + b) × h |
| Rhombus |
Perimeter = 4s |
| Area = 1/2 × d1 × d2 |
Where,
- s is the length of a side.
- l is the length of the rectangle.
- w is the width of the rectangle.
- a, b, c, are d are the lengths of the sides of the trapezoid.
- h is the height of the shape.
- r is the radius of the circle.
- d1 and d2 are the diagonals of the rhombus.
Learn More :
Mensuration Formulas for 3D Shapes
Mensuration Formula of 3D Shapes are discussed below in this article.
Cube
Cube is a solid 3D figure, which has 6 square faces, 8 vertices, and 12 edges, such that 3 edges meet at one vertex point. An example of a cube is a piece of Sugar or ice with six square sides.

Various formulas of the Cube are,
- Volume of a Cube = side3 cubic units
- Lateral Surface Area of a Cube= 4 × side2 sq. units
- Total Surface Area of a Cube= 6 × side2 sq. units
- Diagonal of Cube = √3.(side)
Learn More :
Cuboid
A cuboid is a 3D figure with three sides where all the sides are not equal. All of its faces are rectangles having a total of 6 faces, 8 vertices, and 12 edges.

Various cuboid formulas are,
- Volume of a Cuboid = (length × width × height) cubic units
- Lateral Surface Area of a Cuboid = 2 × height (length + width) sq. units
- Total Surface Area of a Cuboid = 2(length × width + length × height + height × width) sq. units
- Diagonal length of a Cuboid = √(length2 + breadth2 + height2) units
Learn More :
Sphere
A sphere is an object that is an absolutely round geometrical shape in 3D space. It is the set of all points in a space equidistant from a given point called the centre of the sphere. The distance between any point of the sphere and its centre is called the radius(R).

Various sphere formulas are,
- Volume of a Sphere = 4/3 × π × (radius)³ cubic units
- Surface Area of a Sphere = 4 × π × (radius)² sq. units
Learn More :
Hemisphere
A Hemisphere is a 3-D figure. That is formed by taking half of the sphere and hence is called the Hemisphere. A hemisphere has two surface.

Various Hemisphere formulas are,
- Volume of Hemisphere = 2/3 × π × (radius)² × (height) cubic units
- Curved Surface Area of Hemisphere = 2π × (radius)²
- Total Surface Area of Hemisphere = 3π × (radius)²
Learn More :
Cone
A cone is a three-dimensional geometric shape. It is formed by using a set of line segments or the lines which connect a common point, called the apex or vertex. The base of a cone it has circular, so we can compute the value of the radius. And the length of the cone from the apex to any point on the circumference of the base is the slant height.

Various cone formulas are,
- Volume of Cone = 1/3 × π × (radius)² × (height) cubic units
- Curved Surface Area of Cone = π × radius × slant height square units
- Total Surface Area of Cone = π × radius × (slant height + radius) square units
Learn More:
Cylinder
Cylinder is a 3-D figure formed by three surface, one rectange surface and two circular faces. In cylinder the rectangular surface is curved to form a curved surface and the circular surface forms the base and top of the cylinder.

Various cylinder formulas are,
- Volume of Cylinder = π × (radius)² × (height) cubic units
- Curved Surface Area of Cykinder = 2π × (radius) × (height) square units
- Total Surface Area of Cylinder = 2π × (radius) × (height + radius) square units
Pyramid
A pyramid is a three-dimensional geometric shape that consists of a polygonal base and triangular faces that meet at a single point called the apex or vertex.
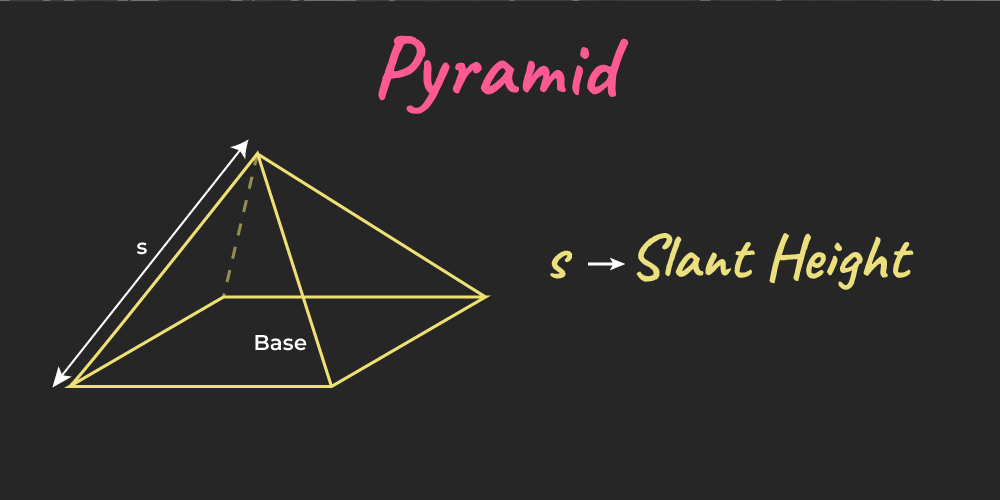
Different formulas for pyramid are:
- Lateral Surface Area = 1/2 × Perimeter of base × slant height
- Total Surface Area = (1/2 × Perimeter of base × slant height) + Base Area
- Volume = 1/3 × Base Area × Height
Learn More:
Summary for 3D Shapes
Summary of formulas for 3D shapes are:
| Shape |
Formula |
| Cube |
Lateral Surface Area = 4s2
|
| Total Surface Area = 6s2 |
| Volume = s3 |
| Cuboid |
Lateral Surface Area = 2 × h (l + w)
|
| Surface Area = 2lw + 2lh + 2wh |
| Volume = l × w × h |
| Sphere |
Surface Area = 4πr2 |
| Volume = 4/3 πr³ |
| Hemisphere |
Curved Surface Area = 2πr2
|
| Total Surface Area = 2πr2 + πr2 |
| Volume = 2/3 πr3 |
| Cylinder |
Curved Surface Area = 2πrh |
| Total Surface Area = 2πr2 + 2πrh |
| Volume = πr2h |
| Cone |
Curved Surface Area = πrl |
| Total Surface Area = πr2 + πrl |
| Volume = 1/3 πr2h |
| Pyramid |
Surface Area = (1/2 × Perimeter of base × slant height) + Base Area |
| Volume = 1/3 × Base Area × Height |
Where,
- s is the length of a side (for cube).
- l is the length, w is the width, and h is the height (for cuboid).
- r is the radius of the sphere, hemisphere, cylinder, or cone.
- h is the height of the cylinder or cone.
- l is the slant height of the cone
Learn More
Solved Examples on Mensuration
Example 1: Find the area of a square with a side of 15 cm.
Solution:
Area of a square = side × side
Here, side = 15 cm
Area = 15 × 15= 225
Therefore, the area of the square = 225 cm2
Example 2: Find the area and perimeter of a square whose side is 25 cm.
Solution:
Side = a = 25 cm
Area of a square = a2 square units
⇒ Area of a square = 252
⇒ Area of square = 25 × 25
⇒ Area of square = 625
Therefore, area of a square = 625 cm2
Perimeter of a Square = 4a units
⇒ P = 4 × 25 =100
Therefore, perimeter of a square is 100 cm
Example 3: Find the surface area of a cuboid with a length of 3 units, a width of 4 units, and a height of 5 units.
Solution:
Given,
Length of the cuboid = 3 units
Breadth of the cuboid = 4 units
Height of the cuboid = 5 units
Surface Area of cuboid = 2 × (lb + bh + lh) square units
⇒ Surface Area of cuboid = 2[(3 × 4) + (4 × 5) + (3 × 5)]
⇒ Surface Area of cuboid = 2(12 + 20 + 15)
⇒ Surface Area of cuboid = 2(47)
⇒ Surface Area of cuboid = 94 square units
Therefore, surface area of the cuboid is 94 square units.
Example 4: Find the area and circumference of a circle whose radius is 7 cm.
Solution:
Radius of circle = 7 cm
Area of a circle = π × r2 (π = 22/7)
⇒ Area of a circle = 22/7 × 7 × 7
⇒ Area of a circle = 154 cm2
Therefore, Area of the circle = 154 square cm
⇒ Circumference of a circle = 2πr
⇒ Circumference of a circle = 2 × (22/7) × 7
⇒ Circumference of a circle = 44 cm
Therefore, circumference of the circle is 44 cm
Mensuration Practice Questions
Q1: Find the area of an equilateral triangle of side 24cm.
Q2: Find the volume, lateral surface area, total surface area and diagonal of a cuboid whose length, breadth and height are 10 cm, 15 cm and 20 cm respectively.
Q3: Find the volume, lateral surface area, total surface area and diagonal of a cube whose each side measures 15 cm.
Q4: Find the volume, curved surface area, total surface area of a cylinder whose radius is 21 cm and height is 14 cm.
Q5: Find the volume, curved surface area, total surface area of a cone whose radius is 7 cm and height is 14 cm.
Q6: Find the volume and surface area of a sphere of radius 28 cm.
Q7: Find the volume, curved surface area, total surface area of a hemisphere whose radius is 18 cm.
Mensuration Formulas – FAQs
Who Introduced Mensuration?
Archimedes was credited for the introduction of mensuration. He is one of the greatest mathematicians of the ancient era. He was the first to formulate the perimeter and the area of various 2-D shapes.
What is Mensuration in Maths?
Mensuration in mathematics is defined as the study of the measurement such as the area and perimeter of various 2D and 3D geometric shapes.
What is Difference Between Mensuration and Geometry?
Mensuration is the study of the calculation of various parameters of 2-D and 3-D shapes such as the perimeter, area, volume, etc. while in geometry we deal with the study of properties and relations of points and lines of various shapes.
What is Volume of Sphere?
Volume of sphere is defined as the total capacity of material a sphere can hold. For a sphere of radius “r” the voume is calculated using the formula,
Volume of Sphere = 4/3π(r3)
It is measured in cubic units.
What is Surface Area of Cone?
Surface Area of Cone is defined as the total space occupied by the Cone. It is also called the total surface area (TSA) of cone. For a cone of radius “r” and slant height “l” the surface area is calculated using the formula,
TSA of Cone = πr(l + r)
It is measured in square units.
Share your thoughts in the comments
Please Login to comment...