Volume of Cylinder refers to the amount of space contained within its three-dimensional boundaries. Imagine a soda can or a piece of pipe – these objects resemble cylinders and have a certain amount of internal space. To quantify this space, we use the concept of volume.
A cylinder is a -dimensional solid figure with two identical bases connected by a curving surface. It can be visualized as a stack of circular discs which are placed on top of each other. For any cylinder, the perpendicular distance between the bases(both bottom and top) is called the height of a cylinder, and the radius of any of its bases is the radius of the cylinder. A cylinder has two circular bases and a curved lateral surface connecting the bases. Surface area of a cylinder is the total area of all its curved and flat surfaces.
In this article, we will study everything about what is the volume of cylinder, volume of cylinder formula, and how to calculate the volume of a cylinder.
What is the Volume of Cylinder?
Volume of the cylinder is the total capacity of any cylinder, i.e. the total amount of liquid any cylinder can hold. It is generally measured in litres but as litres and cubic units are two units that can be converted into each other, the volume can also be measured in m3, cm3, etc, or converted in m3 from litres and vice versa. It is calculated by multiplying the area of the base of the cylinder by its height.
While a cylinder and a prism have similarities, it’s important to note that a cylinder isn’t exactly the same as a prism because a cylinder has a curved side surface. But, we can still use the same formula to calculate the volume of both a cylinder and a prism.
Volume of Cylinder Definition:
Volume of cylinder is a measure of the space enclosed by its three-dimensional shape.
The volume of a cylinder is also equal to the amount of space taken by it in a three-dimensional space. In other words, it determines the space or region enclosed by the cylinder is its volume, and the unit of volume is cubic unit i.e., the number of unit cubes (cubes of unit length) that may fit into an object.
Volume of Cylinder
Volume of Right Circular Cylinder
In the Right Circular Cylinder angle between the plane of the base or top and the curved surface is a right angle. For a right circular cylinder, the base is a circle with radius r, thus its area is πr2, and the height of the cylinder is h then the volume of the cylinder is:
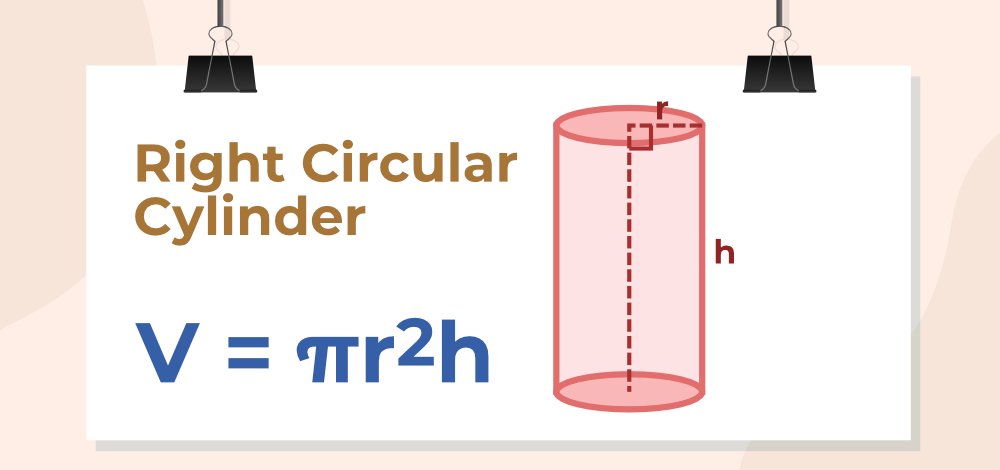
Volume of Right Circular Cylinder
Volume of Hollow Cylinder
A hollow cylinder is a cylinder that is hollow from the inside thus, its bases form a ring with two radii inner radius and an outer radius. Suppose a hollow cylinder is taken with its inner radius as r and outer radius as R and the height of the cylinder is h then,
Volume of a Hollow Cylinder
Volume of Oblique Cylinder
In an Oblique Cylinder angle between the plane of the base or top and the curved surface is not a right angle, but volume is given by the same formula as a product of the area of the base and the height of the cylinder.
Volume of Oblique Cyllinder
Volume of Elliptic Cylinder
A cylinder; with an ellipse as its base instead of a circle, is known as Elliptic Cylinder. Let both radii of the base which is an ellipse be a and b and the height of the cylinder be h, then
Volume of Elliptic Cylinder
How To Find the Volume of Cylinder?
Let’s take an example to understand how we can calculate the volume of a cylinder.
Example: Calculate the volume of a cylinder of radius 4 m and height 5 m.
Step 1: Note the radius and height of cylinder. In this example, the radius of the cylinder is 4 m and height is 5 m.
Step 2: We know that the volume of a cylinder is equal to πr2h. Substitute the given value of radius and height in the formula.
Step 3: So, the volume of cylinder is calculated as, 3.14 × (4)2 × 5 = 251.20 cu. m.
Volume of Cylinder in Liters
Generally, the volume of a cylinder is calculated in cubic meters or cubic centimetres but we can change them in litres by using the conversion discussed below i.e.,
1 cm3 = 1 ml,
1000 cm3 = 1 litre,
1 m3 = 1000000 cm3 = 1000 litres
Example: If a cylinder has a volume of 32 m3 it can be written as 32×1000 litres = 32000 litres
Surface Area of Cylinder
Surface Area of any figure is defined as the area required to totally cover the surface of any object. So, the surface area of a cylinder can be defined as the area required to cover the surface of the cylinder.
CSA of Cylinder
Curved Surface Area or CSA is the area of the surface that is not flat but rounded. So, the CSA of the cylinder is all the surface except the base and top. If r is the radius of the base and h is the height of the cylinder, then CSA is given as follows:
CSA of Cylinder = 2πrh
TSA of Cylinder
Total Surface Area or TSA is the area of the completer surface of the cylinder. So, TSA is the sum of the CSA and the area of the top as well as the base of the cylinder. So, if the base radius of the cylinder is r and the height of the cylinder is h then TSA is given by,
TSA of cylinder = 2πr(r+h)
Related Resources,
Solved Examples on the Volume of Cylinder
Problem 1: Calculate the volume of a cylinder of radius 3 m and a height of 4 m. (take π = 3.14)
Solution:
We have, r = 3 and h = 4
Using the formula we have,
V = πr2h
⇒ V = 3.14 × (3)2 × 4
⇒ V = 113.04 m3
Problem 2: Calculate the volume of a cylinder of radius 4 m and a height of 7 m.
Solution:
We have, r = 4 and h = 7
Using the formula we have,
V = πr2h
⇒ V = 3.14 × (4)2 × 7
⇒ V = 351.68 m3
Problem 3: Calculate the radius of a cylinder if its volume is 300 m3 and height is 7 m.
Solution:
We have, V = 300 and h = 7
Using the formula we have,
V = πr2h
⇒ r2 = V/πh
⇒ r2 = 300/(3.14 × 7)
⇒ r = 3.68 m
Problem 4: Calculate the radius of a cylinder if its volume is 450 m3 and its height is 9 m.
Solution:
We have, V = 450 and h = 9
Using the formula we have,
V = πr2h
⇒ r2 = V/πh
⇒ r2 = 450/(3.14 × 9)
⇒ r = 12.52 m
Problem 5: Calculate the height of a cylinder if its volume is 570 m3 and its radius is 4 m.
Solution:
We have, V = 570 and r = 4
Using the formula we have,
V = πr2h
⇒ h = V/πr2
⇒ h = 570/(3.14 × 4 × 4)
⇒ h = 11.34 m
Problem 6: Calculate the height of a cylinder if its volume is 341 m3 and its radius is 6 m.
Solution:
We have,
V = 341 m3
r = 6 m
Using the formula we have,
V = πr2h
⇒ h = V/πr2
⇒ h = 341/(3.14 × 6 × 6)
⇒ h = 3.01 m
Practice Questions on Volume of Cylinder
Q1: Find the Volume of Cylinder whose diameter is 14 cm and height is 12 cm.
Q2: Find the Volume of Cylinder whose surface area of base is 84 cm2 and height is 11 cm.
Q3: Find the height of cylinder whose radius is 7 cm and volume is 770 cm3
Q4: Find the volume of a hollow cylinder of height 13 cm whose inner radius is 6 cm and outer radius is 1 cm.
FAQs on Volume of Cylinder
1. What is meant by the Volume of Cylinder?
The volume of a cylinder is defined as the capacity of the cylinder, i.e, the amount of substance a cylinder can hold. It can also be defined as the total material required for making a cylinder.
Volume of the cylinder (V) is given by,
V = (Area of circular base) × (Height)
V = πr2h
where,
r is radius of base
h is height of cylinder
2. By what factor is the Volume of the Cylinder changed if its radius is doubled?
We already know that volume of cylinder is directly proportional to the square of its radius.(volume of cylinder ∝ Radius2)
So if the radius is doubled, (i.e., r = 2r), we get
V = πr2h
⇒ V = π(2r)2h
⇒ V = 4πr2h.
Hence, the volume of cylinder becomes four times its initial value, when its radius is doubled.
3. By what factor is the Volume of the Cylinder changed if its Radius is halved?
We already know that volume of cylinder is directly proportional to the square of its radius.(volume of cylinder ∝ Radius2)
So if the radius is halved, (i.e., r = r/2), we get
V = π(r/2)2h
⇒ V = (πr2h)/4
Thus, the volume of cylinder becomes one-fourth its initial value, when its radius is halved.
4. What is the Unit for the Volume of a Cylinder?
Volume of a cylinder is normally measured in cubic units, i.e. cubic centimeters (cm3), cubic meters (m3), cubic feet (ft3) and so on for mathematical purposes. In general usage, it is measured in Liters(l), milliliters(ml), etc.
5. Find the Volume of Cylinder with Diameter ‘d’ units and Height ‘h’ units.
If the diameter of a cylinder is d then its radius is given by radius = (diameter)/2 so r = d/2
V = πr2h
⇒ V= π(d/2)2h
⇒ V = πdh / 4 unit 3
6. How to calculate the Volume of a Hollow Cylinder?
If R is the external radius and r is the internal radius, then the formula for calculating the cylinder’s volume is given by:
V = π (R2 – r2) h cubic units.
7. What is the volume of cylinder calculator?
Volume of cylinder calculator is a tool which is used to find volume of the cylinder by inputting the value of radius and height of the cylinder.