Standard Deviation: Meaning, Coefficient of Standard Deviation, Merits, and Demerits
Last Updated :
06 Apr, 2023
The methods of measuring dispersion such as quartile deviation, range, mean deviation, etc., are not universally adopted as they do not provide much accuracy. Range does not provide required satisfaction as in the entire group, range’s magnitude is determined by most extreme cases. Quartile Deviation does not have algebraic properties and it is also difficult to interpret it. However, Mean Deviation ignores the deviation’s algebraic signs making it unsatisfactory. All these issues increased the need for a measure of dispersion which is free from these shortcomings, which was to some extent is solved by Standard Deviation.
What is Standard Deviation?
A scientific measure of dispersion that is widely used in statistical analysis of a given set of data is known as Standard Deviation. Another name for standard deviation is Root Mean Square Deviation (as it is the square root of the means of squared deviations from the arithmetic mean). Standard Deviation is denoted by the Greek Symbol σ (sigma) and was first used in 1893 by Karl Pearson. Under this method, the square root of the arithmetic average of the squares of the deviations is determined. The deviation of values is taken from the arithmetic mean of the given set of data.
According to Spiegel, “The Standard Deviation is the square root of the arithmetic mean of the squares of all deviations. Deviations being measured from arithmetic mean of the items.”
Standard Deviation is considered to be the best way of determining the dispersion of a data set. It is because standard deviation takes into account every value of a data set along with its algebraic signs. Standard Deviation can be calculated in three different series; viz., Individual, Discrete, and Frequency Distribution or Continuous Series.
What is Coefficient of Standard Deviation?
As Standard Deviation is an absolute measure of dispersion, one cannot use it for comparing the variability of two or more series when they are expressed in different units. Therefore, in order to compare the variability of two or more series with different units it is essential to determine the relative measure of Standard Deviation. Two of the relative measures of Standard Deviation are Coefficient of Standard Deviation and Coefficient of Variation.
Coefficient of Standard Deviation is a relative measure of Standard Deviation and is determined by dividing Standard Deviation by the Mean of the given data set. It is also known as the Standard Coefficient of Dispersion.
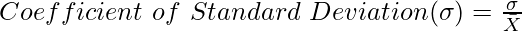
Properties of Standard Deviation
Some of the properties of Standard Deviation are as follows:
1. Independent of Change of Origin: Standard Deviation is independent of change of origin. It means that the value of standard deviation remains the same if a constant is added or subtracted from all observations in a series.
2. Standard Deviation of the Combined Series: Just like the arithmetic mean, one can determine the combined standard deviation of two or more groups.
3. Never less than Mean Deviation from Mean: For a given set of observations, the standard deviation of the series is never less than its mean deviation from the mean.
4. Affected by Change of Scale: Standard Deviation is affected by the change of scale. It means that if a constant is multiplied or divided to/by all of the observations, then the standard deviation will also get multiplied or divided by this constant.
5. Sum of the Square of the Deviations of the items from their Arithmetic Mean is Minimum: It means that the sum of the squares of deviations from the mean is always less than the sum of squares of deviations taken from the assumed mean.
Merits of Standard Deviation
The merits of Standard Deviation are:
1. Based on all Values: Every item of a series is considered in Standard Deviation. Therefore, a change in even one value of the series affects the value of standard deviation.
2. Algebraic Treatment: Further algebraic treatment is possible in case of standard deviation. For example, if one knows the standard deviation of different groups, their combined standard deviation can be easily determined.
3. Better Mathematical Process: The drawback of ignoring signs of deviations(as done in mean deviation) is removed in standard deviation through squaring of deviations.
4. Rigidly Defined: By far, standard deviation is the most essential and widely used measure of dispersion. It is a definite measure of dispersion; hence, is rigidly defined.
5. Less effect of Fluctuations in Sampling: If various independent samples are drawn from the same population, then we can see that the standard deviation of the distribution is least affected from one sample to another as compared to the effect caused by other measures of dispersion.
Demerits of Standard Deviation
The demerits of Standard Deviation are:
1. Difficult to Compute: As compared to other measures of dispersion, it is difficult to compute standard deviation.
2. Depend upon Units of Measurement: Standard Deviation of a series depends upon the units of measurement of the observations. Therefore, one cannot use standard deviation for comparing the dispersion of the distributions that are expressed in different units.
3. More Stress on Extreme Values: Standard Deviation gives more weightage to the extreme values and less weightage to the values which are nearer to mean.
Uses of Standard Deviation
1. One can use Standard Deviation to compare the dispersions of two or more given distributions when the units of measurement and arithmetic means of the distributions are the same.
2. Standard Deviation is also used for testing the reliability of mean. Simply put, the mean of a distribution which has the least standard deviation is considered more reliable.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...