Length of the transverse common tangent between the two non intersecting circles
Last Updated :
03 Aug, 2022
Given two circles of given radii, having there centres a given distance apart, such that the circles don’t touch each other. The task is to find the length of the transverse common tangent between the circles.
Examples:
Input: r1 = 4, r2 = 6, d = 12
Output: 6.63325
Input: r1 = 7, r2 = 9, d = 21
Output: 13.6015
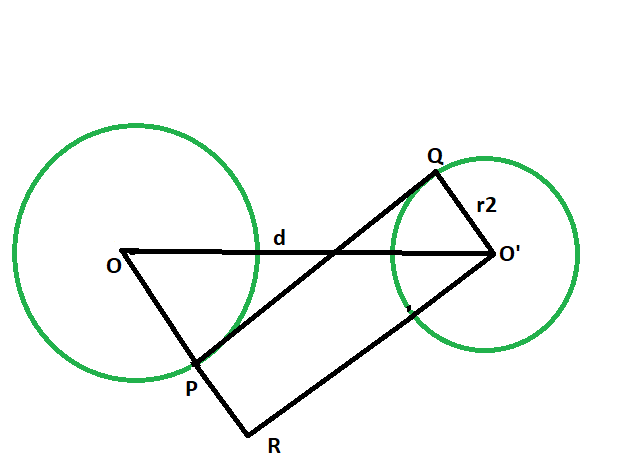
Approach:
- Let the radii of the circles be r1 & r2 respectively.
- Let the distance between the centers be d units.
- Draw a line O’R parallel to PQ,
- angle OPQ = angle RPQ = 90 deg
angle O’QP = 90 deg
{ line joining the center of the circle to the point of contact makes an angle of 90 degree with the tangent }
angle RPQ + angle O’QP = 180 deg
PR || O’Q
Since opposite sides are parallel and interior angles are 90, therefore O’PQR is a rectangle.- O’Q = RP = r2 and PQ = O’R
- In triangle OO’R
angle ORO’ = 90 deg
By Pythagoras theorem,
OR^2 + O’R^2 = OO’^2
O’R^2 = OO’^2 – OR^2
O’R^2 = d^2 – (r1+r2)^2
O’R^2 = √(d^2 – (r1+r2)^2)
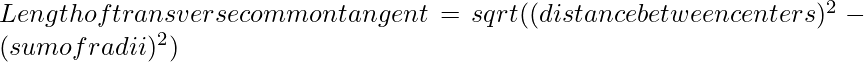
C++
#include <bits/stdc++.h>
using namespace std;
void lengthOfTangent(double r1, double r2, double d)
{
cout << "The length of the transverse"
<< " common tangent is "
<< sqrt(pow(d, 2) - pow((r1 + r2), 2))
<< endl;
}
int main()
{
double r1 = 4, r2 = 6, d = 12;
lengthOfTangent(r1, r2, d);
return 0;
}
|
Java
class GFG {
static void lengthOfTangent(double r1,
double r2, double d)
{
System.out.println("The length of the transverse"
+ " common tangent is "
+ Math.sqrt(Math.pow(d, 2)
- Math.pow((r1 + r2), 2)));
}
public static void main(String args[])
{
double r1 = 4, r2 = 6, d = 12;
lengthOfTangent(r1, r2, d);
}
}
|
Python3
from math import sqrt, pow
def lengthOfTangent(r1, r2, d):
print("The length of the transverse",
"common tangent is",
'{0:.6g}'.format(sqrt(pow(d, 2) -
pow((r1 + r2), 2))))
if __name__ == '__main__':
r1 = 4
r2 = 6
d = 12
lengthOfTangent(r1, r2, d)
|
C#
using System;
class GFG {
static void lengthOfTangent(double r1,
double r2, double d)
{
Console.WriteLine("The length of the transverse"
+ " common tangent is "
+ Math.Sqrt(Math.Pow(d, 2)
- Math.Pow((r1 + r2), 2)));
}
static public void Main()
{
double r1 = 4, r2 = 6, d = 12;
lengthOfTangent(r1, r2, d);
}
}
|
PHP
<?php
function lengthOfTangent($r1, $r2, $d)
{
echo "The length of the transverse common tangent is ",
sqrt(pow($d, 2) - pow(($r1 + $r2), 2)) ;
}
$r1 = 4; $r2 = 6; $d = 12;
lengthOfTangent($r1, $r2, $d);
?>
|
Javascript
<script>
function lengthOfTangent(r1,r2 , d)
{
document.write("The length of the transverse"
+ " common tangent is "
+ Math.sqrt(Math.pow(d, 2)
- Math.pow((r1 + r2), 2)));
}
var r1 = 4, r2 = 6, d = 12;
lengthOfTangent(r1, r2, d);
</script>
|
Output: The length of the transverse common tangent is 6.63325
Time Complexity: O(logn) because using inbuilt sqrt and pow function
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...