Length of the direct common tangent between two externally touching circles

Given two circles, of given radii, that touch each other externally. The task is to find the length of the direct common tangent between the circles.
Examples:

Input: r1 = 5, r2 = 9
Output: 13.4164

Input: r1 = 11, r2 = 13
Output: 23.9165

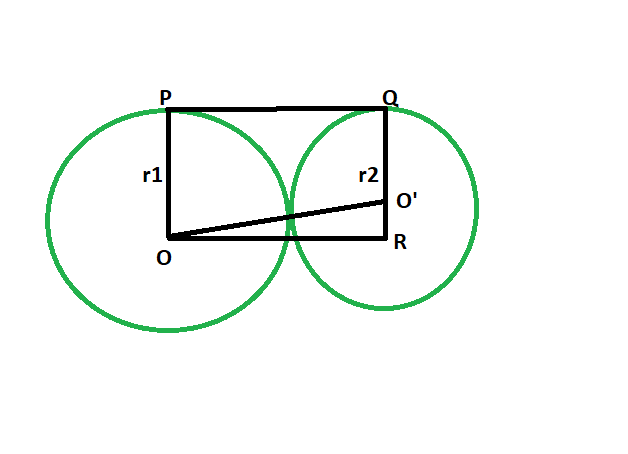
Approach

• Let the radii be r1 & r2 respectively.
• Draw a line OR parallel to PQ
• angle OPQ = 90 deg 
  angle O’QP = 90 deg
  { line joining the centre of the circle to the point of contact makes an angle of 90 degrees with the tangent }
• angle OPQ + angle O’QP = 180 
  OP || QR
• Since opposite sides are parallel and interior angles are 90, therefore OPQR is a rectangle.
• So OP = QR = r1 and PQ = OR = r1+r2
• In triangle OO’R
  angle ORO’ = 90
  By Pythagoras theorem
  OR^2 + O’R^2 = OO’^2 
  OO’^2 = (r1+r2)^2 + (r1-r2)^2
• So, OO’ = 2√(r1*r2)
  
  

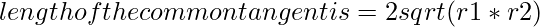
Below is the implementation of the above approach: 

C++

// C++ program to find the length of the direct
// common tangent between two circles
// which externally touch each other

#include <bits/stdc++.h>
using namespace std;

// Function to find the length
// of the direct common tangent
void lengtang(double r1, double r2)
{
    cout << "The length of the "
         << "direct common tangent is "
         << 2 * sqrt(r1 * r2) << endl;
}

// Driver code
int main()
{
    double r1 = 5, r2 = 9;
    lengtang(r1, r2);
    return 0;
}

Java

// Java program to find the length of the direct
// common tangent between two circles
// which externally touch each other
class GFG
{

    // Function to find the length
    // of the direct common tangent
    static void lengtang(double r1, double r2)
    {
        System.out.println("The length of the "
                + "direct common tangent is "
                + (2 * Math.sqrt(r1 * r2)));
    }

    // Driver code
    public static void main(String[] args)
    {
        double r1 = 5, r2 = 9;
        lengtang(r1, r2);
    }
}

// This code contributed by Rajput-Ji

Python3

# Python3 program to find the length
# of the direct common tangent
# between two circles which
# externally touch each other

# Function to find the length
# of the direct common tangent
def lengtang(r1, r2):
    print("The length of the direct",
                 "common tangent is",
             2 * (r1 * r2)**(1 / 2));

# Driver code
r1 = 5; r2 = 9;
lengtang(r1, r2);

# This code contributed
# by PrinciRaj1992

C#

// C# program to find the length of the direct
// common tangent between two circles
// which externally touch each other
using System;

class GFG
{
    // Function to find the length
    // of the direct common tangent
    static void lengtang(double r1, double r2)
    {
        Console.WriteLine("The length of the "
                + "direct common tangent is "
                + (2 * Math.Sqrt(r1 * r2)));
    }

    // Driver code
    static public void Main ()
    {
        double r1 = 5, r2 = 9;
        lengtang(r1, r2);
    }
}

// This code contributed by ajit.

PHP

<?php
// PHP program to find the length of the direct
// common tangent between two circles
// which externally touch each other

// Function to find the length
// of the direct common tangent
function lengtang($r1, $r2)
{
    echo "The length of the "
        , "direct common tangent is "
        , 2 * sqrt($r1 * $r2) ;
}

// Driver code
$r1 = 5; $r2 = 9;
lengtang($r1, $r2);

// This code is contributed by AnkitRai01

?>

Javascript

<script>

// javascript program to find the length of the direct
// common tangent between two circles
// which externally touch each other

// Function to find the length
// of the direct common tangent
function lengtang(r1 , r2)
{
    document.write("The length of the "
            + "direct common tangent is "
            + (2 * Math.sqrt(r1 * r2)).toFixed(5));
}

// Driver code
var r1 = 5, r2 = 9;
lengtang(r1, r2);

// This code contributed by Princi Singh

</script>

Output:

The length of the direct common tangent is 13.4164

Time Complexity: O(log(n)) because using inbuilt sqrt function

Auxiliary Space:  O(1)