Radius of the inscribed circle within three tangent circles

Last Updated : 07 Aug, 2022

There are 4 circles with positive integer radius r1, r2, r3 and r4 as shown in the figure below.

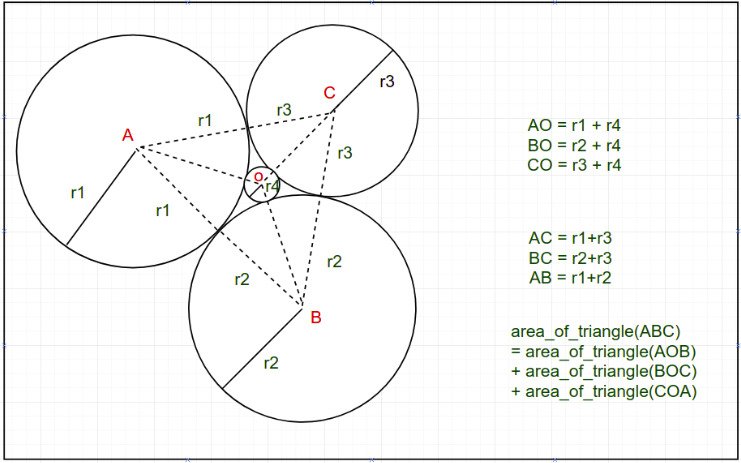
The task is to find the radius r4 of the circle formed by three circles when radius r1, r2, r3 are given.
(Note that the circles in the picture above are tangent to each other.)

Examples:

Input: r1 = 1, r2 = 1, r3 = 1
Output: 0.154701

Input: r1 = 23, r2 = 46, r3 = 69
Output: 6.000000

Approach 1: (Using Binary Search) :

The policy is to join the centers of all the circles and form 4 triangles
After the triangles are formed, equate the sum of areas of the three smaller triangles with the main triangle as far as possible using binary search.

Analysis of the mentioned approach:

This method works because initially there are 4 triangles as pointed in the above image.
The main triangle with sides $(r1+r2, r1+r3, r2+r3)$ and the three smaller triangles with sides $(r1+r4, r2+r4, r1+r2), (r1+r4, r3+r4, r1+r3), (r2+r4, r3+r4, r2+r3)$ .
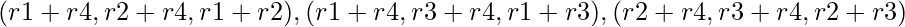The main triangle consists of the small ones so the area of the main triangle is the sum of the areas of the smaller ones.

Forming a search space:
Here binary search. The value for r can be chosen and the sum of the areas of all three smaller triangles can be computed and compared with the area of the main triangle.

Choosing lower bound $l = 0$
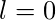
Choosing upper bound $h = s/(r1 + r2 + r3)$

By intuition, the upper bound value for r4 as the radius of the inscribed circle into the $(r1+r2, r1+r3, r2+r3)$ triangle is less than:
r_{upper_bound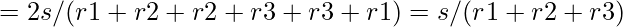} $= 2s/(r1+r2+r2+r3+r3+r1) = s/(r1+r2+r3)$
Now Binary Search can be applied at the following search space.

Below is the implementation of the problem using the above approach.

C++

// C++ implementation of the approach
#include <bits/stdc++.h>
using namespace std;
 
// Radius of the 3 given circles
// declared as double.
double r1, r2, r3;
 
// Calculation of area of a triangle by Heron's formula
double area(double a, double b, double c)
{
    double p = (a + b + c) / 2;
    return sqrt(p) * sqrt(p - a) * sqrt(p - b) * sqrt(p - c);
}
 
// Applying binary search to find the
// radius r4 of the required circle
double binary_search()
{
    // Area of main triangle
    double s = area(r1 + r2, r2 + r3, r3 + r1);
    double l = 0, h = s / (r1 + r2 + r3);
    // Loop runs until l and h becomes approximately equal
    while (h - l >= 1.e-7) {
        double mid = (l + h) / 2;
 
        // Area of smaller triangles
        double s1 = area(mid + r1, mid + r2, r1 + r2);
        double s2 = area(mid + r1, mid + r3, r1 + r3);
        double s3 = area(mid + r2, mid + r3, r2 + r3);
 
        // If sum of smaller triangles
        // is less than main triangle
        if (s1 + s2 + s3 < s) {
            l = mid;
        }
        // If sum of smaller triangles is
        // greater than or equal to main triangle
        else {
            h = mid;
        }
    }
    return (l + h) / 2;
}
// Driver code
int main()
{
    // Taking r1, r2, r3 as input
    r1 = 1.0;
    r2 = 2.0;
    r3 = 3.0;
    // Call to function binary search
    cout << fixed << setprecision(6) << binary_search() << endl;
    return 0;
}

Java

// Java implementation of the approach
import java.util.*;
 
class GFG
{
 
    // Radius of the 3 given circles
    // declared as double.
    static double r1, r2, r3;
 
    // Calculation of area of a triangle by Heron's formula
    static double area(double a, double b, double c) 
    {
        double p = (a + b + c) / 2;
        return Math.sqrt(p) * Math.sqrt(p - a) * 
               Math.sqrt(p - b) * Math.sqrt(p - c);
    }
 
    // Applying binary search to find the
    // radius r4 of the required circle
    static double binary_search()
    {
        // Area of main triangle
        double s = area(r1 + r2, r2 + r3, r3 + r1);
        double l = 0, h = s / (r1 + r2 + r3);
         
        // Loop runs until l and h becomes approximately equal
        while (h - l >= 1.e-7)
        {
            double mid = (l + h) / 2;
 
            // Area of smaller triangles
            double s1 = area(mid + r1, mid + r2, r1 + r2);
            double s2 = area(mid + r1, mid + r3, r1 + r3);
            double s3 = area(mid + r2, mid + r3, r2 + r3);
 
            // If sum of smaller triangles
            // is less than main triangle
            if (s1 + s2 + s3 < s) 
            {
                l = mid;
            }
             
            // If sum of smaller triangles is
            // greater than or equal to main triangle
            else
            {
                h = mid;
            }
        }
        return (l + h) / 2;
    }
 
    // Driver code
    public static void main(String[] args)
    {
        // Taking r1, r2, r3 as input
        r1 = 1.0;
        r2 = 2.0;
        r3 = 3.0;
         
        // Call to function binary search
        System.out.printf("%.6f", binary_search());
    }
}
 
// This code is contributed by 29AjayKumar

Python3

# Python3 implementation of the approach 
import math
 
# Radius of the 3 given circles 
r1 = 0
r2 = 0
r3 = 0
 
# Calculation of area of a 
# triangle by Heron's formula 
def area(a, b, c):
     
    p = (a + b + c) / 2
 
    return ((math.sqrt(p)) *
            (math.sqrt(p - a)) *
            (math.sqrt(p - b)) *
            (math.sqrt(p - c)))
 
# Applying binary search to find the 
# radius r4 of the required circle 
def binary_search():
     
    global r1, r2, r3
 
    # Area of main triangle 
    s = area(r1 + r2, r2 + r3, r3 + r1)
    l = 0
    h = s / (r1 + r2 + r3)
 
    # Loop runs until l and h 
    # becomes approximately equal 
    while (h - l > 0.00000001):
        mid = (l + h) / 2
 
        # Area of smaller triangles
        s1 = area(mid + r1, mid + r2, r1 + r2)
        s2 = area(mid + r1, mid + r3, r1 + r3)
        s3 = area(mid + r2, mid + r3, r2 + r3)
 
        # If sum of smaller triangles 
        # is less than main triangle 
        if (s1 + s2 + s3 < s):
            l = mid
             
        # If sum of smaller triangles is 
        # greater than or equal to main triangle 
        else:
            h = mid
             
    return ((l + h) / 2)
 
# Driver code 
 
# Taking r1, r2, r3 as input 
r1 = 1
r2 = 2
r3 = 3
 
# Call to function binary search 
print("{0:.6f}".format(binary_search()))
 
# This code is contributed by avanitrachhadiya2155

C#

// C# implementation of the approach
using System;
 
class GFG
{
 
    // Radius of the 3 given circles
    // declared as double.
    static double r1, r2, r3;
 
    // Calculation of area of a triangle by Heron's formula
    static double area(double a, double b, double c) 
    {
        double p = (a + b + c) / 2;
        return Math.Sqrt(p) * Math.Sqrt(p - a) * 
            Math.Sqrt(p - b) * Math.Sqrt(p - c);
    }
 
    // Applying binary search to find the
    // radius r4 of the required circle
    static double binary_search()
    {
        // Area of main triangle
        double s = area(r1 + r2, r2 + r3, r3 + r1);
        double l = 0, h = s / (r1 + r2 + r3);
         
        // Loop runs until l and h 
        // becomes approximately equal
        while (h - l > 0.00000001)
        {
            double mid = (l + h) / 2;
 
            // Area of smaller triangles
            double s1 = area(mid + r1, mid + r2, r1 + r2);
            double s2 = area(mid + r1, mid + r3, r1 + r3);
            double s3 = area(mid + r2, mid + r3, r2 + r3);
 
            // If sum of smaller triangles
            // is less than main triangle
            if (s1 + s2 + s3 < s) 
            {
                l = mid;
            }
             
            // If sum of smaller triangles is
            // greater than or equal to main triangle
            else
            {
                h = mid;
            }
        }
        return (l + h) / 2;
    }
 
    // Driver code
    public static void Main(String[] args)
    {
        // Taking r1, r2, r3 as input
        r1 = 1.0;
        r2 = 2.0;
        r3 = 3.0;
         
        // Call to function binary search
        Console.Write("{0:F6}", binary_search());
    }
}
 
// This code is contributed by Rajput-Ji

Javascript

<script>
 
// Javascript implementation of the approach
 
// Radius of the 3 given circles
// declared as double.
let r1, r2, r3;
 
// Calculation of area of a triangle
// by Heron's formula
function area(a, b, c)
{
    let p = (a + b + c) / 2;
    return Math.sqrt(p) * Math.sqrt(p - a) * 
       Math.sqrt(p - b) * Math.sqrt(p - c);
}
 
// Applying binary search to find the
// radius r4 of the required circle
function binary_search()
{
     
    // Area of main triangle
    let s = area(r1 + r2, r2 + r3, r3 + r1);
    let l = 0, h = s / (r1 + r2 + r3);
     
    // Loop runs until l and h
    // becomes approximately equal
    while (h - l >= 1.e-7)
    {
        let mid = (l + h) / 2;
 
        // Area of smaller triangles
        let s1 = area(mid + r1, mid + r2, r1 + r2);
        let s2 = area(mid + r1, mid + r3, r1 + r3);
        let s3 = area(mid + r2, mid + r3, r2 + r3);
 
        // If sum of smaller triangles
        // is less than main triangle
        if (s1 + s2 + s3 < s) 
        {
            l = mid;
        }
         
        // If sum of smaller triangles is
        // greater than or equal to main triangle
        else
        {
            h = mid;
        }
    }
    return (l + h) / 2;
}
 
// Driver code
 
// Taking r1, r2, r3 as input
r1 = 1.0;
r2 = 2.0;
r3 = 3.0;
 
// Call to function binary search
document.write(binary_search().toPrecision(6));
 
// This code is contributed by subhammahato348
 
</script>

Output:

0.260870

Time Complexity: O(logn)

Auxiliary Space: O(1)

Approach 2: (Using Descartes’ Theorem)

According to Descartes’ Theorem, the reciprocals of radii, or “curvatures”, of these circles 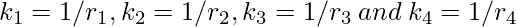$k_1 = 1/r_1, k_2 = 1/r_2, k_3 = 1/r_3\:and\:k_4 = 1/r_4$ satisfy the following relation.
$2(k_1^2+k_2^2+k_3^2+k_4^2) = (k_1+k_2+k_3+k_4)^2$
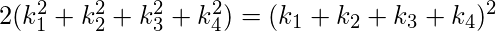
If 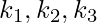$k_1, k_2, k_3$ are known, one can solve for,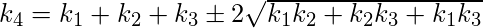 $k_4 = k_1 + k_2 + k_3 \pm 2\sqrt{k_1 k_2 + k_2 k_3 + k_1 k_3}$
On solving the above equation;
$r_4 = (r_1*r_2*r_3)\, /\, (r_1*r_2 + r_2*r_3 + r_3*r_1 + 2.0\, *\, \sqrt{(r_1*r_2*r_3*(r_1+r_2+r_3))})$

Below is the implementation of the problem using the above formula.

C++

// C++ implementation of the approach
#include <bits/stdc++.h>
using namespace std;
 
// Driver code
int main()
{
    // Radius of the 3 given circles declared as double.
    double r1, r2, r3;
 
    // Taking r1, r2, r3 as input
    r1 = 1;
    r2 = 2;
    r3 = 3;
 
    // Calculation of r4 using formula given above
    double r4 = (r1 * r2 * r3)
                / (r1 * r2 + r2 * r3 + r1 * r3
                   + 2.0 * sqrt(r1 * r2 * r3 * (r1 + r2 + r3)));
    cout << fixed << setprecision(6) << r4 << '\n';
    return 0;
}

Java

// Java implementation of the approach
class GFG 
{
 
    // Driver code
    public static void main(String[] args) 
    {
        // Radius of the 3 given circles declared as double.
        double r1, r2, r3;
 
        // Taking r1, r2, r3 as input
        r1 = 1;
        r2 = 2;
        r3 = 3;
 
        // Calculation of r4 using formula given above
        double r4 = (r1 * r2 * r3) / 
                    (r1 * r2 + r2 * r3 + r1 * r3 + 2.0 * 
                    Math.sqrt(r1 * r2 * r3 * (r1 + r2 + r3)));
        System.out.printf("%.6f", r4);
    }
}
 
// This code is contributed by 29AjayKumar

Python3

# Python3 implementation of the approach
from math import sqrt
 
# Driver code
 
# Radius of the 3 given circles declared as double.
 
# Taking r1, r2, r3 as input
r1 = 1
r2 = 2
r3 = 3
 
# Calculation of r4 using formula given above
r4 = (r1 * r2 * r3)/ (r1 * r2 + r2 * r3 + r1 * r3
            + 2.0 * sqrt(r1 * r2 * r3 * (r1 + r2 + r3)))
print(round(r4, 6))
 
# This code is contributed by mohit kumar 29

C#

// C# implementation of the approach
using System;
 
class GFG 
{
  
    // Driver code
    public static void Main(String[] args) 
    {
        // Radius of the 3 given circles declared as double.
        double r1, r2, r3;
  
        // Taking r1, r2, r3 as input
        r1 = 1;
        r2 = 2;
        r3 = 3;
  
        // Calculation of r4 using formula given above
        double r4 = (r1 * r2 * r3) / 
                    (r1 * r2 + r2 * r3 + r1 * r3 + 2.0 * 
                    Math.Sqrt(r1 * r2 * r3 * (r1 + r2 + r3)));
        Console.Write("{0:F6}", r4);
    }
}
 
// This code contributed by PrinciRaj1992

Javascript

<script>
 
// Javascript implementation of the approach
 
// Driver code
 
// Radius of the 3 given circles 
// declared as double.
let r1, r2, r3;
 
// Taking r1, r2, r3 as input
r1 = 1;
r2 = 2;
r3 = 3;
 
// Calculation of r4 using formula given above
let r4 = (r1 * r2 * r3) / (r1 * r2 + r2 * 
          r3 + r1 * r3 + 2.0 * Math.sqrt(
          r1 * r2 * r3 * (r1 + r2 + r3)));
 
document.write(r4.toFixed(6) + "<br>");
 
// This code is contributed by souravmahato348
 
</script>

Output:

0.260870

Time Complexity: O(log(n)) as inbuilt sqrt function is being used which has time complexity of log(n)

Auxiliary Space: O(1)

Reference :

Suggest improvement

Multiply Large Numbers using Grid Method

Prime Numbers present at Kth level of a Binary Tree

Share your thoughts in the comments

Radius of the inscribed circle within three tangent circles

C++

Java

Python3

C#

Javascript

C++

Java

Python3

C#

Javascript

Please Login to comment...

Similar Reads

What kind of Experience do you want to share?