Ratio of the distance between the centers of the circles and the point of intersection of two transverse common tangents to the circles
Last Updated :
31 May, 2022
Given two circles, of given radii, such that the circles don’t touch each other. The task is to find the ratio of the distance between the centres of the circles and the point of intersection of two transverse common tangents to the circles.
Examples:
Input :r1 = 4, r2 = 8
Output :1:2
Input :r1 = 5, r2 = 13
Output :5:13

Approach:
- Let the radii of the circles be r1 & r2 and C1 & C2 respectively.
- Let P be the point of intersection of two transverse common tangents to the circles, and A1 & A2 be the point of contact of the tangents with the circles.
- In triangle PC1A1 & triangle PC2A2,
angle C1A1P = angle C2A2P = 90 deg { line joining the centre of the circle to the point of contact makes an angle of 90 degree with the tangent },
also, angle A1PC1 = angle A2PC2{vertically opposite angles are always equal}
so, angle A1C1P = angle A2C2P
as angles are same, triangles PC1A1 & PC2A2 are similar. - So, due to similarity of the triangles,
C1P/C2P = C1A1/C2A2 = r1/r2
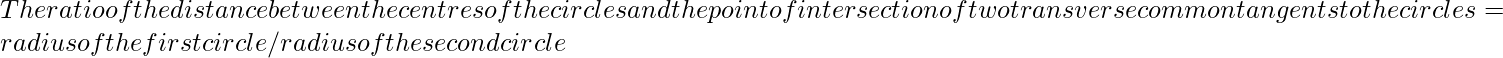
C++
#include <bits/stdc++.h>
using namespace std;
int GCD(int a, int b)
{
return (b != 0 ? GCD(b, a % b) : a);
}
void ratiotang(int r1, int r2)
{
cout << "The ratio is "
<< r1 / GCD(r1, r2)
<< ":"
<< r2 / GCD(r1, r2)
<< endl;
}
int main()
{
int r1 = 4, r2 = 8;
ratiotang(r1, r2);
return 0;
}
|
Java
import java.io.*;
class GFG{
static int GCD(int a, int b)
{
return (b != 0 ? GCD(b, a % b) : a);
}
static void ratiotang(int r1, int r2)
{
System.out.println("The ratio is "
+ r1 / GCD(r1, r2)
+ ":"
+ r2 / GCD(r1, r2));
}
public static void main (String[] args)
{
int r1 = 4, r2 = 8;
ratiotang(r1, r2);
}
}
|
Python
def GCD(a, b):
if(b!=0):
return GCD(b, a%b);
else:
return a;
def ratiotang(r1, r2):
print("The ratio is", r1 // GCD(r1, r2),
":", r2 // GCD(r1, r2));
r1 = 4; r2 = 8;
ratiotang(r1, r2);
|
C#
using System;
class GFG
{
static int GCD(int a, int b)
{
return (b != 0 ? GCD(b, a % b) : a);
}
static void ratiotang(int r1, int r2)
{
Console.WriteLine("The ratio is "
+ r1 / GCD(r1, r2)
+ ":"
+ r2 / GCD(r1, r2));
}
static public void Main ()
{
int r1 = 4, r2 = 8;
ratiotang(r1, r2);
}
}
|
PHP
<?php
function GCD($a, $b)
{
return ($b != 0 ? GCD($b, $a % $b) : $a);
}
function ratiotang($r1, $r2)
{
echo "The ratio is ", $r1 / GCD($r1, $r2),
":", $r2 / GCD($r1, $r2);
}
$r1 = 4;
$r2 = 8;
ratiotang($r1, $r2);
?>
|
Javascript
<script>
function GCD(a , b)
{
return (b != 0 ? GCD(b, a % b) : a);
}
function ratiotang(r1 , r2)
{
document.write("The ratio is "
+ r1 / GCD(r1, r2)
+ ":"
+ r2 / GCD(r1, r2));
}
var r1 = 4, r2 = 8;
ratiotang(r1, r2);
</script>
|
Time Complexity: O(log(min(a, b)))
Auxiliary Space: O(log(min(a, b)))
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...