Find the radius of the circles which are lined in a row, and distance between the centers of first and last circle is given
Last Updated :
31 May, 2022
Given here are n circles which touch each other externally, and are lined up in a row. The distance between the centers of the first and last circle is given. The circles have a radius of equal length. The task is to find the radius of each circle.
Examples:
Input: d = 42, n = 4
Output: The radius of each circle is 7
Input: d = 64, n = 5
Output: The radius of each circle is 8

Approach:
Suppose there are n circles each having radius of length r.
Let, the distance between the first and last circles = d
From the figure, it is clear,
r + r + (n-2)*2r = d
2r + 2nr – 4r = d
2nr – 2r = d
so, r = d/(2n-2)
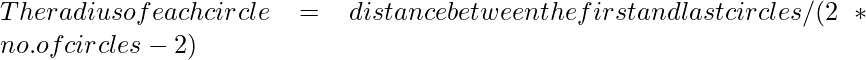
C++
#include <bits/stdc++.h>
using namespace std;
void radius(int n, int d)
{
cout << "The radius of each circle is "
<< d / (2 * n - 2) << endl;
}
int main()
{
int d = 42, n = 4;
radius(n, d);
return 0;
}
|
Java
import java.io.*;
class GFG
{
static void radius(int n, int d)
{
System.out.print( "The radius of each circle is "
+d / (2 * n - 2));
}
static public void main (String []args)
{
int d = 42, n = 4;
radius(n, d);
}
}
|
Python3
def radius(n, d):
print("The radius of each circle is ",
d / (2 * n - 2));
d = 42; n = 4;
radius(n, d);
|
C#
using System;
class GFG
{
static void radius(int n, int d)
{
Console.Write( "The radius of each circle is "
+d / (2 * n - 2));
}
static public void Main ()
{
int d = 42, n = 4;
radius(n, d);
}
}
|
Javascript
<script>
function radius(n , d)
{
document.write( "The radius of each circle is "
+d / (2 * n - 2));
}
var d = 42, n = 4;
radius(n, d);
</script>
|
Output: The radius of each circle is 7
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...