Angle of intersection of two circles having their centers D distance apart
Last Updated :
16 Jul, 2021
Given two positive integers R1 and R2 representing the radius of two intersecting circles having a distance D between their centers, the task is to find the cosine of the angle of intersection between the two circles.
Examples:
Input: R1 = 3, R2 = 4, D = 5
Output: 0
Input: R1 = 7, R2 = 3, D = 6
Output: 0.52381
Approach: The given problem can be solved by using the Geometric Algorithm as illustrated below:
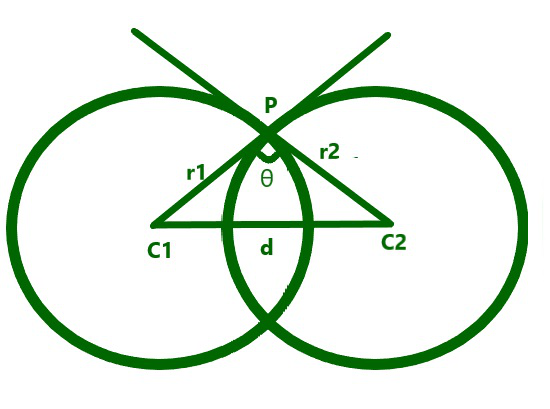
From the above image and using the Pythagoras Theorem, the cosine of the angle of intersection of the two circles can be found using the formula:
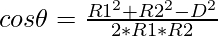
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
float angle(float R1, float R2, float D)
{
float ans = (R1 * R1 + R2 * R2 - D * D)
/ (2 * R1 * R2);
return ans;
}
int main()
{
float R1 = 3, R2 = 4;
float D = 5;
cout << angle(R1, R2, D);
return 0;
}
|
Java
import java.io.*;
class GFG{
static float angle(float R1, float R2, float D)
{
float ans = (R1 * R1 + R2 * R2 - D * D) /
(2 * R1 * R2);
return ans;
}
public static void main (String[] args)
{
float R1 = 3, R2 = 4;
float D = 5;
System.out.println(angle(R1, R2, D));
}
}
|
Python3
def angle(R1, R2, D):
ans = ((R1 * R1 + R2 * R2 - D * D) /
(2 * R1 * R2))
return ans
if __name__ == '__main__':
R1 = 3
R2 = 4
D = 5
print(angle(R1, R2, D))
|
C#
using System;
class GFG{
static float angle(float R1, float R2, float D)
{
float ans = (R1 * R1 + R2 * R2 - D * D) /
(2 * R1 * R2);
return ans;
}
public static void Main(string[] args)
{
float R1 = 3, R2 = 4;
float D = 5;
Console.Write(angle(R1, R2, D));
}
}
|
Javascript
<script>
function angle(R1, R2, D)
{
var ans = (R1 * R1 + R2 * R2 - D * D) /
(2 * R1 * R2);
return ans;
}
var R1 = 3, R2 = 4;
var D = 5;
document.write(angle(R1, R2, D));
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...