Equation of circle from center and radius

Given the center of circle (x1, y1) and its radius r, find the equation of the circle having center (x1, y1) and having radius r.
Examples:

Input : x1 = 2, y1 = -3, r = 8
Output : x^2 + y^2 – 4*x + 6*y = 51.
Input : x1 = 0, y1 = 0, r = 2
Output : x^2 + y^2 – 0*x + 0*y = 4.

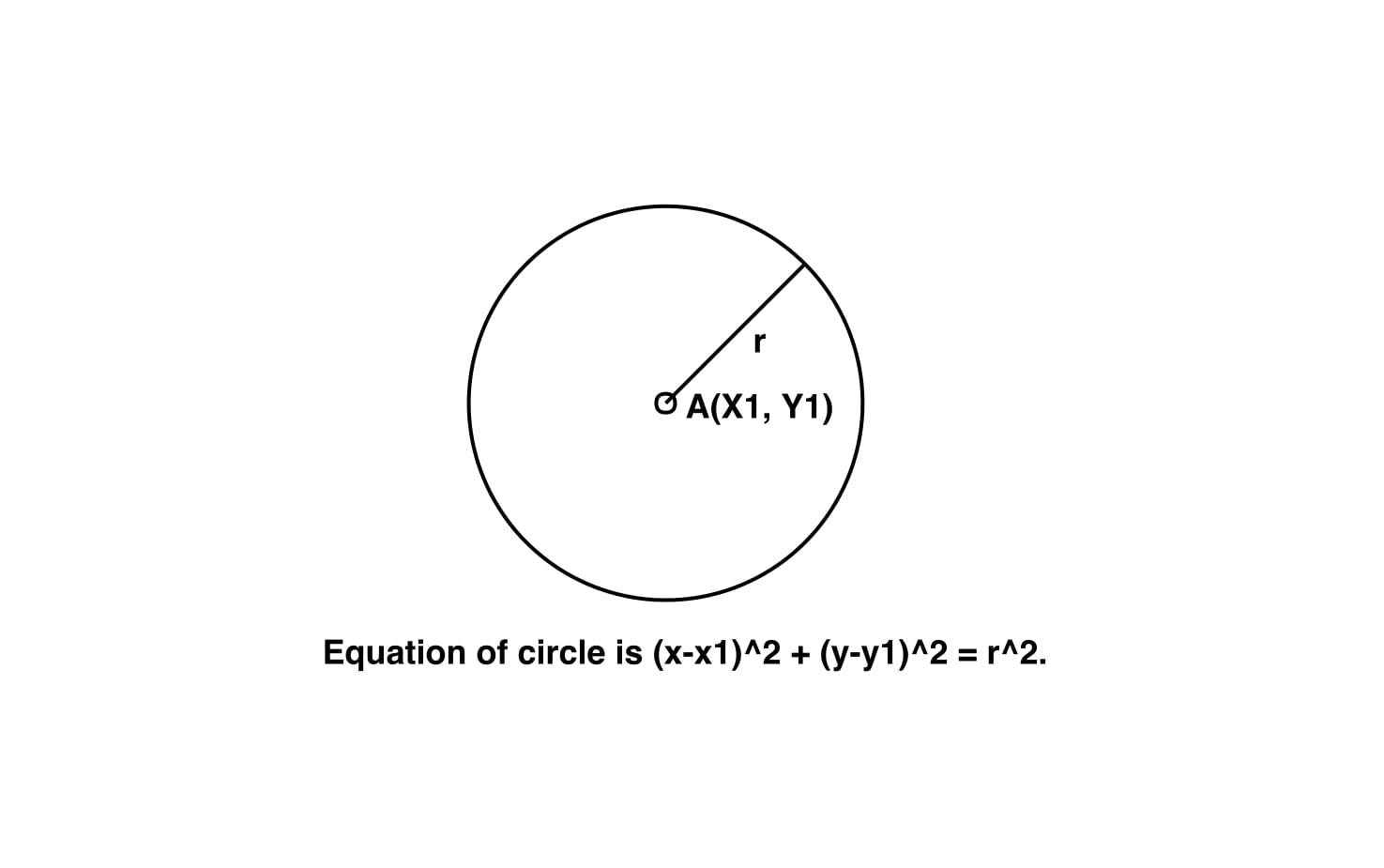
Approach:
Given the center of circle (x1, y1) and its radius r, we have to find the equation of the circle having center (x1, y1) and having radius r.
the equation of circle having center (x1, y1) and having radius r is given by :-

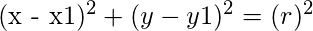
on expanding above equation

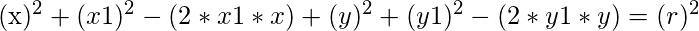
on arranging above we get

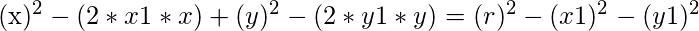
Below is the implementation of above approach:

C++

// CPP program to find the equation
// of circle.
#include <iostream>
using namespace std;
 
// Function to find the equation of circle
void circle_equation(double x1, double y1, double r)
{
    double a = -2 * x1;
 
    double b = -2 * y1;
 
    double c = (r * r) - (x1 * x1) - (y1 * y1);
 
    // Printing result
    cout << "x^2 + (" << a << " x) + ";
    cout << "y^2 + (" << b << " y) = ";
    cout << c << "." << endl;
}
 
// Driver code
int main()
{
    double x1 = 2, y1 = -3, r = 8;
    circle_equation(x1, y1, r);
    return 0;
}

Java

// Java program to find the equation
// of circle.
import java.util.*;
 
class solution
{
 
 // Function to find the equation of circle
static void circle_equation(double x1, double y1, double r)
{
    double a = -2 * x1;
 
    double b = -2 * y1;
 
    double c = (r * r) - (x1 * x1) - (y1 * y1);
 
    // Printing result
    System.out.print("x^2 + (" +a+ " x) + ");
     System.out.print("y^2 + ("+b + " y) = ");
     System.out.println(c +"." );
}
 
// Driver code
public static void main(String arr[])
{
    double x1 = 2, y1 = -3, r = 8;
    circle_equation(x1, y1, r);
  
}
 
}

Python3

# Python3 program to find the
# equation of circle.
 
# Function to find the
# equation of circle
def circle_equation(x1, y1, r):
    a = -2 * x1;
 
    b = -2 * y1;
 
    c = (r * r) - (x1 * x1) - (y1 * y1);
 
    # Printing result
    print("x^2 + (", a, "x) + ", end = "");
    print("y^2 + (", b, "y) = ", end = "");
    print(c, ".");
 
# Driver code
x1 = 2;
y1 = -3;
r = 8;
circle_equation(x1, y1, r);
 
# This code is contributed
# by mits

C#

// C# program to find the equation
// of circle.
using System;
 
class GFG
{
 
// Function to find the equation of circle
public static void circle_equation(double x1,
                                   double y1,
                                   double r)
{
    double a = -2 * x1;
 
    double b = -2 * y1;
 
    double c = (r * r) - (x1 * x1) - (y1 * y1);
 
    // Printing result
    Console.Write("x^2 + (" + a + " x) + ");
    Console.Write("y^2 + ("+ b + " y) = ");
    Console.WriteLine(c + "." );
}
 
// Driver code
public static void Main(string []arr)
{
    double x1 = 2, y1 = -3, r = 8;
    circle_equation(x1, y1, r);
}
}
 
// This code is contributed
// by SoumkMondal

PHP

<?php
// PHP program to find the equation
// of circle.
 
// Function to find the
// equation of circle
function circle_equation($x1, $y1, $r)
{
    $a = -2 * $x1;
 
    $b = -2 * $y1;
 
    $c = ($r * $r) - ($x1 * $x1) -
                     ($y1 * $y1);
 
    // Printing result
    echo "x^2 + (" . $a . " x) + ";
    echo "y^2 + (" . $b . " y) = ";
    echo $c . "." . "\n";
}
 
// Driver code
$x1 = 2; $y1 = -3; $r = 8;
circle_equation($x1, $y1, $r);
 
// This code is contributed
// by Akanksha Rai
?>

Javascript

<script>
// java script  program to find the equation
// of circle.
 
// Function to find the
// equation of circle
function circle_equation(x1, y1, r)
{
    let a = -2 * x1;
 
    let b = -2 * y1;
 
    let c = (r * r) - (x1 * x1) -
                    (y1 * y1);
 
    // Printing result
    document.write( "x^2 + (" +a + " x) + ");
    document.write( "y^2 + (" +b+ " y) = ");
    document.write( c+ "<br>");
}
 
// Driver code
let x1 = 2;
let y1 = -3;
let r = 8;
circle_equation(x1, y1, r);
 
// This code is contributed by sravan kumar
</script>