Ellipse Formula

Last Updated : 24 Jan, 2024

Conic Sections are the figures or curves which are generated from the sections of the cone. Different curves are generated when we cut the cone with a plane at different angles. Ellipse is also a part of conic sections. Other conic sections include – circles, parabola, hyperbola, etc. We encounter ellipse at a lot of places in our lives, for example – A rugby ball or an egg is in an oval shape, which when projected to 2d give us an ellipse. Planetary motion is also another example of the ellipse. Planets revolve around the sun in the form of an ellipse. It is essential for us to study ellipse to be able to work on these problems. Let’s introduce the ellipse and see its properties in detail.

Introduction to Ellipse

An ellipse is a set of points in a plane, the sum of whose distances from two fixed points in the plane is constant. The two fixed points are called foci of the ellipse. The figure below shows the two fixed points and shows how an ellipse can be traced from those points.

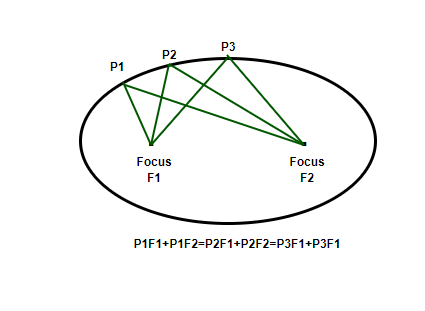
A₁F₁ + A₁F₂ = A₂F₁ + A₂F₂ = A₃F₁ + A₃F₂

Note: The constant distance that is mentioned above should always be less than the distance between the two focal points.

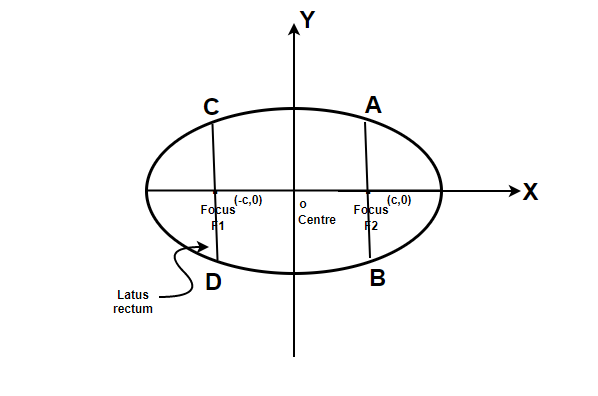
The figure below shows a labeled diagram of the ellipse.

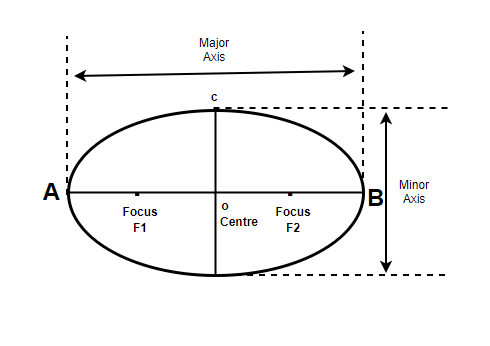
The line segment joining and going through two foci is called the major axis. The mid-point of the line segment between two foci is called the centre of the ellipse. The line perpendicular to the major axis and passing through the centre of the ellipse is called the minor axis. The endpoints of the major axis which cut the ellipse are called vertices of the ellipse.

Let’s say the length of the major axis is 2a and while that of the minor axis is 2b. The distance between two foci is defined as 2c. The diagram below demonstrates the axes and their lengths.

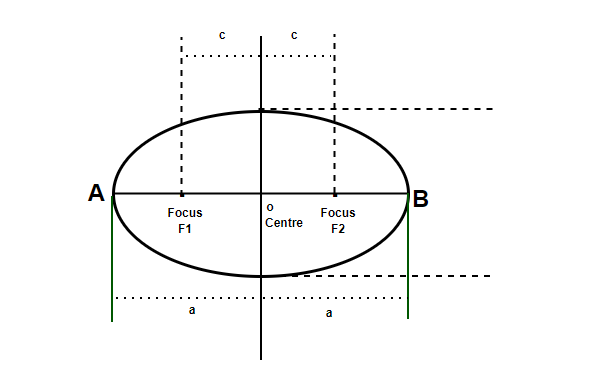
Further sections, introduce the properties and the equation of the ellipse.

Relationship between Major and Minor Axes

We have defined the major and minor axes in the previous sections. Now the question that comes to mind is that are they related to each other in some way? Are there any special cases of the ellipse? First, let’s establish the relationship between the major and the minor axes.

Consider point A. The distance of A from the two Centre is,

AF₁ + AF₂ = OF₁ + OA + AF₂

= c + a + a – c = 2a

From point B on the minor axis.

F₁B + F₂B = $2\sqrt{b^2 + c^2}$

We know from the definition of the ellipse that,

AF₁ + AF₂= F₁B + F₂B

$2a = 2\sqrt{b^2 + c^2}\\ a = \sqrt{b^2 + c^2}$

Eccentricity

The eccentricity of an ellipse is the ratio of the distances from the Centre of the ellipse to one of the foci and to one of the vertices of the ellipse

$e = \frac{c}{a}$

Equation of Ellipse

The figure below represents a standard ellipse, with F₁ and F₂ as foci and O as the mid-point of the line segment F₁F₂. Suppose there is a point on ellipse P(x, y). We know,

PF₁ + PF₂ = 2a

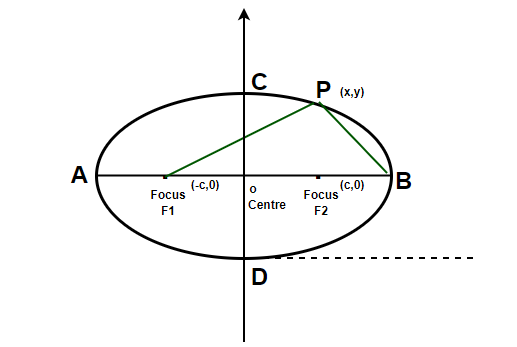
We will use the distance formula to substitute the values of BF_1,BF₂.

$\sqrt{(x +c)^2 + y^2} + \sqrt{(x-c)^2 + y^2} = 2a \\ \sqrt{(x +c)^2 + y^2} = 2a - \sqrt{(x-c)^2 + y^2}$

Squaring both sides,

(x +c)² + y² = 4a² + (x-c)² + y² + 2y(x-c)

x² + c²+ 2xc + y² = 4a² + x² + c² + -2xc + y² + 2xy – 2yc

Upon Simplification,

$\\ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$

The figures below represent the other possible cases for the ellipse.

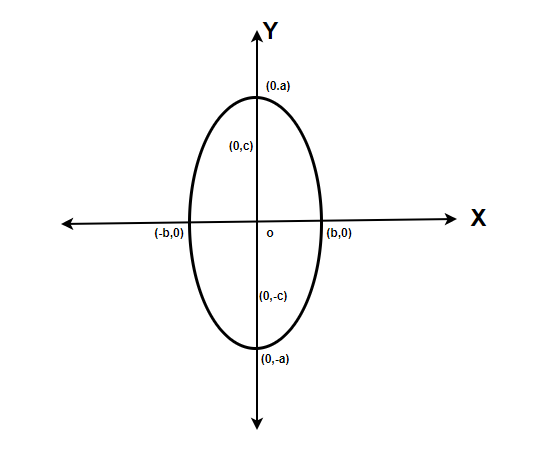
The equation for this ellipse will be,

$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$

Latus Rectum

This is a line segment that goes through both foci and is perpendicular to the major axis. Its ends lie at its intersection with the ellipse. Let the length of the AF₂be l.

Now the coordinates of A will be (c, l). Now we know that A lies on the ellipse, so it will satisfy the equation of the ellipse.

$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \\ \frac{c^2}{a^2} + \frac{l^2}{b^2} = 1 \\ \text{We know, c = ae} \\ e^2 + \frac{l^2}{b^2} = 1 \\ l^2 = b^2 (1 - e^2) \\ l = b\sqrt{1 - e^2}\\$

Sample Problems

Question 1: Find the equation of ellipse if the endpoints of the major axis lie on (-10,0) and (10,0) and endpoints of the minor axis lie on (0,-5) and (0,5).

Solution:

Since the major axis is x-axis, the ellipse equation should be,

$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$

2a = 20

⇒a = 10

2b = 10

⇒b = 5

$\frac{x^2}{10^2} + \frac{y^2}{5^2} = 1$

Question 2: Find the equation of an ellipse with origin as centre and x-axis as major axis. Given that the distance between two foci is 10cm, e = 0.4 and b = 4cm

Solution:

Standard equation of the ellipse is,

$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$

We know b = 4, e = 0.4 and c = 10.

$c = ae \\ 10 = a(0.4) \\ 25 = a$

Thus, now we have a = 25 and b = 4

So, the equation of ellipse is,

$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \\ \frac{x^2}{25^2} + \frac{y^2}{4^2} = 1$

Question 3: Find the equation of an ellipse whose major axis is 40cm and foci lie on (5,0) and (-5,0).

Solution:

$\frac{x^2}{a^2} + \frac{x^2}{b^2} = 1$

a = $\frac{40}{2} = 20$

We know c = 10

c² = a² – b²

10²= 20² – b²

b² = 20² – 10²

b² = 300

Thus, the equation becomes,

$\frac{x^2}{400} + \frac{x^2}{300} = 1$

Question 4: Find the equation of an ellipse whose major axis is 40cm and foci lie on (0,5) and (0,-5).

Solution:

Since the foci lie on y-axis. The major axis is on y-axis. Thus, the ellipse is of the form,

$\frac{x^2}{b^2} + \frac{x^2}{a^2} = 1$

a = $\frac{40}{2} = 20$

We know c = 10

c² = a² – b²

10²= 20² – b²

b² = 20² – 10²

b² = 300

Thus, the equation becomes,

$\frac{x^2}{300} + \frac{x^2}{400} = 1$

Question 5: Find the equation of ellipse if the major axis is the x-axis and the minor axis is the y-axis and (4,3) and (-1,4) lie on the ellipse.

Solution:

Standard equation of the ellipse is,

$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$

These points must satisfy the equation. (4,3) and (-1, 4).

$\frac{4^2}{a^2} + \frac{(-3)^2}{b^2} = 1 \\ \frac{16}{a^2} + \frac{9}{b^2} = 1 \\$

$\frac{(-1)^2}{a^2} + \frac{4^2}{b^2} = 1 \\ \frac{1}{a^2} + \frac{16}{b^2} = 1 \\$

Let’s say, $x = \frac{1}{a} \text{ and } y = \frac{1}{b}$

16x + 9b = 1

x + 16b = 1

Solving the equations,

We find that $a = \frac{247}{7} \text{ and } b = \frac{247}{15}$