Class 11 RD Sharma Solutions – Chapter 26 Ellipse – Exercise 26.1 | Set 2
Last Updated :
30 Jun, 2021
Question 11. Find the equation of the ellipse whose foci are at (±3, 0) and which passes through (4, 1).
Solution:
Let the equation of the ellipse be 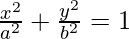 ….(i)
….(i)
Given that the ellipse whose foci are at (±3, 0) and which passes through (4, 1)
So,
ae = 3
(ae)2 = 9
y = 1 and x = 4
Substituting the values of x and y in the above equation, we have:
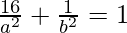 …(ii)
…(ii)
As we know that, b2 = a2(1 – e2)
⇒ b2 = a2 – a2e2
⇒ b2 = a2 – 9
or
a2 = b2 + 9 ….(iii)
On solving eq(ii), we get
16b2 + a2 = a2b2
Now put the value of a2 from eq(iii), we get
16b2 + b2 + 9 = (b2 + 9)b2
b4 – 8b2 – 9 = 0
⇒ b = ±3
So, a = 3√2
Now put the value of a2 and b2 in eq(i), we get
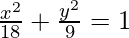
Thus, 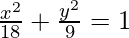 is the required equation.
is the required equation.
Question 12. Find the equation of an ellipse whose eccentricity is 2/3, the latus rectum is 5 and the centre is the origin.
Solution:
Let the equation of the ellipse be 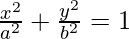 …..(i)
…..(i)
Given that
eccentricity(e) = 2/3
latus rectum = 5
So, 2b2/a = 5 …..(ii)
⇒ 2b2 = 5a
⇒ 10a2 = 45a
⇒ a = 9/2
On substituting the value of a in eq(ii), we have:
⇒ b2 = 45/4
Now put the value of a2 and b2 in eq(i), we get
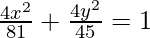
Thus, 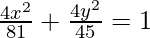 is the equation of the ellipse.
is the equation of the ellipse.
Question 13. Find the equation of the ellipse with its foci on the y-axis, eccentricity is 3/4, centre at the origin and passing through (6, 4).
Solution:
Let the equation of the plane be 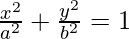
Given that
eccentricity(e) = 3/4,
As we know that a2 = b2(1 – e2)
⇒ 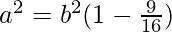
⇒ 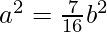
⇒ 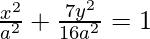
Since it passes through (6,4), we have:
⇒ 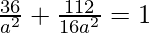
⇒ a2 = 43 and b2 = 688/7
Now put the value of a2 and b2 in eq(i), we get
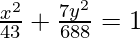
Thus 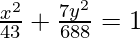 is the required equation.
is the required equation.
Question 14. Find the equation of the ellipse whose axes lie along coordinate axes and which passes through (4, 3) and (-1, 4).
Solution:
Let the equation of the ellipse be: 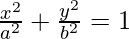 ….(i)
….(i)
It is given that the ellipse passes through (4, 3) and (-1, 4).
⇒ 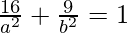 and
and 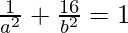
Let 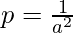 and
and 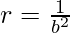
Then, 16p + 9r = 1 and p + 16b = 1
On solving these equations, we have:
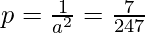 and
and 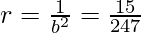
Now by substituting all the values in eq(i), we have:
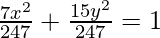
Thus, 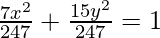 is the required equation.
is the required equation.
Question 15. Find the equation of an ellipse whose axes lie along the coordinate axes, which passes through the point(-3, 1) and has an eccentricity equal to 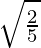 .
.
Solution:
Let the equation of the ellipse be: 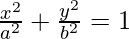 ……(i)
……(i)
It is given that the ellipse passes through the point (-3, 1).
So,
⇒ 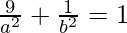
As we know that b2 = a2(1 – e2)
Also the eccentricity(e) = 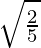 .
.
⇒ b2 = a2(1 – 2/5)
⇒ b2 = 3a2/5
On substituting the values, we have:
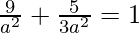
⇒ a2 = 32/2
⇒ b2 = 32/5
Now put the value of a2 and b2 in eq(i), we get
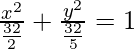
Thus, 3x2 + 5y2 = 32 is the required equation.
Question 16. Find the equation of the ellipse, the distance between the foci is 8 units, and the distance between directrices is 18 units.
Solution:
Let the equation of the ellipse be: 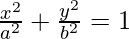 ……(i)
……(i)
Given that the distance between foci = 8 units
So, 2ae = 8 …(i)
Distance between directrices = 18 units
So, 2a/e = 18 …(i)
From eq(i) and (ii), we get
⇒ e = 8/2a
⇒ 4a2 = 18(8)
⇒ a2 = 36
⇒ a = 6
⇒ e = 2/3
Now, b2 = a2(1 – e2)
⇒ b2 = 36(1 – 4/9)
⇒ b2 = 36(5/9)
⇒ b2 = 20
Now put the values of a2 and b2 in eq(i), we get
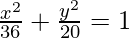
Thus, 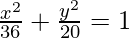 is the required equation.
is the required equation.
Question 17. Find the equation of the ellipse whose vertices are (0, ±10) and the eccentricity is 4/5.
Solution:
Let the equation of the ellipse be: 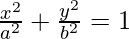 …..(i)
…..(i)
As we know that the vertices of the ellipse are on the y- axis, so the coordinates of the vertices are (0, ±10).
Thus, b = 10
Since, a2 = b2(1 – e2)
eccentricity(e) = 4/5 (given)
⇒ a2 = 100(1 – (4/5)2)
⇒ a2 = 100(1 – 16/25)
⇒ a2 = 36
Now put the values of a2 and b2 in eq(i), we get
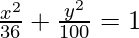
Thus, 100x2 + 36y2=3600 is the required equation.
Question 18. A rod of length 12m moves with its ends touching the coordinate axes. Determine the equation of the locus of a point P on the rod, which is 3 cm from the end in contact with x-axis.
Solution:
Let us consider AB be the rod that make an angle θ with line OX and let P(x, y) be the point on it such that AP = 3 cm.
Then, PB = AB – AP = 12 – 3 = 9 cm
Thus, 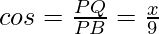
and, 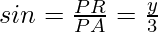
As we know that sin2θ + cos2θ = 1, we have:
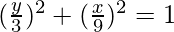
Thus 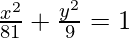 is the locus of the point P.
is the locus of the point P.
Question 19. Find the equation of the set of all points whose distances from (0, 4) are two-thirds of their distances from the line y = 9.
Solution:
Given that PQ = 2/3PL
So,
⇒ 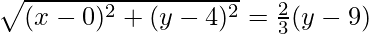
⇒ 32[x2 + (y – 4)2] = 22(y – 9)2
⇒ 9x2 + 9y2 – 72y + 144 = 4y2 – 72y + 324
⇒ 9x2 + 5y2 = 180
Thus 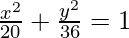 is the required equation.
is the required equation.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...