Euclid Euler Theorem
Last Updated :
16 Dec, 2022
According to Euclid Euler Theorem, a perfect number which is even, can be represented in the form  where n is a prime number and
where n is a prime number and 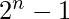 is a Mersenne prime number. It is a product of a power of 2 with a Mersenne prime number. This theorem establishes a connection between a Mersenne prime and an even perfect number.
is a Mersenne prime number. It is a product of a power of 2 with a Mersenne prime number. This theorem establishes a connection between a Mersenne prime and an even perfect number.
Some Examples (Perfect Numbers) which satisfy Euclid Euler Theorem are:
6, 28, 496, 8128, 33550336, 8589869056, 137438691328
Explanations:
1) 6 is an even perfect number.
So, it can be written in the form
(22 - 1) * (2(2 - 1)) = 6
where n = 2 is a prime number and 2^n - 1 = 3 is a Mersenne prime number.
2) 28 is an even perfect number.
So, it can be written in the form
(23 - 1) * (2(3 - 1)) = 28
where n = 3 is a prime number and 2^n - 1 = 7 is a Mersenne prime number.
3) 496 is an even perfect number.
So, it can be written in the form
(25 - 1) * (2(5 - 1)) = 496
where n = 5 is a prime number and 2^n - 1 = 31 is a Mersenne prime number.
Approach(Brute Force):
Take each prime number and form a Mersenne prime with it. Mersenne prime =  where n is prime. Now form the number (2^n – 1)*(2^(n – 1)) and check if it is even and perfect. If the condition satisfies then it follows Euclid Euler Theorem.
where n is prime. Now form the number (2^n – 1)*(2^(n – 1)) and check if it is even and perfect. If the condition satisfies then it follows Euclid Euler Theorem.
C++
#include <bits/stdc++.h>
using namespace std;
#define show(x) cout << #x << " = " << x << "\n";
bool isprime(long long n)
{
for (int i = 2; i * i <= n; i++)
if (n % i == 0)
return false;
return true;
}
bool isperfect(long long n)
{
long long s = -n;
for (long long i = 1; i * i <= n; i++) {
if (n % i == 0) {
long long factor1 = i, factor2 = n / i;
s += factor1 + factor2;
if (factor1 == factor2)
s -= i;
}
}
return (n == s);
}
int main()
{
vector<long long> power2(61);
for (int i = 0; i <= 60; i++)
power2[i] = 1LL << i;
cout << "Generating first few numbers "
"satisfying Euclid Euler's theorem\n";
for (long long i = 2; i <= 25; i++) {
long long no = (power2[i] - 1) * (power2[i - 1]);
if (isperfect(no) and (no % 2 == 0))
cout << "(2^" << i << " - 1) * (2^(" << i
<< " - 1)) = " << no << "\n";
}
return 0;
}
|
Java
class GFG
{
static boolean isprime(long n)
{
for (int i = 2; i * i <= n; i++)
{
if (n % i == 0)
{
return false;
}
}
return false;
}
static boolean isperfect(long n)
{
long s = -n;
for (long i = 1; i * i <= n; i++)
{
if (n % i == 0)
{
long factor1 = i, factor2 = n / i;
s += factor1 + factor2;
if (factor1 == factor2)
{
s -= i;
}
}
}
return (n == s);
}
public static void main(String[] args)
{
long power2[] = new long[61];
for (int i = 0; i <= 60; i++)
{
power2[i] = 1L << i;
}
System.out.print("Generating first few numbers " +
"satisfying Euclid Euler's theorem\n");
for (int i = 2; i <= 25; i++)
{
long no = (power2[i] - 1) * (power2[i - 1]);
if (isperfect(no) && (no % 2 == 0))
{
System.out.print("(2^" + i + " - 1) * (2^(" +
i + " - 1)) = " + no + "\n");
}
}
}
}
|
Python3
def isprime(n):
i = 2
while(i * i <= n):
if (n % i == 0):
return False;
i += 1
return False;
def isperfect(n):
s = -n;
i =1
while(i * i <= n):
if (n % i == 0):
factor1 = i
factor2 = n // i;
s += factor1 + factor2;
if (factor1 == factor2):
s -= i;
i += 1
return (n == s);
if __name__=='__main__':
power2 = [1<<i for i in range(61)]
print("Generating first few numbers satisfying Euclid Euler's theorem");
for i in range(2, 26):
no = (power2[i] - 1) * (power2[i - 1]);
if (isperfect(no) and (no % 2 == 0)):
print("(2^{} - 1) * (2^({} - 1)) = {}".format(i, i, no))
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static Boolean isprime(long n)
{
for (int i = 2; i * i <= n; i++)
{
if (n % i == 0)
{
return false;
}
}
return false;
}
static Boolean isperfect(long n)
{
long s = -n;
for (long i = 1; i * i <= n; i++)
{
if (n % i == 0)
{
long factor1 = i, factor2 = n / i;
s += factor1 + factor2;
if (factor1 == factor2)
{
s -= i;
}
}
}
return (n == s);
}
public static void Main(String[] args)
{
long []power2 = new long[61];
for (int i = 0; i <= 60; i++)
{
power2[i] = 1L << i;
}
Console.Write("Generating first few numbers " +
"satisfying Euclid Euler's theorem\n");
for (int i = 2; i <= 25; i++)
{
long no = (power2[i] - 1) * (power2[i - 1]);
if (isperfect(no) && (no % 2 == 0))
{
Console.Write("(2^" + i + " - 1) * (2^(" +
i + " - 1)) = " + no + "\n");
}
}
}
}
|
PHP
<?php
function isprime($n)
{
for ($i = 2; $i * $i <= $n; $i++)
if ($n % $i == 0)
return false;
return false;
}
function isperfect($n)
{
$s = -$n;
for ($i = 1;
$i * $i <= $n; $i++)
{
if ($n % $i == 0)
{
$factor1 = $i;
$factor2 = $n / $i;
$s += $factor1 + $factor2;
if ($factor1 == $factor2)
$s -= $i;
}
}
return ($n == $s);
}
$power2 = array();
for ($i = 0; $i <= 60; $i++)
$power2[$i] = 1<< $i;
echo "Generating first few numbers " .
"satisfying Euclid Euler's theorem\n";
for ($i = 2; $i <= 25; $i++)
{
$no = ($power2[$i] - 1) *
($power2[$i - 1]);
if (isperfect($no) &&
($no % 2 == 0))
echo "(2^" . $i . " - 1) * (2^(" .
$i . " - 1)) = " .
$no . "\n";
}
?>
|
Javascript
<script>
function isprime(n)
{
for (let i = 2; i * i <= n; i++)
{
if (n % i == 0)
{
return false;
}
}
return false;
}
function isperfect(n)
{
let s = -n;
for (let i = 1; i * i <= n; i++)
{
if (n % i == 0)
{
let factor1 = i, factor2 = n / i;
s += factor1 + factor2;
if (factor1 == factor2)
{
s -= i;
}
}
}
return (n == s);
}
let power2 = [];
for (let i = 0; i <= 60; i++)
{
power2[i] = 1 << i;
}
document.write("Generating first few numbers " +
"satisfying Euclid Euler's theorem" + "<br/>");
for (let i = 2; i <= 25; i++)
{
let no = (power2[i] - 1) * (power2[i - 1]);
if (isperfect(no) && (no % 2 == 0))
{
document.write("(2^" + i + " - 1) * (2^(" +
i + " - 1)) = " + no + "<br/>");
}
}
</script>
|
Output: Generating first few numbers satisfying Euclid Euler's theorem
(2^2 - 1) * (2^(2 - 1)) = 6
(2^3 - 1) * (2^(3 - 1)) = 28
(2^5 - 1) * (2^(5 - 1)) = 496
(2^7 - 1) * (2^(7 - 1)) = 8128
(2^13 - 1) * (2^(13 - 1)) = 33550336
(2^17 - 1) * (2^(17 - 1)) = 8589869056
(2^19 - 1) * (2^(19 - 1)) = 137438691328
Time Complexity: O(sqrt(n))
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...