Electrical potential energy is the cumulative effect of the position and configuration of a charged object and its neighboring charges. The electric potential energy of a charged object governs its motion in the local electric field. Sometimes electrical potential energy is confused with electric potential, however, the electric potential at a specific point in an electric field is the amount of work required to transport a unit charge from a reference point to that specific point and electrical potential energy is the amount of energy required to move a charge against the electric field.
In this article, let’s understand the electrical potential energy, electric potential, their key concepts, applications, and solved problems.
What is Electric Potential Energy?
The electric potential energy of a system of charges or a single charge is the total work done by an external force to bring the charge or system of charges from infinity to a reference point in an electric field without any acceleration.
Definition: Electric potential energy is the total energy possessed by a charge in order to change its position in the electric field.
Overview
As electrical potential energy has only magnitude and no direction, therefore it is a scalar quantity. The SI unit of electric potential energy is Joule (J). The following table shows some important points and symbols of the electric potential energy:
Electric Potential Energy
|
| Representation | UE or U |
| Dimensions | ML2T-2 |
| General Formula | UE = kq1q2/r |
| SI Unit | Joules |
Two factors are majorly responsible for the electric potential energy:
- The charge on the object.
- The relative position of the object with another neighboring charge.
Electric Potential Energy Formula
If W is the work done in transferring a unit positive charge q from infinity to a particular point in the electric field, this work done energy will be stored in form of the electric potential energy or electrostatic potential energy. Let’s derive the expression for electric potential energy,
Consider the electrostatic field E that exists as a result of a charge arrangement. Consider the electric field E caused by a charge Q placed at the origin for simplicity. Consider moving a test charge q from a point R to a point P while resisting the charge Q’s repulsive force. If Q and q are both positive or both negative, this will happen with reference. Let’s use Q as an example, with q > 0,

A test charge q (> 0) is moved from point R to point P against the repulsive force on it by the charge Q (> 0) placed at the origin.
Assume that the test charge q is so little that it has no effect on the original configuration, specifically the charge Q at the origin (or that Q is held fixed at the origin by some unknown force). Second, apply an external force Fext exactly enough to counter the repulsive electric force FE (i.e. Fext= –FE ) as the charge q move from R to P. This means that when the charge q is transported from R to P, it experiences no net force or acceleration, implying that it is transported at an infinitesimally slow constant speed. In this case, the work done by the external force is minus the work done by the electric force, and the potential energy of the charge q is fully stored. If the external force is withdrawn when the charge reaches P, the electric force will pull the charge away from Q – the stored energy (potential energy) at P is used to provide kinetic energy to the charge q, preserving the sum of the kinetic and potential energies.
Therefore, the work done by external forces in moving a charge q from R to P can be written as,
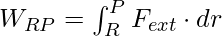
Since, Fext= –FE, then we can write,
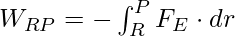
The above expression is the work done against electrostatic opposing force and gets stored as potential energy. A particle with charge q has a definite electrostatic potential energy at every location in the electric field. The work done raises its potential energy by an amount equal to the potential energy difference between points R and P. Therefore, the potential energy difference can be expressed as,
∆U = UP – UR = WRP
Note that this displacement is in the inverse direction of the electric force, hence the work done by the electric field is negative, i.e., –WRP.
As a result, the work required by an external force to move (without accelerating) charge q from one location to another for an electric field of any arbitrary charge configuration can be defined as the electric potential energy difference between two points. At this point, two key points should be made,
- The work done by an electrostatic field in transferring a charge from one location to another is solely reliant on the initial and final points and is unaffected by the path used to get there. This is a conservative force’s defining attribute.
- The above expression defines the difference in potential energy in terms of a physically meaningful quantity of work. Within an additive constant, potential energy is clearly uncertain. This indicates that the actual value of potential energy has no physical significance; only the change in potential energy is essential. We can always add an arbitrary constant to potential energy at any time since the potential energy difference will not change,
(UP – β ) – (UR – β ) = UP – UR
To put it another way, the point where potential energy is zero can be chosen at will. Electrostatic potential energy 0 at infinity is a convenient choice. If we take the point R at infinity with this option,
W∞P = UP – U∞ = UP – 0 = UP
The above expression defines the potential energy of a charge q at any moment in time.
The work done by the external force (equal and opposite to the electric force) in bringing the charge q from infinity to that location (in the presence of field due to any charge configuration) is called potential energy of charge q at a point.
Electric Potential Energy of a Point Charge
Consider the origin of a point charge Q. Consider Q to be a positive character. We wish to find the electrical potential energy at any location P using the position vector r from the origin. To do so, we need to figure out how much work it takes to transfer a unit-positive test charge from infinity to point P. When Q > 0, the work done against the repulsive force on the test charge is positive. Because the work is independent of the path, we choose a convenient path, i.e., along the radial direction from infinity to point P.

Work done in bringing a unit positive test charge from infinity to the point P, against the repulsive force of charge Q (Q > 0), is the potential at P due to the charge Q.
The electrostatic force on a unit positive charge at some intermediate point P′ on the path equals to
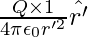
where  is the unit vector along OP’, therefore, work done against this force from r′ to r′ + ∆r′ can be written as
is the unit vector along OP’, therefore, work done against this force from r′ to r′ + ∆r′ can be written as
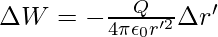
The negative sign represents ∆r′ < 0, and ∆W is positive. Total work done (W) by the external force is determined by integrating the above equation on both sides, from r′ = ∞ to r′ = r,
![Rendered by QuickLaTeX.com W=-\int_{∞}^{r} \frac{Q}{4\pi\epsilon_0r'^2}d{r'}\\ W=\left[\frac{Q}{4\pi\epsilon_0r'}\right]_∞^r\\ W=\frac{Q}{4\pi\epsilon_0r}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d2e0180c3df582bd6cbe1919ff24155a_l3.png)
The potential at P due to the charge Q can be expressed as,
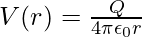
Electric Potential Energy of a System of Charges

Potential at a point due to a system of charges is the sum of potentials due to individual charges.
Suppose a system of charges q1, q2,…, qn with position vectors r1, r2,…, rn relative to some origin. The potential V1 at P due to the charge q1 can be expressed as
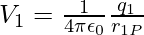
Where r1P is the distance between q1 and P.
Similarly, the potential V2 at P due to q2 and V3 due to q3 can be written as,
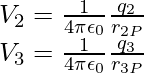
where r2P and r3P are the distances of P from charges q2 and q3, respectively, and so on for the potential due to other charges.
By the superposition principle, the potential V at P due to the total charge configuration is the algebraic sum of the potentials due to the individual charge, that is,
V = V1 + V2 + V3 +…. + Vn
The above expression can be expressed as,
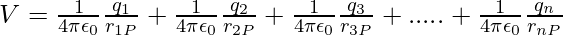
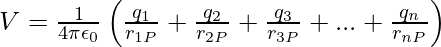
It is necessary to divide a continuous charge distribution with a charge density (r) into small volume elements of size ∆v, each carrying a charge ρ∆v. Then, for each volume element, compute the potential and add (or, more properly, integrate) all of these contributions to get the overall potential owing to the distribution.
What is Electric Potential?
The electric potential is defined as the amount of energy required to bring a unit mass object from a reference point to a specific point. If W amount of work is done to move an object of charge q from a point A to a reference point B. The formula for the electric potential can be expressed as,
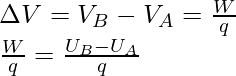
where VB and VA are the electric potentials at points B and A, respectively.
In general, think about any static charge configuration. A test charge’s potential energy q is defined in terms of the work done on it. This work is obviously proportional to q because the force at any position is qE, where E is the electric field at that site due to the given charge arrangement. As a result, dividing the work by the charge q yields a quantity independent of q.
The work done by an external force to carry a unit positive charge from infinity to a specific location is equal to the electrostatic potential (V) at that point.
In other words, the electrostatic potential (V ) at any place in an area with an electrostatic field is the work needed to transport a unit positive charge from infinity to that specific location (without acceleration). Electric potential is a scalar quantity with no direction and only magnitude. It is symbolized by V and has the dimensional formula ML2T-3A-1.

Work done on a test charge q by the electrostatic field due to any given charge configuration is independent of the path and depends only on its initial and final positions
The same caveats that were expressed before about potential energy apply to the definition of potential. To calculate the work done per unit test charge, start with an infinitesimal test charge δq, calculate the work done δW in bringing it from infinity to the point, and divide by δq to get the δW/δq ratio. In addition, at each point along the path, the external force must be equal to and opposite to the electrostatic force acting on the test charge.
What is Electric Potential Difference?
Electric potential difference is also known as voltage. The electric potential difference is the work done per unit charge to move a unit charge from one point to another in an electric field. Electric potential difference is usually referred to as a Voltage difference. Imagine a ball sitting at some height, will there be some energy in the ball? Yes, the energy is called Potential energy, and if the ball is dropped from a point A to B height, the ball will always fall from higher gravitational potential to lower, then there will be a difference in both energies. The electrical potential difference is analogical to this concept. The energy possessed by Electric charges is known as electrical energy. A charge with higher potential will have more potential energy, and a charge with lesser potential will have less potential energy. The current always moves from higher potential to lower potential. The formula for electric potential difference:
Vxy = Vx – Vy = [Wx – Wy]/q
Solved Examples on Electric Potential Energy
Example 1: Suppose you have a 12.0 V motorcycle battery that can move 5000 C of charge and a 12.0 V car battery that can move 60,000 C of charge. How much energy does each deliver?
Solution:
Given,
The voltage of the battery is V =12.0 V.
The charge that the motorcycle battery move is Q = 5000 C.
The 12.0 V car battery can move 60,000 C of charge.
When such a battery moves charge, it puts the charge through a potential difference of 12.0 V, and the charge is given a change in potential energy equal to Δ(PE) = qΔV.
For the motorcycle battery, q = 5000 C and ΔV = 12.0 V. The total energy delivered by the motorcycle battery is
ΔPEmotorcycle = (5000 C) × (12.0 V)
ΔPEmotorcycle = 6.00 × 104 J
Now, for the car battery,
ΔPEcar = (60,000 C) × (12.0 V)
ΔPEcar =7.20 × 105 J
Example 2: A particle of mass 40 mg carrying a charge 5 × 10-9 C is moving directly towards a fixed positive point charge of magnitude 10-8 C. When it is at a distance of 10 cm from the fixed point charge, it has a velocity of 50 cm/s. At what distance from the fixed point charge will the particle come momentarily to rest? Is the acceleration constant during motion?
Solution:
Given,
The mass of the particle m = 40 mg.
The charge of the particle Q = 5×10-9 C.
The fixed positive point charge of magnitude q =10-8 C.
Velocity of the charged particle is v = 50 cm/s = 0.5 m/s
The particle comes to rest momentarily at a distance r from the fixed charge, from conservation of energy we have,
According to the law of conservation of energy, the total energy of the system = Constant
i.e., (K.E. + P.E.) = constant.
The expression for the kinetic energy can be expressed as,
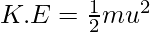
The expression for the potential energy can be expressed as,
Now,
(1/2)mu2 + (1/4πεo) × [Qq/a] = (1/4πεo) × [Qq/r]
(1/2)mu2 = (1/4πεo) [Qq/r – Qq/a]
(1/2)mu2 = (1/4πεo) Qq[1/r – 1/a]
Substituting the values in the above equation,
1/2 × 40 × 10-6 × (0.5)2= 9 × 109 × 10-8 × 5 × 10-9 × [ 1/r – 1/(10 × 10-2)]
or, [1/r – 10] = (5×10-5)/(9×5×10-8) = 100/9
or, 1/r = (100/9) + 10
or, 1/r = 190/9 m
or r = 4.7 × 10-2 m
Since, F = [1/4πεo] × [Qq/r2]
Therefore, acceleration = F/m ∝ 1/r2 , i.e., acceleration is not constant during motion.
Example 3: A ball of mass 5 g and charge 10-7 C moves from point A, whose potential is 500 V, to point B, whose potential is zero. What is the velocity of the ball at point A if at point B, it is 25 cm per second?
Solution:
Given,
The mass ball is 5 g.
The charge of the particle is 10-7 C.
The potential of ball at point A is 500 V and potential at point B is zero.
Suppose u be the velocity of the ball at point A.
The work done on the charge by the field given by,
W = q × (VA – VB)
Substitute the value in the above expression,
W = 10-7 C× (500 V – 0 V)
W = 5 × 10-5 J
Therefore,
W = (1/2) mv2 – (1/2) mu2
5 × 10-5 J= (1/2) × (5/1000 )×[(1/4)2 – u2]
2 × 10-2 = 1/16 – u2
u2 = (1/16) – 0.02
u2 = (1- 0.32)/16
u2 = 0.0425
Therefore, u =0.206 m/s
u = 20.6 cm/s.
Example 4: When a 12.0 V car battery runs a single 30.0 W headlight, how many electrons pass through it each second?
Solution:
The expression for the potential energy can be written as,
Δ(PE) = qΔV
Rearrange the above expression,
q = Δ(PE)/ΔV
Substitute the values in the above equation,
q = −30.0 J/ 12.0 V
q = −30.0 J/ 12.0 J/C
q = −2.50 C
The number of electrons n can be calculated as,
n = q/e
n = −2.50 C/(−1.60 × 10−19 C/e)
n = 1.56 × 1019 electrons
Example 5: How much work is required to be done in order to bring two charges of magnitude 3 C and 5 C from a separation of infinite distance to a separation of 0.5 m?
Solution:
Given,
Two charges of magnitude 3 C and 5 C.
The separation between two charges are 0.5 m.
The potential at P due to the charge Q can be expressed as
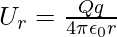
∆U = U0 – Ur
∆U = 0 J – [-(9 × 109 Nm2/C2× 5 C × 3 C)/0.5 m] J = 2.7 × 1011J.
Therefore, ∆U = 2.7 × 1011 J.
FAQs on Electric Potential Energy
Question 1: What is electric potential energy?
Answer:
Electric potential energy of a single charge or system of charges is the energy required by an external force in moving a charge in the electric field.
Question 2: List some examples of electric potential energy.
Answer:
Some examples of electric potential energy are:
- Air-conditioner system before turning on.
- Vacuum cleaner after turning off.
- Television before turning on.
- Car’s headlights before it is turned on.
Question 3: What is the electrical potential energy formula?
Answer:
The formula for electrical potential energy is:
UE = k (q1q2)/r
Where,
- UE = Electric potential energy
- k = Coulomb constant
- q1, q2 = Charges
- r = Distance between charges
Share your thoughts in the comments
Please Login to comment...