When an external force is used to remove a body from a situation. Point to another in the face of a force like spring or gravitational force That work is stored in the body as potential energy. When the external environment When a force is eliminated, the body moves, gaining and losing kinetic energy. An amount of potential energy that is equal. The total amount of kinetic and As a result, potential energy is conserved. This type of force is referred to as Conservative forces are at work. Examples of forces include spring force and gravitational force. Conservative forces are at work.
What are Conductors?
A metal rod rubbed with wool in the hand will not exhibit any evidence of being charged. A metal rod with a wooden or plastic grip, on the other hand, exhibits symptoms of charge when brushed with wool without touching its metal part. Consider a copper wire with one end linked to a neutral pith ball and the other to a negatively charged plastic rod. The pith ball acquires a negative charge, as can be seen. A similar experiment using a nylon thread or a rubber band yielded no charge transfer from the plastic rod to the pith ball.
Conductors are materials that permit the free flow of electricity through them. Inside the material, they have comparatively free-moving electric charges (electrons). Metals, human and animal bodies, and the ground itself are all conductors.
As a safety measure, earthing electrical circuits and equipment are beneficial. A large metal plate is buried deep in the ground, and thick wires are dragged from it to connect houses to the earth near the mains supply. The electrical wiring in our homes is made up of three wires: live, neutral, and earth. The first two transport power from the power plant, while the third is earthed by connecting to a buried metal plate. Electric equipment such as electric irons, refrigerators, and televisions have an earth wire that is attached to the metallic body. When a fault happens or a live wire comes into contact with the metallic body, the charge flows to the earth without destroying the appliance or injuring humans; otherwise, because the human body is a conductor of electricity, this would have been unavoidable.
Electrostatics of Conductors
Mobile charge carriers are found in conductors. Electrons are the charge carriers in metallic conductors. The outside (valence) electrons of metal separate from their atoms and become free to move. These electrons are free to move about within the metal but not outside it. The liberated electrons form a kind of ‘gas,’ colliding with one other and the ions as they move in random directions. They float in the opposite direction of an external electric field. The positive ions, which are made up of nuclei and bound electrons, are maintained in place. The charge carriers in electrolytic conductors are both positive and negative ions; however, the situation is more complicated in this case since the charge carriers’ movement is influenced by both the external electric field and the so-called chemical forces. Let’s take a look at some key findings in conductor electrostatics.
- Inside a conductor, an electrostatic field is zero.
Consider a neutral or charged conductor. There could also be an electrostatic field outside the room. The electric field is zero everywhere inside the conductor in a static scenario, when there is no current inside or on the surface of the conductor. This fact can be considered a conductor’s defining characteristic. Free electrons exist in a conductor. The free charge carriers will suffer force and drift as long as the electric field is not zero. The free charges have dispersed themselves so evenly inside the static condition that the electric field is zero everywhere. Inside a conductor, the electrostatic field is zero.
- At the surface of a charged conductor, the electrostatic field must be normal to the surface at every point.
E would have a non-zero component along the surface if it wasn’t normal to the surface. The free charges on the conductor’s surface would then be forced to shift. As a result, in a static scenario, E should have no tangential component. As a result, the electrostatic field at the surface of a charged conductor must be perpendicular to the surface at all times. (Field is zero even at the surface of a conductor with no surface charge density.)
- The interior of a conductor can have no excess charge in a static situation.
Every little volume or surface element in a neutral conductor has the same quantity of positive and negative charges. When the conductor is charged in a static condition, the excess charge can only dwell on the surface. This is based on Gauss’s law. Consider a conductor with any arbitrary volume element v. The electrostatic field is zero on the closed surface S that surrounds the volume element v. As a result, the total electric flux passing through S is zero. As a result, according to Gauss’ law, there is no net charge enclosed by S. However, the surface S can be made as small as desired, resulting in a vanishingly small volume v. This means that there is no net charge inside the conductor at any point, and any excess charge must be discharged at the surface.
- The electrostatic potential is constant throughout the volume of the conductor and has the same value (as inside) on its surface.
This follows the point 1 and 2 which is mention above. There is no work done in moving a small test charge within the conductor and on its surface because E = 0 inside the conductor and has no tangential component on the surface. That is, no potential difference exists between any two places inside or on the conductor’s surface. As a result, the outcome. If the conductor is charged, an electric field normal to the surface exists; this means the surface and a point just outside the surface have different potentials. Each conductor in a system of conductors of arbitrary size, shape, and charge arrangement is defined by a constant value of potential, which may differ from one conductor to the next.
- The electric field at the surface of a charged conductor
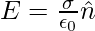 …………….(1)
…………….(1)
where σ is the surface charge density and 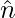 is a unit vector normal to the surface in the outward direction.
is a unit vector normal to the surface in the outward direction.

The Gaussian surface (a pillbox) was chosen to derive the electric field at the surface of a charged conductor.
To get the result, choose a pillbox (a short cylinder) as the Gaussian surface around any point P on the surface, as shown in the above figure. The pillbox is partially inside and partially outside the conductor’s surface. It has a tiny cross-sectional area δS and a low height. The electrostatic field is zero just inside the surface, and it is normal to the surface with magnitude E just outside. As a result, only the pillbox’s outside (circular) cross-section contributes to the total flux through the pillbox. This equals ES (positive for σ > 0, negative for σ < 0), because E is constant over the tiny area S, and E and S are parallel or antiparallel. σ δS is the charge carried by the pillbox.
According to Gauss’s law,
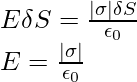
The fact that the electric field is perpendicular to the surface, the vector relation, equation (1) is true for both signs of σ. For σ > 0, the electric field is normal to the surface outward; for σ < 0, the electric field is normal to the surface inward.
Consider a conductor with a hollow that contains no charges. The electric field inside the cavity is zero, regardless of the size and shape of the cavity and the charge on the conductor, and the external fields in which it may be positioned. This result has already been shown in a basic case: the electric field inside a charged spherical shell is zero. The spherical symmetry of the shell is used in the proof of the result for the shell. However, as previously stated, the disappearance of the electric field in the (charge-free) cavity of a conductor is a very general result. A related result is that all charges remain only on the outer surface of a conductor with a cavity, even if the conductor is charged or charges are induced on a neutral conductor by an external field.

8The electric field inside the cavity of any conductor is zero. All charges reside only on the outer surface of a conductor with a cavity. (There are no charges placed in the cavity.)
The proofs of the above-mentioned results are omitted in the above figure, but their significance is highlighted. Any cavity in a conductor is protected from outside electric effect, regardless of the charge and field configuration outside: the field inside the cavity is always zero.

Some important electrostatic properties of a conductor
Electrostatic shielding is the term for this. The effect can be used to shield delicate devices from electrical interference from the outside world. The electrostatic properties of a conductor are summarized in the above figure.
Sample Problems
Problem 1: (a) A comb run through one’s dry hair attracts small bits of paper. Why? What happens if the hair is wet or if it is a rainy day? (Remember, the paper does not conduct electricity.)
(b) Ordinary rubber is an insulator. But special rubber tyres of aircraft are made slightly conducting. Why is this necessary?
(c) Vehicles carrying inflammable materials usually have metallic ropes touching the ground during motion. Why?
(d) A bird perches on a bare high power line, and nothing happens to the bird. A man standing on the ground touches the same line and gets a fatal shock. Why?
Solution:
(a) This is because the comb gets charged by friction. The molecules in the paper gets polarised by the charged comb, resulting in a net force of attraction. If the hair is wet, or if it is a rainy day, friction between hair and the comb reduces. The comb does not get charged, and thus it will not attract small bits of paper.
(b) To enable them to conduct charge (produced by friction) to the ground; as too much of static electricity accumulated may result in spark and result in fire.
(c) To enable them to conduct charge (produced by friction) to the ground; as too much of static electricity accumulated may result in spark and result in fire.
(d) Current passes only when there is a difference in potential.
Problem 2: A slab of material of dielectric constant K has the same area as the plates of a parallel-plate capacitor but has a thickness (3/4)d, where d is the separation of the plates. How is the capacitance changed when the slab is inserted between the plates?
Solution:
Let E0 = V0 /d be the electric field between the plates when there is no dielectric and the potential difference is V0 . If the dielectric is now inserted, the electric field in the dielectric will be E = E0 /K. The potential difference will then be
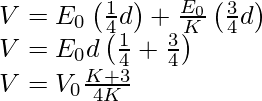
The potential difference decreases by the factor (K + 3)/K while the free charge Q0 on the plates remains unchanged. The capacitance thus increases
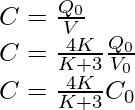
Problem 3: A 500 µC charge is at the Centre of a square of side 10 cm. Find the work done in moving a charge of 10 µC between two diagonally opposite points on the square.
Solution:
The work done in moving a charge of 10 µC between two diagonally opposite points on the square will be zero because these two points will be at equipotential.
Problem 4: Why must the electrostatic potential inside a hollow charged conductor be the same at every point?
Solution:
Because the electric field inside the hollow charged conductor is zero, no work is done in moving a small test charge within the conductor. As a result, the electrostatic potential inside a hollow charged conductor remains constant.
Problem 5:
(i) Can two equipotential surfaces intersect each other? Give reasons.
(ii) Two charges -q and + q are located at points A (0, 0, – a) and B (0, 0, +a) respectively. How much work is done in moving a test charge from point P (7, 0, 0) to Q (-3,0,0)?
Solution:
(i) No, if they intersect, the electric field will be in two distinct directions, which is incorrect. If they cross, there will be two potential values at the same place of intersection. Because this isn’t conceivable, two equipotential surfaces can’t meet.
(ii) Work done will be zero since both points P and Q are on the dipole’s equatorial line, which has V = 0 at all points. Furthermore, because any charge’s force is perpendicular to the equatorial line, no work is done.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...