Electric Potential Due to System of Charges
Last Updated :
05 Sep, 2023
Electric Potential is defined as the force experienced by a charge inside the electric field of any other charge. mathematically it is defined as the ratio of electric potential energy that is required to take a test charge from infinity to a point inside the electric field of any other charge with the magnitude of the test charge.
Electric potential at any point is determined by the number and orientation of the test charges arranged in their surroundings and their distance from those charges. In this article we will learn about electric potential due to system of charges, its formula, examples and other in detail.
What is Electric Potential?
Electric potential is defined as the difference in the potential energy per unit charge between two places. To check the difference in the electric potential between two positions under the influence of an electric field, we ask ourselves how much the potential energy of a unit positive charge will change if that charge is moved from this position to the other position. It is denoted by V,
V = P.E/q
Electric Potential Due to Point Charge
A point charge is given in the figure below. The concentric circles represent the equipotential. That means, that at all the points in a single surface, the potential is the same. The goal is to calculate the electric potential due to this point charge between two points A and B.

Electric potential difference is also called voltage, and it is measured in the units of Volts.
VoltageAB = Electric potential differenceAB = 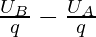
The potential has been defined as a difference; a formulation in terms of absolute potential is required. Let’s modify the above formulation to come up with this new definition. At infinite, the electric field and the potential are assumed to be zero. Now, the potential at every point will be calculated with respect to the infinite, and it will give an absolute value of the potential.
Now, rB = ∞ and rA
VoltageAB = 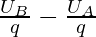
= 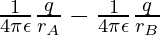
Now, rB = ∞
= 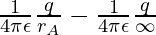
= 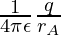
Electric Potential Due to System of Charges
A single-point charge is rarely encountered in real life. Most of the systems found in real-life comprise multiple charges. For a system of point charges, the total potential at a point is given by the algebraic sum of the potential for individual charges at that point. The figure given below represents a system of point charges.

For example, in a system containing charges q1, q2, q3 at a distance of r1P, r2P, and r3P from a point. Then, the potential at this point by individual charges will be given by,
V1 = 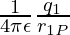 ,
,
V2 = 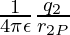 ,
,
V3 = 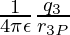
The net potential due to these point charges is given by,
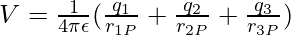
In general,
For a system of point charges containing charges q1, q2, q3,q4 …. at a distance of r1P, r2P and r3P…. from a point.
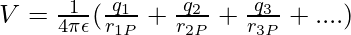
Solved Examples on Electric Potential
Example 1: Find the potential at a distance of 2 m from a point charge of 20pC.
Solution:
Potential due to a point charge is given by,
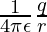
Here,
- q = 20 pC = 2 x 10-12 C
- r = 2 m
Plugging the values into this equation,
V = 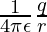
⇒ V = 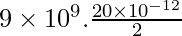
⇒ V = 9 × 109 × 1 × 10-11
⇒ V = 9 × 10-2 V
Example 2: Find the potential at a distance of 5m from a point charge of 10pC.
Solution:
Potential due to a point charge is given by,
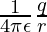
Here,
- q = 10 pC =10 × 10-12 C
- r = 5 m
Plugging the values into this equation,
V = 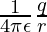
⇒ V = 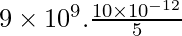
⇒ V= 9 × 109 × 2 × 10-12
⇒ V= 18 x 10-3 V
Example 3: Find the potential at a distance of 1 m due to a charge of 10pC and -2pC.
Solution:
Potential due to a point charge is given by,
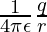
Here,
- q1 = 10 pC = 10 x 10-12 C
- q2 = -2 pC = -2 x 10-12 C
- r = 1 m
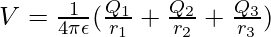
For two charges,
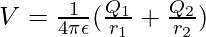
Plugging the values into this equation,
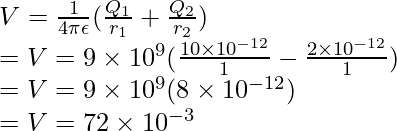
⇒ V= 36 × 10-3 V
Example 4: Find the potential at the center of a square of side a=2m due to a charge of 2pC and 2pC.

Solution:
Potential due to a point charge is given by,
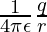
Here,
- q1 = 2 pC = 2 x 10-12 C
- q2 = 2 pC = -2 x 10-12 C
Since the square is of side a = 2. The length of the diagonal will be 2√2.
This distance of the point from both the charges will be √2.
Thus,
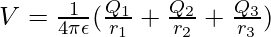
For two charges,
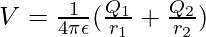
Plugging the values into this equation,
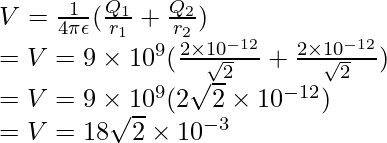
Example 5: Find the potential at the origin due to the charges 1pC and -1pC located at (0,1) and (2,0).
Solution:
Potential due to a point charge is given by,
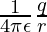
Here,
- q1 = 1 pC = 1 x 10-12 C
- q2 = 2 pC = -1 x 10-12 C
Distance of these charges from the center is,
Since there are two charges in the system, the total potential will be given by the superposition equation.
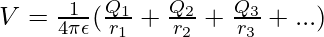
For two charges,
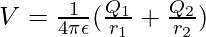
Plugging the values into this equation,
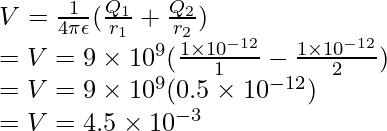
Example 6: Find the potential at the origin due to the charges 2pC and -10pC located at (0,3,4) and (0,0,5).
Solution:
Potential due to a point charge is given by,
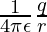
Here,
- q1 = 1 pC = 1 x 10-12 C
- q2 = 2 pC = -1 x 10-12 C
Distance of these charges from the center is,
- r1 = √(02 + 32 + 42) = √(25) = 5
- r2 = 5
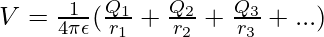
For two charges,
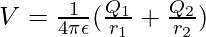
Plugging the values into this equation,
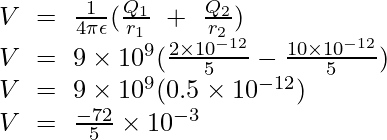
Electric Potential-FAQs
1. What is an Electric Charge?
Electric Charge is the property of the material that is used to define the electrostatic and electromagnetic properties of the material. There are two types of charges Positive Chagre and Negative Charge.
2. What is Electric Potential?
Electric potential is defined as the electric potential energy of a test charge placed at a point, divided by the magnitude of the charge. It is denoted by “V” and its formula is,
V = U / q
where,
- U is the Electric Potential Energy
- q is the charge
3. What is the SI unit of Electric Charge?
The SI unit of Electric Charge is “Columb” or “C”.
4. What is the SI unit of Electric Potential?
The SI unit of Electric Potential is “Volt” or “V”.
5. What is an Electric Dipole?
We define electric dipole by the two a set up that is formed by two charges separated by a distance “2d”. Then the electric dipole is the product of the charge and distance between them. It is denoted by “P”.
P = q.d
where,
- q is the charge
- d is the distance between them
Share your thoughts in the comments
Please Login to comment...