Gauss law is defined as the total flux out of the closed surface is equal to the flux enclosed by the surface divided by the permittivity. The Gauss Law, which analyses electric charge, a surface, and the issue of electric flux, is analyzed. Let us learn more about the law and how it functions so that we may comprehend the equation of the law.
What is Gauss Law?
According to gauss law, the total electric flux out of a closed surface is equal to the charge contained divided by the permittivity. The electric flux in a given area is calculated by multiplying the electric field by the area of the surface projected in a plane perpendicular to the field. The total flux associated with a closed surface equals 1 ⁄ ε0 times the charge encompassed by the closed surface, according to the Gauss law.
∮ E.ds = q ⁄ εo
For example, a point charge ‘q’ is put within a cube with the edge ‘a’. The flux across each face of the cube is now q ⁄ 6εo, according to Gauss law. The electric field is the most fundamental concept in understanding electricity. In general, the electric field of a surface is computed using Coulomb’s law; however, understanding the idea of Gauss’ law is required to calculate the electric field distribution in a closed surface. It describes how an electric charge is enclosed in a closed surface or how an electric charge is present in a closed surface that is enclosed.
Gauss Law Formula
According to the Gauss law formula, the total electric charge enclosed in a closed surface is proportional to the total flux enclosed by the surface. As a consequence, the total electric charge Q contained by the surface is: if ε0 is electric constant and ϕ is total flux.
Q = ϕ εo
The formula of Gauss law is given by:
ϕ = Q⁄εo
Where,
- εo is electrostatic constant,
- Q is total charge within a given surface, and
- ϕ is flux enclosed by surface.
The Gauss Theorem
The Gauss theorem connects the ‘flow’ of electric field lines (flux) to the charges within the enclosed surface in simple terms. The net charge in the volume contained by a closed surface is exactly proportional to the net flux through the closed surface.
ϕ = E.dA = qnet ⁄ εo
The net electric flow stays 0 if no charges are contained by a surface. The number of electric field lines entering the surface equals the number of field lines exiting the surface.
A corollary of the gauss theorem statement:
The electric flux from any closed surface is only due to the sources and sinks of electric fields enclosed by the surface. The electric flux is unaffected by any charges outside the surface. Furthermore, only electric charges may operate as electric field sources or sinks. It is important to note that changing magnetic field cannot act as electric field sources or sinks.
As it encloses a net charge, the net flow for the surface on the left is non-zero. Because the right-hand surface does not contain any charge, the net flow is zero. The Gauss law is nothing more than a repetition of Coulomb’s law. Coulomb’s law is readily obtained by applying the Gauss theorem to a point charge surrounded by a sphere.
Note: Gauss’ law and Coulomb’s law are closely related. If gauss law is applied to a point charge in a sphere, it will be the same as applying coulomb’s law.
Gauss Law Equation
Gauss law equation can be understood using an integral equation. Gauss’s law in integral form is mentioned below:
∫E.dA = Q/ε0 ⇢ (1)
Where,
- E is the electric field
- Q is the electric charge enclosed
- ε0 is the electric permittivity of free space
- A is the outward pointing normal area vector
Flux is a measure of the strength of a field passing through a surface. Electric flux is given as:
Φ = ∫E⋅dA ⇢ (2)
Application of Gauss Law
There are different formulae obtained from the application of Gauss law for different conditions. Below are some well-known applications of Gauss law:
- In a medium with a dielectric constant of K, the strength of the electric field near a plane-charged conductor E = σ ⁄ K εo. Eair = σ ⁄ εo when the dielectric medium is air.
- At a distance of ‘r’ in the case of an infinite charge line, E = (1 ⁄ 4 × π r ε0) (2π ⁄ r) = λ ⁄ 2π r εo, where λ is linear charge density.
- In a condenser or capacitor, the field between two parallel plates is E = σ ⁄ ε0, where σ is the surface charge density.
- The electric field strength near a plane sheet of charge is E = σ ⁄ 2K εo, where σ is the surface charge density.
- For a charged ring having a radius ‘R’, from the centre of the ring at a distance ‘x’, here, the electric field becomes:
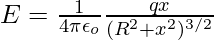
Gauss Law Derivation – Electric Field due to Infinite Wire
To find the electric field due to an infinite wire, assume the charge per unit on the infinitely long wire is λ. The electric field is radially away from all points of the wire, and no component is parallel to the line of charge. Now, assume the wire as a cylinder (with radius ‘r’ and length ‘l’) centered on the line of charge as the gaussian surface.
The electric field is perpendicular to the cylinder. Hence, the angle between the electric field and area vector is 0°. So, cosθ = 1. The top and bottom of the cylinder are parallel to the electric field. Hence, the area vector here is 90° w.r.t. the electric field. Therefore, cosθ = 0. Hence, we can say that the electric flux occurs only due to the curved surface of the cylinder. According to gauss law:
ϕ = E.d ⇢ A
ϕnet = ϕcurved + ϕtop + ϕbottom
ϕ = E.d ⇢ A = ∫E.dA cos0 + ∫E.dA cos90 + ∫E.dA cos90
ϕ = ∫E.dA
The curved surface is equidistant from the line of charge due to its radial symmetry. So, the electric field on the surface has a constant value throughout the surface.
ϕ = ∫E.dA = ∫E. 2πrl
The net charge enclosed by the surface:
qnet = λ.l
Now, using gauss theorem:
ϕ = ∫E. 2πrl = qnet ⁄ εo = λ.l/εo
∫E. 2πrl = λ.l/εo
E = λ/2πrεo
Solved Examples on Gauss Law
Example 1: In the x-direction, there is a homogeneous electric field of size E = 50 N⁄C. Calculate the flux of this field across a plane square area with an edge of 5 cm in the y-z plane using the Gauss theorem. Assume that the normal is positive along the positive x-axis.
Solution:
Given:
Electric field, E = 50 N⁄C
Edge length of square, a = 5 cm = 0.05 m
The flux of the field across a plane square, ϕ = ∫ E cosθ ds
As the normal to the area points along the electric field, θ = 0.
Also, E is uniform so, Φ = E ΔS = (50 N⁄C) (0.05 m)2 = 0.125 N m2 C-1.
Hence, the flux of the given field is 0.125 N m2 C-1.
Example 2: There are three charges, q1, q2, and q3, having charges 4 C, 7 C, and 2 C enclosed in a surface. Find the total flux enclosed by the surface.
Solution:
Total charge Q,
Q = q1 + q2 + q3
= 4 C + 7 C + 2 C
= 13 C
The total flux, ϕ = Q ⁄ ε0
ϕ = 13 C ⁄ (8.854×10−12 F ⁄ m)
ϕ = 1.468 N m2 C-1
Therefore, the total flux enclosed by the surface is 1.584 N m2 C-1.
Example 3: Two conducting plates having charges Q1 and Q2, are kept parallel to each other. Find the distribution on all four surfaces.
Solution:
It can be seen from the figure that two faces lie inside the conductor when E = 0. The flux is also 0. The faces that are outside are parallel to the electric field, the flux there will be 0 too. Therefore, the total flux of the electric field is 0.
From gauss law, the total charge inside the closed surface must be 0. Therefore, the charge on the inner side of one plate should be equal to the charge on the other side.
Using the equation E = σ/2ε0, the electric field at P:
- Due to the charge Q1 – q = (Q1 – q)/2Aε0 (downward).
- Due to the charge +q = +q/ε0 (upward).
- Due to the charge Q2 + q = (Q2 + q)/2Aε0 (upward)
- Due to the charge -q = -q/ε0 (downward).
The net electric field is in the downward direction:
(Q1 – q)/2Aε0 + (-q/ε0) + (Q2 + q)/2Aε0 + +q/ε0
Q1 -q +q -Q2 = 0
q = (Q1 – Q2)/2
Q1 – q = (Q1 + Q2)/2
Q2 + q = (Q1 + Q2)/2
Example 4: What is the differential form of the Gauss theorem?
Solution:
The electric field is related to the charge distribution at a certain location in space by the differential version of Gauss law. To clarify, according to the law, the electric field’s divergence (E) is equal to the volume charge density (ρ) at a given position. It’s written like this:
ΔE = ρ ⁄ ε0
Here, ε0 is the permittivity of free space.
Example 5: There are three concentric spherical shells A, B, and C with radii a, b, and c. The charges are present on shells A and C (q and -q respectively), and shell B is earthed. Find the total charges appearing on B and C.
Solution:
Since the inner surface of shell B must have a charge of -q, suppose the outer surface of B has a charge ‘x’. Then, the inner surface of C must have a charge of ‘-x’.
Potential due to charge ‘q’ on A = q/4πε0b
Potential due to ‘-q’ on inner surface of B = -q/4πε0b
Potential due to ‘x’ on outer surface of B = x/4πε0b
Potential due to ‘-x’ on inner surface of C = -x/4πε0c
Potential due to ‘x – q’ on inner surface of C = x – q/4πε0c
Now, the net potential: VB = x/4πε0b – q/4πε0c
This potential is equated to 0 as the shell B is earthed.
Therefore, x = qb/c
Below is the figure showing the charges on each surface:
FAQs on Gauss Law
Question 1: State Gauss law.
Answer:
Gauss law states that the net flux of an electric field is directly proportional to the charge enclosed in a closed surface.
Question 2: How do we choose an appropriate Gaussian Surface for different cases?
Solution:
In order to select an acceptable Gaussian Surface, we must consider the fact that the charge-to-dielectric constant ratio is supplied by a (two-dimensional) surface integral over the charge distribution’s electric field symmetry.
We’ll need to know about three potential scenarios.
- When the charge distribution is spherically symmetric, it is called spherical.
- When the charge distribution is cylindrically symmetric, it is called cylindrical.
- When the charge distribution exhibits translational symmetry along a plane, it is called a pillbox.
Depending on where we want to compute the field, we may determine the size of the surface. The Gauss theorem is useful for determining the direction of a field when there is symmetry, as it informs us how the field is directed.
Question 3: State gauss law in electrostatics.
Solution:
Gauss law in electrostatics states that the electric flux through any closed surface is equal to the net charge enclosed by the surface divided by the permittivity of free space.Normally, the Gauss law is employed to calculate the electric field of symmetric charge distributions. When using this law to solve the problem of the electric field, there are numerous processes required. The following are the details:
- First, we must determine the charge distribution’s spatial symmetry.
- The next step is to select a proper Gaussian surface that has the same symmetry as the charge distribution. Its ramifications must also be determined.
- Calculate the flux across the surface by evaluating the integral ϕs E over the Gaussian surface.
- Calculate the amount of charge contained within the Gaussian surface.
- Calculate the charge distribution’s electric field.
However, in order to determine the electric field, pupils must remember the three forms of symmetry. The following are the several forms of symmetry:
- Symmetry on a sphere
- Symmetry in a cylindrical shape
- Symmetry on a plane
Question 4: What are the applications of Gauss law?
Answer:
Complex electrostatic problems involving symmetry like cylindrical, spherical, etc. can be solved using Gauss law. It also helps solving for the electric field that involves complex calculations.
Question 5: What is Gaussian surface?
Answer:
Gaussian surface is the surface through which electric flux is calculated.
Question 6: State Gauss law for magnetism.
Answer:
Gauss law for magnetism states that the magnetic flux across any closed surface is 0. This can be written as Div. B = 0, where Div. B is the divergence factor of B.
Gauss’s Law is a fundamental principle in physics that relates the electric field to the distribution of electric charges. It states that the total electric flux through any closed surface is equal to the total charge enclosed by the surface divided by the permittivity of free space (ε0). Mathematically, Gauss’s Law can be expressed as:
∮S E · dA = Qenc/ε0
where ∮S represents the surface integral over a closed surface S, E is the electric field vector, dA is the surface area vector, Qenc is the total charge enclosed by the surface, and ε0 is the permittivity of free space.
Gauss’s Law is a powerful tool for calculating electric fields in situations where the symmetry of the charge distribution makes it difficult to use Coulomb’s Law. By using Gauss’s Law, it is possible to calculate the electric field of a uniformly charged sphere, cylinder, or plane, for example.
Gauss’s Law has important applications in many areas of physics, including electromagnetism, electrostatics, and quantum mechanics. It is used to analyze the behavior of electric fields in charged particles, capacitors, and other electrical devices. It also plays a key role in the understanding of electromagnetic radiation and the propagation of radio waves.
Related Articles
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...