Degree Centrality (Centrality Measure)
Last Updated :
21 Jul, 2022
Degree
In graph theory, the degree (or valency) of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice.[1] The degree of a vertex
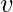
is denoted
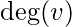
or
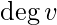
. The maximum degree of a graph G, denoted by

(G), and the minimum degree of a graph, denoted by
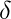
(G), are the maximum and minimum degree of its vertices. In the graph on the right, the maximum degree is 5 and the minimum degree is 0. In a regular graph, all degrees are the same, and so we can speak of the degree of the graph.
Degree Centrality
Historically first and conceptually simplest is degree centrality, which is defined as the number of links incident upon a node (i.e., the number of ties that a node has). The degree can be interpreted in terms of the immediate risk of a node for catching whatever is flowing through the network (such as a virus, or some information). In the case of a directed network (where ties have direction), we usually define two separate measures of degree centrality, namely indegree and outdegree. Accordingly, indegree is a count of the number of ties directed to the node and outdegree is the number of ties that the node directs to others. When ties are associated to some positive aspects such as friendship or collaboration, indegree is often interpreted as a form of popularity, and outdegree as gregariousness.
The degree centrality of a vertex
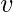
, for a given graph
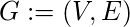
with
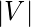
vertices and
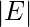
edges, is defined as
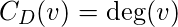
Calculating degree centrality for all the nodes in a graph takes
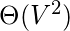
in a dense adjacency matrix representation of the graph, and for edges takes
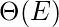
in a sparse matrix representation.
The definition of centrality on the node level can be extended to the whole graph, in which case we are speaking of graph centralization. Let
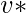
be the node with highest degree centrality in
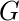
. Let
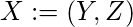
be the
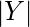
node connected graph that maximizes the following quantity (with
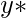
being the node with highest degree centrality in
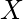
):
![Rendered by QuickLaTeX.com H=\sum _{{j=1}}^{{|Y|}}[C_{D}(y*)-C_{D}(y_{j})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d616b7765f6a06a2b7a0e0329204f1e5_l3.png)
Correspondingly, the degree centralization of the graph
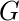
is as follows:
![Rendered by QuickLaTeX.com C_D(G)= \frac{\displaystyle{\sum^{|V|}_{i=1}{[C_D(v*)-C_D(v_i)]}}}{H}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8fd1efa8a22b052357833503d2ab120f_l3.png)
The value of
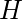
is maximized when the graph
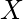
contains one central node to which all other nodes are connected (a star graph), and in this case
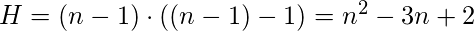
.
Following is the code for the calculation of the degree centrality of the graph and its various nodes.
import networkx as nx
def degree_centrality(G, nodes):
r
top = set(nodes)
bottom = set(G) - top
s = 1.0/len(bottom)
centrality = dict((n,d*s) for n,d in G.degree_iter(top))
s = 1.0/len(top)
centrality.update(dict((n,d*s) for n,d in G.degree_iter(bottom)))
return centrality
|
The above function is invoked using the networkx library and once the library is installed, you can eventually use it and the following code has to be written in python for the implementation of the Degree centrality of a node.
import networkx as nx
G=nx.erdos_renyi_graph(100,0.5)
d=nx.degree_centrality(G)
print(d)
|
The result is as follows:
{0: 0.5252525252525253, 1: 0.4444444444444445, 2: 0.5454545454545455, 3: 0.36363636363636365,
4: 0.42424242424242425, 5: 0.494949494949495, 6: 0.5454545454545455, 7: 0.494949494949495,
8: 0.5555555555555556, 9: 0.5151515151515152, 10: 0.5454545454545455, 11: 0.5151515151515152,
12: 0.494949494949495, 13: 0.4444444444444445, 14: 0.494949494949495, 15: 0.4141414141414142,
16: 0.43434343434343436, 17: 0.5555555555555556, 18: 0.494949494949495, 19: 0.5151515151515152,
20: 0.42424242424242425, 21: 0.494949494949495, 22: 0.5555555555555556, 23: 0.5151515151515152,
24: 0.4646464646464647, 25: 0.4747474747474748, 26: 0.4747474747474748, 27: 0.494949494949495,
28: 0.5656565656565657, 29: 0.5353535353535354, 30: 0.4747474747474748, 31: 0.494949494949495,
32: 0.43434343434343436, 33: 0.4444444444444445, 34: 0.5151515151515152, 35: 0.48484848484848486,
36: 0.43434343434343436, 37: 0.4040404040404041, 38: 0.5656565656565657, 39: 0.5656565656565657,
40: 0.494949494949495, 41: 0.5252525252525253, 42: 0.4545454545454546, 43: 0.42424242424242425,
44: 0.494949494949495, 45: 0.595959595959596, 46: 0.5454545454545455, 47: 0.5050505050505051,
48: 0.4646464646464647, 49: 0.48484848484848486, 50: 0.5353535353535354, 51: 0.5454545454545455,
52: 0.5252525252525253, 53: 0.5252525252525253, 54: 0.5353535353535354, 55: 0.6464646464646465,
56: 0.4444444444444445, 57: 0.48484848484848486, 58: 0.5353535353535354, 59: 0.494949494949495,
60: 0.4646464646464647, 61: 0.5858585858585859, 62: 0.494949494949495, 63: 0.48484848484848486,
64: 0.4444444444444445, 65: 0.6262626262626263, 66: 0.5151515151515152, 67: 0.4444444444444445,
68: 0.4747474747474748, 69: 0.5454545454545455, 70: 0.48484848484848486, 71: 0.5050505050505051,
72: 0.4646464646464647, 73: 0.4646464646464647, 74: 0.5454545454545455, 75: 0.4444444444444445,
76: 0.42424242424242425, 77: 0.4545454545454546, 78: 0.494949494949495, 79: 0.494949494949495,
80: 0.4444444444444445, 81: 0.48484848484848486, 82: 0.48484848484848486, 83: 0.5151515151515152,
84: 0.494949494949495, 85: 0.5151515151515152, 86: 0.5252525252525253, 87: 0.4545454545454546,
88: 0.5252525252525253, 89: 0.5353535353535354, 90: 0.5252525252525253, 91: 0.4646464646464647,
92: 0.4646464646464647, 93: 0.5555555555555556, 94: 0.5656565656565657, 95: 0.4646464646464647,
96: 0.494949494949495, 97: 0.494949494949495, 98: 0.5050505050505051, 99: 0.5050505050505051}
The above result is a dictionary depicting the value of degree centrality of each node. The above is an extension of my article series on the centrality measures. Keep networking!!!
References
You can read more about the same at
https://en.wikipedia.org/wiki/Centrality#Degree_centrality
http://networkx.readthedocs.io/en/networkx-1.10/index.html
Share your thoughts in the comments
Please Login to comment...