Betweenness Centrality (Centrality Measure)

In graph theory, betweenness centrality is a measure of centrality in a graph based on shortest paths. For every pair of vertices in a connected graph, there exists at least one shortest path between the vertices such that either the number of edges that the path passes through (for unweighted graphs) or the sum of the weights of the edges (for weighted graphs) is minimized. 

The betweenness centrality for each vertex is the number of these shortest paths that pass through the vertex. Betweenness centrality finds wide application in network theory: it represents the degree of which nodes stand between each other. For example, in a telecommunications network, a node with higher betweenness centrality would have more control over the network, because more information will pass through that node. Betweenness centrality was devised as a general measure of centrality: it applies to a wide range of problems in network theory, including problems related to social networks, biology, transport and scientific cooperation. 

Definition

The betweenness centrality of a node {\displaystyle v} v is given by the expression:

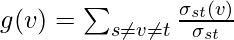
where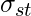is the total number of shortest paths from node 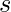to node 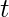and 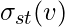is the number of those paths that pass through . 

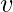Note that the betweenness centrality of a node scales with the number of pairs of nodes as implied by the summation indices. Therefore, the calculation may be rescaled by dividing through by the number of pairs of nodes not including 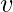, so that . The division is done by 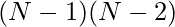for directed graphs and 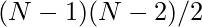for undirected graphs, where 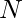is the number of nodes in the giant component. Note that this scales for the highest possible value, where one node is crossed by every single shortest path. This is often not the case, and a normalization can be performed without a loss of precision

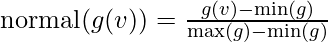
which results in: 

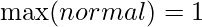
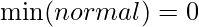
Note that this will always be a scaling from a smaller range into a larger range, so no precision is lost. 

Weighted Networks

In a weighted network the links connecting the nodes are no longer treated as binary interactions, but are weighted in proportion to their capacity, influence, frequency, etc., which adds another dimension of heterogeneity within the network beyond the topological effects. A node’s strength in a weighted network is given by the sum of the weights of its adjacent edges.

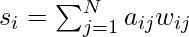
With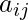and 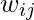being adjacency and weight matrices between nodes 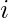and 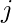, respectively. Analogous to the power law distribution of degree found in scale free networks, the strength of a given node follows a power law distribution as well. 

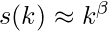
A study of the average value 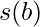of the strength for vertices with betweenness 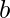shows that the functional behavior can be approximated by a scaling form

.

Following is the code for the calculation of the betweenness centrality of the graph and its various nodes. 

Implementation:

Python

def betweenness_centrality(G, k=None, normalized=True, weight=None,
                        endpoints=False, seed=None):
    r"""Compute the shortest-path betweenness centrality for nodes.

    Betweenness centrality of a node $v$ is the sum of the
    fraction of all-pairs shortest paths that pass through $v$

    .. math::

    c_B(v) =\sum_{s,t \in V} \frac{\sigma(s, t|v)}{\sigma(s, t)}

    where $V$ is the set of nodes, $\sigma(s, t)$ is the number of
    shortest $(s, t)$-paths, and $\sigma(s, t|v)$ is the number of
    those paths passing through some node $v$ other than $s, t$.
    If $s = t$, $\sigma(s, t) = 1$, and if $v \in {s, t}$,
    $\sigma(s, t|v) = 0$ [2]_.

    Parameters
    ----------
    G : graph
    A NetworkX graph.

    k : int, optional (default=None)
    If k is not None use k node samples to estimate betweenness.
    The value of k <= n where n is the number of nodes in the graph.
    Higher values give better approximation.

    normalized : bool, optional
    If True the betweenness values are normalized by `2/((n-1)(n-2))`
    for graphs, and `1/((n-1)(n-2))` for directed graphs where `n`
    is the number of nodes in G.

    weight : None or string, optional (default=None)
    If None, all edge weights are considered equal.
    Otherwise holds the name of the edge attribute used as weight.

    endpoints : bool, optional
    If True include the endpoints in the shortest path counts.

    Returns
    -------
    nodes : dictionary
    Dictionary of nodes with betweenness centrality as the value.


    Notes
    -----
    The algorithm is from Ulrik Brandes [1]_.
    See [4]_ for the original first published version and [2]_ for details on
    algorithms for variations and related metrics.

    For approximate betweenness calculations set k=#samples to use
    k nodes ("pivots") to estimate the betweenness values. For an estimate
    of the number of pivots needed see [3]_.

    For weighted graphs the edge weights must be greater than zero.
    Zero edge weights can produce an infinite number of equal length
    paths between pairs of nodes.


    """
    betweenness = dict.fromkeys(G, 0.0) # b[v]=0 for v in G
    if k is None:
        nodes = G
    else:
        random.seed(seed)
        nodes = random.sample(G.nodes(), k)
    for s in nodes:

        # single source shortest paths
        if weight is None: # use BFS
            S, P, sigma = _single_source_shortest_path_basic(G, s)
        else: # use Dijkstra's algorithm
            S, P, sigma = _single_source_dijkstra_path_basic(G, s, weight)

        # accumulation
        if endpoints:
            betweenness = _accumulate_endpoints(betweenness, S, P, sigma, s)
        else:
            betweenness = _accumulate_basic(betweenness, S, P, sigma, s)

    # rescaling
    betweenness = _rescale(betweenness, len(G), normalized=normalized,
                        directed=G.is_directed(), k=k)
    return betweenness

The above function is invoked using the networkx library and once the library is installed, you can eventually use it and the following code has to be written in python for the implementation of the betweenness centrality of a node. 

Python

>>> import networkx as nx
>>> G=nx.erdos_renyi_graph(50,0.5)
>>> b=nx.betweenness_centrality(G)
>>> print(b)

The result of it is: 

{0: 0.01220586070437195, 1: 0.009125402885768874, 2: 0.010481510111098788, 3: 0.014645690907182346, 
4: 0.013407129955492722, 5: 0.008165902336070403, 6: 0.008515486873573529, 7: 0.0067362883337957575, 
8: 0.009167651113672941, 9: 0.012386122359980324, 10: 0.00711685931010503, 11: 0.01146358835858978, 
12: 0.010392276809830674, 13: 0.0071149912635190965, 14: 0.011112503660641336, 15: 0.008013362669468532,
16: 0.01332441710128969, 17: 0.009307485134691016, 18: 0.006974541084171777, 19: 0.006534636068324543, 
20: 0.007794762718607258, 21: 0.012297442232146375, 22: 0.011081427155225095, 23: 0.018715475770172643,
24: 0.011527827410298818, 25: 0.012294312339823964, 26: 0.008103941622217354, 27: 0.011063824792934858,
28: 0.00876321613116331, 29: 0.01539738650994337, 30: 0.014968892689224241, 31: 0.006942569786325711,
32: 0.01389881951343378, 33: 0.005315473883526104, 34: 0.012485048548223817, 35: 0.009147849010405877,
36: 0.00755662592209711, 37: 0.007387027127423285, 38: 0.015993065123210606, 39: 0.0111516804297535,
40: 0.010720274864419366, 41: 0.007769933231367805, 42: 0.009986222659285306, 43: 0.005102869708942402,
44: 0.007652686310399397, 45: 0.017408689421606432, 46: 0.008512679806690831, 47: 0.01027761151708757, 
48: 0.008908600658162324, 49: 0.013439198921385216}

The above result is a dictionary depicting the value of betweenness centrality of each node. The above is an extension of my article series on the centrality measures. Keep networking!!! 

If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.