Katz Centrality (Centrality Measure)
Last Updated :
28 Jul, 2022
In graph theory, the Katz centrality of a node is a measure of centrality in a network. It was introduced by Leo Katz in 1953 and is used to measure the relative degree of influence of an actor (or node) within a social network. Unlike typical centrality measures which consider only the shortest path (the geodesic) between a pair of actors, Katz centrality measures influence by taking into account the total number of walks between a pair of actors.
It is similar to Google’s PageRank and to the eigenvector centrality.
Measuring Katz centrality
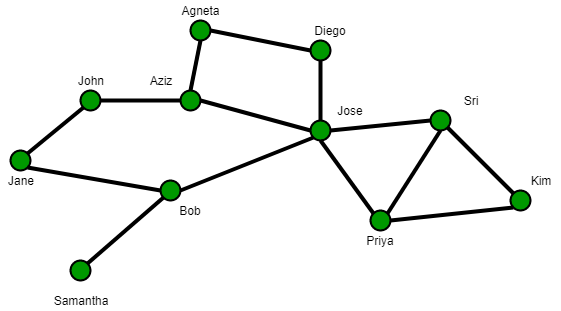
A simple social network: the nodes represent people or actors and the edges between nodes represent some relationship between actors
Katz centrality computes the relative influence of a node within a network by measuring the number of the immediate neighbors (first degree nodes) and also all other nodes in the network that connect to the node under consideration through these immediate neighbors. Connections made with distant neighbors are, however, penalized by an attenuation factor 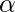 . Each path or connection between a pair of nodes is assigned a weight determined by
. Each path or connection between a pair of nodes is assigned a weight determined by  and the distance between nodes as
and the distance between nodes as  .
.
For example, in the figure on the right, assume that John’s centrality is being measured and that  . The weight assigned to each link that connects John with his immediate neighbors Jane and Bob will be
. The weight assigned to each link that connects John with his immediate neighbors Jane and Bob will be 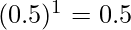 . Since Jose connects to John indirectly through Bob, the weight assigned to this connection (composed of two links) will be
. Since Jose connects to John indirectly through Bob, the weight assigned to this connection (composed of two links) will be  . Similarly, the weight assigned to the connection between Agneta and John through Aziz and Jane will be
. Similarly, the weight assigned to the connection between Agneta and John through Aziz and Jane will be  and the weight assigned to the connection between Agneta and John through Diego, Jose and Bob will be
and the weight assigned to the connection between Agneta and John through Diego, Jose and Bob will be  .
.
Mathematical formulation
Let A be the adjacency matrix of a network under consideration. Elements 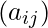 of A are variables that take a value 1 if a node i is connected to node j and 0 otherwise. The powers of A indicate the presence (or absence) of links between two nodes through intermediaries. For instance, in matrix
of A are variables that take a value 1 if a node i is connected to node j and 0 otherwise. The powers of A indicate the presence (or absence) of links between two nodes through intermediaries. For instance, in matrix 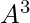 , if element
, if element 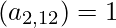 , it indicates that node 2 and node 12 are connected through some first and second degree neighbors of node 2. If
, it indicates that node 2 and node 12 are connected through some first and second degree neighbors of node 2. If 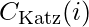 denotes Katz centrality of a node i, then mathematically:
denotes Katz centrality of a node i, then mathematically:
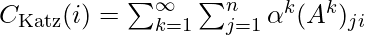
Note that the above definition uses the fact that the element at location 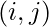 of the adjacency matrix
of the adjacency matrix 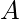 raised to the power
raised to the power 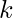 (i.e.
(i.e. 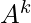 ) reflects the total number of
) reflects the total number of 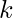 degree connections between nodes
degree connections between nodes 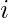 and
and 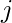 . The value of the attenuation factor
. The value of the attenuation factor 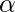 has to be chosen such that it is smaller than the reciprocal of the absolute value of the largest eigenvalue of the adjacency matrix A. In this case the following expression can be used to calculate Katz centrality:
has to be chosen such that it is smaller than the reciprocal of the absolute value of the largest eigenvalue of the adjacency matrix A. In this case the following expression can be used to calculate Katz centrality:
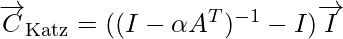
Here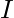 is the identity matrix,
is the identity matrix, 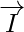 is an identity vector of size n (n is the number of nodes) consisting of ones.
is an identity vector of size n (n is the number of nodes) consisting of ones. 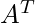 denotes the transposed matrix of A and (
denotes the transposed matrix of A and (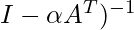 denotes matrix inversion of the term (
denotes matrix inversion of the term ( ).
).
Following is the code for the calculation of the Katz Centrality of the graph and its various nodes.
Implementation:
Python
def katz_centrality(G, alpha=0.1, beta=1.0,
max_iter=1000, tol=1.0e-6,
nstart=None, normalized=True,
weight = 'weight'):
from math import sqrt
if len(G) == 0:
return {}
nnodes = G.number_of_nodes()
if nstart is None:
x = dict([(n,0) for n in G])
else:
x = nstart
try:
b = dict.fromkeys(G,float(beta))
except (TypeError,ValueError,AttributeError):
b = beta
if set(beta) != set(G):
raise nx.NetworkXError('beta dictionary '
'must have a value for every node')
for i in range(max_iter):
xlast = x
x = dict.fromkeys(xlast, 0)
for n in x:
for nbr in G[n]:
x[nbr] += xlast[n] * G[n][nbr].get(weight, 1)
for n in x:
x[n] = alpha*x[n] + b[n]
err = sum([abs(x[n]-xlast[n]) for n in x])
if err < nnodes*tol:
if normalized:
try:
s = 1.0/sqrt(sum(v**2 for v in x.values()))
except ZeroDivisionError:
s = 1.0
else:
s = 1
for n in x:
x[n] *= s
return x
raise nx.NetworkXError('Power iteration failed to converge in '
'%d iterations.' % max_iter)
|
The above function is invoked using the networkx library and once the library is installed, you can eventually use it and the following code has to be written in python for the implementation of the katz centrality of a node.
Python
>>> import networkx as nx
>>> import math
>>> G = nx.path_graph(4)
>>> phi = (1+math.sqrt(5))/2.0
>>> centrality = nx.katz_centrality(G,1/phi-0.01)
>>> for n,c in sorted(centrality.items()):
... print("%d %0.2f"%(n,c))
|
The output of the above code is:
0 0.37
1 0.60
2 0.60
3 0.37
The above result is a dictionary depicting the value of katz centrality of each node. The above is an extension of my article series on the centrality measures. Keep networking!!!
Share your thoughts in the comments
Please Login to comment...