Data mining is the process of collecting and processing data from a heap of unprocessed data. When the patterns are established, various relationships between the datasets can be identified and they can be presented in a summarized format which helps in statistical analysis in various industries. Among the other data structures, the graph is widely used in modeling advanced structures and patterns. In data mining, the graph is used to find subgraph patterns for discrimination, classification, clustering of data, etc. The graph is used in network analysis. By linking the various nodes, graphs form network-like communications, web and computer networks, social networks, etc. In multi-relational data mining, graphs or networks is used because of the varied interconnected relationship between the datasets in a relational database.
Graph mining
Graph mining is a process in which the mining techniques are used in finding a pattern or relationship in the given real-world collection of graphs. By mining the graph, frequent substructures and relationships can be identified which helps in clustering the graph sets, finding a relationship between graph sets, or discriminating or characterizing graphs. Predicting these patterning trends can help in building models for the enhancement of any application that is used in real-time. To implement the process of graph mining, one must learn to mine frequent subgraphs.
Frequent Subgraph Mining
Let us consider a graph h with an edge set E(h) and a vertex set V(h). Let us consider the existence of subgraph isomorphism from h to h’ in such a way that h is a subgraph of h’. A label function is a function that plots either the edges or vertices to a label. Let us consider a labeled graph dataset, 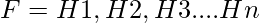 Let us consider s(h) as the support which means the percentage of graphs in F where h is a subgraph. A frequent graph has support that will be no less than the minimum support threshold. Let us denote it as min_support.
Let us consider s(h) as the support which means the percentage of graphs in F where h is a subgraph. A frequent graph has support that will be no less than the minimum support threshold. Let us denote it as min_support.
Steps in finding frequent subgraphs:
There are two steps in finding frequent subgraphs.
- The first step is to create frequent substructure candidates.
- The second step is to find the support of each and every candidate. We must optimize and enhance the first step because the second step is an NP-completed set where the computational complexity is accurate and high.
There are two methods for frequent substructure mining.
The Apriori-based approach: The approach to find the frequent graphs begin from the graph with a small size. The approach advances in a bottom-up way by creating candidates with extra vertex or edge. This algorithm is called an Apriori Graph. Let us consider Qk as the frequent sub-structure set with a size of k. This approach acquires a level-wise mining technique. Before the Apriori Graph technique, the generation of candidates must be done. This is done by combining two same but slightly varied frequent subgraphs. After the formation of new substructures, the frequency of the graph is checked. Out of that, the graphs found frequently are used to create the next candidate. This step to generate frequent substructure candidates is a complex step. But, when it comes to generating candidates in itemset, it is easy and effortless. Let’s consider an example of having two itemsets of size three such that 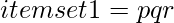 and
and 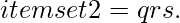 So, the itemset derived using join would be pqrs. But when it comes to substructures, there is more than one method to join two substructures.
So, the itemset derived using join would be pqrs. But when it comes to substructures, there is more than one method to join two substructures.
Algorithm:
This approach is based on frequent substructure mining.
Input:
F= a graph data set.
min_support= minimum support threshold
Output:
Q1,Q2,Q3,....QK,
a frequent substructure set graphs with the size range from 1 to k.
Q1 <- all the frequent 1 subgraphs in F;
k <- 2;
while Qk-1 ≠ ∅ do
Qk <- ∅;
Gk <- candidate_generation(Qk-1);
foreach candidate l ∈ Gk do
l.count <- 0;
foreach Fi ∈ F do
if isomerism_subgraph(l,Fi) then
l.count <- l.count+1;
end
end
if l.count ≥ min_support(F) ∧ l∉Qk then
Qk = Qk U l;
end
end
k <- k+1;
endIt is an iterative method in which the first candidate generation takes place followed by the support computation. The subgraphs are generated using subgraph isomorphism. Thus frequent subgraphs are generated by efficiently using this approach which helps in FSM. Apriori approach uses BFS(Breadth-First Search) due to the iterative level-wise generation of candidates. This is necessary because if you want to mine the k+1 graph, you should have already mined till k subgraphs.
The Pattern- growth approach: This pattern-growth approach can use both BFS and DFS(Depth First Search). DFS is preferred for this approach due to its less memory consumption nature. Let us consider a graph h. A new graph can be formed by adding an edge e. The edge can introduce a vertex but it is not a need. If it introduces a vertex, it can be done in two ways, forward and backward. The Pattern-growth graph is easy but it is not that efficient. Because there is a possibility of creating a similar graph that is already created which leads to computation inefficiency. The duplicate graphs generated can be removed but it increases the time and work. To avoid the creation of duplicate graphs, the frequent graphs should be introduced very carefully and conservatively which calls the need for other algorithms.
Algorithm:
The below algorithm is a pattern-growth-based frequent substructure mining with a simplistic approach. If you need to search without duplicating, you must go with a different algorithm with gSpan.
Input:
q= a frequent graph
F= a graph data set.
min_support= minimum support threshold
Output:
P = the frequent graph set
P <- ∅;
Call patterngrow_graph(q, F, min_support, P);
procedure patterngrow_graph(q, F, min_support, P)
if q ∈ P then return;
else insert q into P;
scan F once, find all the edges e such that q can be extended to q -> e;
for each frequent q -> e do
PatternGrowthGraph(q -> e, D, min_support, P);
return;
An edge e is used to extend a new graph from the old one q. The newly extend graph is denoted as  The extension can either be backward or forward.
The extension can either be backward or forward.
Constraint-based substructure mining
According to the request of the user, the constraints described changes in the mining process. But, if we generalize and categorize them into specific constraints, the mining process would be handled easily by pushing them into the given frameworks. constraint-pushing strategy is used in pattern growth mining tasks. Let’s see some important constraint categories.
- Subgraph containment constraint: When a user requests a pattern with specified subgraphs, this constraint is used. This constraint is also called a set containment constraint. The given set of subgraphs is taken as a query and then mining is done based on the chosen data by extending the patterns from the subgraph sets. This technique can be used to mine when the user requests patterns with specific sets of edges or vertices.
- Value- sum constraint: Here, the constraint is the sum of weights on the edges. There are two ranges high and low. The two constraints are designated as
 and
and 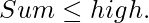 The first condition is called monotonic constraint because once the condition is satisfied, still the extension can take place by adding edges until the next condition is satisfied. But the latter condition is called anti-monotonic constraint because once the condition becomes satisfied, further no more extension can be made. By this method, the constraint-pushing technique will work out well.
The first condition is called monotonic constraint because once the condition is satisfied, still the extension can take place by adding edges until the next condition is satisfied. But the latter condition is called anti-monotonic constraint because once the condition becomes satisfied, further no more extension can be made. By this method, the constraint-pushing technique will work out well. - Geometric Constraint: In this constraint, the angle between pair of edges within a given range that is connected is taken. Let us consider a graph h, such that
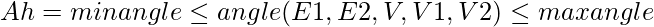 where E1, E2 are the edges connected at the vertex V and connected to the other two vertices at the other two ends V1, V2. Ah is called the anti-monotonic constraint because if any one of the angles formed by combining two edges didn’t satisfy, it does not move to the next level and it will never satisfy Ah. It can be pushed to the edge extension process and eliminate any extension that doesn’t satisfy Ah.
where E1, E2 are the edges connected at the vertex V and connected to the other two vertices at the other two ends V1, V2. Ah is called the anti-monotonic constraint because if any one of the angles formed by combining two edges didn’t satisfy, it does not move to the next level and it will never satisfy Ah. It can be pushed to the edge extension process and eliminate any extension that doesn’t satisfy Ah.
Network Analysis
In the concept of network analysis, the relationship between the units is called links in a graph. From the data mining outlook, this is called link mining or link analysis. The network is a diversional dataset with a multi-relational concept in form of a graph. The graph is very large with nodes as objects, edges as links which in turn denote the relationship between the nodes or objects. Telephone networking systems, WWW( World Wide Web) are very good examples. It also helps in filtering the datasets and providing customer-preferred services. Every network consists of numerous nodes. The datasets are widely enormous. Thus by studying and mining useful information from a wide group of datasets would help in solving problems and effective transmission of data.
Link Mining
There are some conventional methods of machine learning in which taking homogeneous objects from one relationship is taken. But in networks, this is not applicable due to a large number of nodes and its multi-relational, heterogeneous nature. Thus the link mining has appeared as a new field after many types of research. Link mining is the convergence of multiple research held in graph mining, networks, hypertexts, logic programming, link analysis, predictive analysis, and modeling. Links are nothing but the relationship between nodes in a network. With the help of links, the mining process can be held efficiently. This calls for the various functions to be done.
- Link-based object classification: In link mining, only attributes are not enough. Here the links and the traits of the linked nodes are also necessary. One best example is Web-based classification. In web-based classification, the system predicts the categorization of a webpage based on the presence of that specified word which means the searched word occurs on that page. Anchor text is which the person clicks the hyperlink that opens while searching. These two things act as attributes in web-based classification. The attributes can be anything that relates to the link and network pages.
- Link type prediction: According to the resources of the object involved, the system predicts the motive of that link. In organizations, it helps in suggesting interactive communication sessions between employees if needed. In the online retail market, it helps predict what a customer prefers to buy which can increase sales and recommendations.
- Object type prediction: Here the prediction is based on the type of the object involved, its attributes and properties, links and traits of the object linked to it. For example in the restaurant domain, a similar method is done to predict if a customer prefers ordering food or directly visiting the restaurant. It also helps in predicting the method of communication a customer prefers whether by phone or mail.
- Link Cardinality estimation: In this task, there are two types of estimation. The first one is predicting the number of links linked to an object. For example, the percentage of the authority of a web page can be calculated by finding the number of links linked to it which is called in-links. Web pages that act as a hub which means a set of web pages denotes other links which come under the same topic can be identified using out-links. For example, when a pandemic strikes, finding the links of the affected patient can lead us to the other patients which helps in the control of the transmission. The second one is done by predicting the number of objects outreaching along a route from an object. This method is crucial in estimating the object number returned as output by a query.
- Predicting link existence: In link type prediction, the type of the link is predicted. But, here the system predicts whether a link exists between two objects. For an instance, this task is used to predict if a link exists between two web pages.
- Object Reconciliation: In this method, the function is to predict if any two objects are the same on the basis of their attributes or traits or links. This method is also called identity uncertainty or record linkage. This task has it’s the same procedure in the matching of citation, extraction of details, getting rid of duplicates, consolidating objects. For an instance, this task is to help if one website is reflecting the other website like a mirror to each other.
Challenges in Link Mining
- Statistical compared to logical dependencies: The logical relationship between objects is denoted by graph-link structures. The statistical relationship is denoted by probabilistic dependencies. The rational handling of these two dependencies is difficult in data mining which is multi-relational. One must be careful enough to find the logical dependencies between objects along with probabilistic relationships between attributes. These dependencies take a large amount of space which complicates the mathematical model deployed.
- Collective classification and consolidation: Let us consider a training model based on objects that are class-labeled. In conventional classification, classification is only done based on the attribute. If there is a chance that classification occurs after giving training with unlabeled objects, the model becomes incapable of classification due to the complications of the correlations of the objects. This calls for the need for another supplementary iterative step which consolidates the labels of objects based on the labels of objects linked to it. Here collective classification takes place.
- Constructive use of labeled and unlabeled data: One emerging technique is to merge both labeled and unlabeled data. Unlabeled data assist in identifying the distribution of attributes. The links that are present in unlabeled data help us in extracting the linked object’s attributes. The links that are present between unlabeled and labeled data help in establishing dependencies which increases the efficiency in interference.
- Open compared to closed-world assumptions: In the conventional method, it is assumed that we know all the possible objects/ entities present in the domain which is closed-world assumptions. But, closed world assumption is impractical in the application of reality. This calls for the introduction of specific language for probability distributions with respect to relational objects that contains a varied set of objects.
Community Mining
Network analysis includes the finding of objects which are in groups that share similar attributes. This process is known as community mining. In the web page linkage, the introduction of community where a group of web pages is made which follow a common theme. Many community mining algorithms decide that there is only one network and it tries to establish a homogeneous relationship. But in the real world web pages, there are multiple networks with heterogeneous relationships. This proves the need for multi-relational community mining.
Share your thoughts in the comments
Please Login to comment...