Cosine Similarity
Last Updated :
15 Jul, 2023
Prerequisite – Measures of Distance in Data Mining In Data Mining, similarity measure refers to distance with dimensions representing features of the data object, in a dataset. If this distance is less, there will be a high degree of similarity, but when the distance is large, there will be a low degree of similarity. Some of the popular similarity measures are –
- Euclidean Distance.
- Manhattan Distance.
- Jaccard Similarity.
- Minkowski Distance.
- Cosine Similarity.
Cosine similarity is a metric, helpful in determining, how similar the data objects are irrespective of their size. We can measure the similarity between two sentences in Python using Cosine Similarity. In cosine similarity, data objects in a dataset are treated as a vector. The formula to find the cosine similarity between two vectors is –
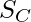 (x, y) = x . y / ||x||
(x, y) = x . y / ||x|| 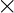 ||y||
||y||
where,
- x . y = product (dot) of the vectors ‘x’ and ‘y’.
- ||x|| and ||y|| = length (magnitude) of the two vectors ‘x’ and ‘y’.
- ||x||
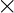 ||y|| = regular product of the two vectors ‘x’ and ‘y’.
||y|| = regular product of the two vectors ‘x’ and ‘y’.
Example : Consider an example to find the similarity between two vectors – ‘x’ and ‘y’, using Cosine Similarity. The ‘x’ vector has values, x = { 3, 2, 0, 5 } The ‘y’ vector has values, y = { 1, 0, 0, 0 } The formula for calculating the cosine similarity is : 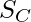 (x, y) = x . y / ||x||
(x, y) = x . y / ||x|| 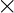 ||y||
||y||
x . y = 3*1 + 2*0 + 0*0 + 5*0 = 3
||x|| = √ (3)^2 + (2)^2 + (0)^2 + (5)^2 = 6.16
||y|| = √ (1)^2 + (0)^2 + (0)^2 + (0)^2 = 1
∴ 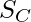 (x, y) = 3 / (6.16 * 1) = 0.49
(x, y) = 3 / (6.16 * 1) = 0.49
The dissimilarity between the two vectors ‘x’ and ‘y’ is given by –
∴ 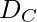 (x, y) = 1 -
(x, y) = 1 - 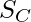 (x, y) = 1 - 0.49 = 0.51
(x, y) = 1 - 0.49 = 0.51
- The cosine similarity between two vectors is measured in ‘θ’.
- If θ = 0°, the ‘x’ and ‘y’ vectors overlap, thus proving they are similar.
- If θ = 90°, the ‘x’ and ‘y’ vectors are dissimilar.
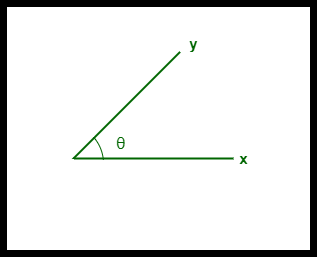
Cosine Similarity between two vectors
Advantages :
- The cosine similarity is beneficial because even if the two similar data objects are far apart by the Euclidean distance because of the size, they could still have a smaller angle between them. Smaller the angle, higher the similarity.
- When plotted on a multi-dimensional space, the cosine similarity captures the orientation (the angle) of the data objects and not the magnitude.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...