Concurrent Lines occur when three or more lines intersect at a single point. This concept is a significant topic within the realm of straight lines. In this article on Concurrent Lines, we will delve into the precise definition of concurrent lines, explore the conditions that lead to concurrent lines, examine the role of concurrent lines within triangles, distinguish concurrent lines from intersecting lines, and solve some practice problems to get a better understanding of the topic.
Meaning of Concurrent Lines
Concurrent lines are a set of three or more straight lines that intersect at a common point. The point at which they intersect is called the point of concurrency. Concurrent lines are always going to be non-parallel and the number of lines passing through the point of concurrency must be equal to or greater than three. If the number of lines intersecting at a common point is only two then it is considered as an intersecting line.
Concurrent Lines Definition
Three or more lines are said to be Concurrent if they all pass through a common point, which is known as a point of concurrency.
Point of Concurrency
Point of Concurrency is a term used to describe a point where three or more lines, rays or line segments intersect. In simple words, a point of intersection of concurrent lines is known as a Point of Concurrency.
.png)
Concurrent Lines
In various geometric shapes, different types of points of concurrency can be identified. Some well-known points of concurrency for triangles are:
- Incenter
- Circumcenter
- Orthocenter
- Centroid
We will these points further in the article.
Examples of Concurrent Lines
We know that any three lines with a common intersection point are called concurrent lines. These concurrent lines are also present in various geometrical shapes. Let’s see examples of such concurrent lines.
- Circle: Lines passing through the center of a circle i.e. all the diameters are concurrent.
- Quadrilateral: Lines segments joining midpoints of opposite sides, and the diagonals are passing through the common point.

Triangle: Line segments that pass through the vertex and meet at a common point is one of the examples of concurrent lines in a triangle.
.png)
Example: Point of Concurrency in Triangle
Condition for Three Lines to be Concurrent
There are two conditions for three lines to be concurrent. First is if the determinant of the coefficients of the equations of the line is zero then line is concurrent and second is solving two equations of lines and putting the value of x and y in the third equation and checking if LHS = RHS. Let’s learn these methods in detail.
Condition 1: Determinant Method
If three lines are considered concurrent, it means that the point where two of these lines intersect also lies on the line.
Assume the equation of three lines as:
a1x + b1y + c1 = 0 ………….(i)
a2x + b2y + c2 = 0 ………….(ii)
a3x + b3y + c3 = 0 ………….(iii)
The criterion that determines whether three lines are concurrent can be expressed as follows:
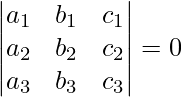
OR
a1(b2c3 – c2b3) – b1(a2c3 – a3c2) + c1(a2b3 – a3b2) = 0
Condition 2: Substitution Method
If three lines are considered concurrent, it means that the point where two of these lines intersect also lies on the line. We can follow these steps to prove it.
Assume the equation of three lines as:
a1x + b1y + c1 = 0 ………….(i)
a2x + b2y + c2 = 0 ………….(ii)
a3x + b3y + c3 = 0 ………….(iii)
Step 1: Solve equations (i) and (ii) using the substitution method to get the values of x and y.
Step 2: Now put the values of x and y in equation (iii) if the final value becomes zero then the lines are concurrent else they are not concurrent.
Concurrent Lines, Line Segments and Rays
Line segments are lines that have a starting and an ending point. When a set of three or more line segments meet at a point is called a concurrent line segment.
Rays are a type of line that has only a single point and no endpoint. When a set of three or more rays meet at a point it is called a concurrent ray.
|
| has starting and ending point | only starting point | no starting point or ending point |
| length can be measured | length cannot be measured | length cannot be measured |
--1.png) Concurrent Line Segments | -2.png) Concurrent Rays | .png) Concurrent Lines |
Concurrent Lines vs Intersecting Lines
Intersecting lines are formed when only two lines are meeting at a common point. The point at which both lines meet is commonly known as Intersecting Point. It is important to note that this line can also be replaced with line segments or rays.
|
| exactly two | three or more than three |
| Intersecting point | Point of Concurrency |
.png) Intersecting lines | .png) Concurrent lines |
Concurrent Lines in a Triangle
A triangle is a 2D geometric shape that has three sides and angles. In a triangle, there are four most common sets of concurrent lines.
- Incenter: It is the point of intersection of three angular bisectors. Angular bisectors are lines that divide the interior angles of the triangle into two equal halves.
- Circumcenter: It is the point of intersection of three perpendicular bisectors. Perpendicular bisectors are the line that starts from the midpoint of a side making an angle of 90o.
- Orthocenter: It is the point of intersection of three altitudes. Altitudes are lines drawn from a vertex of the triangle perpendicular to the opposite side.
- Centroid: It is the point of intersection of the three medians. Medians connect each vertex of a triangle to the midpoint of the opposite side
.png)
Also, Read
Solved Examples on Concurrent Lines
Example 1: Prove the following set of three lines are concurrent. 15x – 18y + 1 = 0, 12x + 10y -3 = 0 and 6x + 66y – 11 = 0.
Solution:
Given:
15x – 18y + 1 = 0 …. (i)
12x + 10y – 3 = 0 ….(ii)
6x + 66y – 11 = 0 ….(iii)
Using Method 1
Determinant form is given as 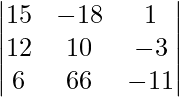
Solving the above determinant
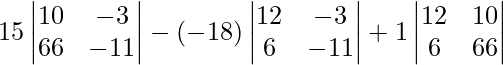
= 15(-110 + 198) + 18(-132 + 18) + 1(792-60)
= 0 .
Hence Proven, lines are concurrent.
Example 2: Find the value of c for which the three lines are concurrent 2x – 5y + 3 = 0, 5x – 9y + c = 0, x – 2y + 1 = 0 .
Solution:
Given
2x – 5y + 3 = 0 ……(i)
5x – 9y + c = 0 ……(ii)
x – 2y + 1 = 0 ……(iii)
(Using Method 2)
Step 1: solve equations (i) and (iii) using the substitution method
2x – 5y + 3 = 0
x – 2y + 1 = 0
upon solving we get x = 1 and y = 1
Step 2:Substitute the values in equation (ii).
5(1) – 9(1) + c = 0
c = 4
Example 3: Prove the following set of three lines are concurrent M1 = (a-b)x + (b-c)y + (c-a) = 0, M2 = (b – c)x + (c-a)y + (a-b) = 0, M3 = (c-a)x + (a-b)y + (b-c) = 0.
Solution:
Given:
M1 = (a – b)x + (b – c)y + (c – a) = 0 ….(i)
M2 = (b – c)x + (c – a)y + (a – b) = 0 ….(ii)
M3 = (c – a)x + (a – b)y + (b – c) = 0. ….(iii)
Determinant form,
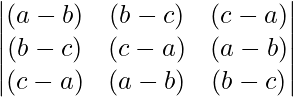
= (a – b)[(c – a)(b – c) – (a – b)(a – b)] – (b – c)[(b – c)(b – c) – (c – a)(a – b)] + (c – a)[(b -c)(a – b) – (c-a)(c – a)]
= (a – b)(c – a)(b – c) – (a – b)3 – (b – c)3 + (b – c)(c – a)(a – b) + (c – a)(b – c)(a – b) – (c – a)3
= 3 × (a – b)(b – c)(c – a) – (a – b)3 – (b-c)3 – (c-a)3
= 3 × (a – b)(b – c)(c – a) – 3a2(c − b) – 3b2(a − c) – 3c2(b − a)
= 0
Hence Proven, lines are concurrent.
Example 4: The following set of three lines are concurrent a1x + b1y + 1 = 0, a2x + b2y + 1 = 0, and a3x + b3y + 1 = 0. Prove that the points (a1 , b1), (a2 , b2), (a3 , b3) are collinear.
Solution:
If the following sets of lines are concurrent then there determinant must be
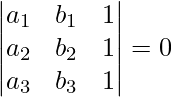
Now the above is also the condition for collinearity. Hence the given points (a1 , b1), (a2 , b2) , (a3 , b3) are collinear.
Practice Problems on Concurrent Lines
Q1. Prove the following set of three lines are concurrent 3x – 5y – 11 = 0, 5x + 3y -7 = 0 and x + 2y = 0.
Q2. Prove the following set of three lines are concurrent x = 0, y = 1, x = y.
Q3. Find the conditions at which these three lines meet at a common point y1 = m1x + c1, y2 = m2x + c2 and y3 = m3x +c3.
Q4. Find the conditions at which these three lines meet at a common point M1 = (a+b)x + cy + 1, M2 = (b+c)x + ay +1, M3 = (c+a)x + by + 1
FAQs on Concurrent Lines
1. What are Concurrent lines?
A set of three or more lines that meet a common point are called concurrent lines.
2. What is the Point of Concurrency?
The point at which concurrent lines pass throught is called the Point of Concurrency.
3. Why Parallels can’t be Concurrent?
Parallel lines never meet at any point hence they can never become concurrent
4. What is the difference between Concurrent Lines and Intersecting Lines?
When two lines meet at a common point then they are called intersecting lines but we need a minimum of three lines to meet at a common point to call it concurrent.
5. What are some Real-Life Applications of Concurrent Lines?
Concurrent lines have applications in various fields, including engineering, architecture, and art. For example, in architecture, they are used to determine the stability of structures. In engineering, concurrent forces acting on an object can be analyzed using concurrent lines.
Share your thoughts in the comments
Please Login to comment...