Class 9 RD Sharma Solutions – Chapter 5 Factorisation of Algebraic Expressions- Exercise 5.2 | Set 1
Last Updated :
23 Feb, 2021
Factorize each of the following expressions:
Question 1. p3+27
Solution:
⇒ p3+33
⇒(p+3)(p2-3p-9) [ a3+b3=(a+b)(a2-ab+b2) ]
Therefore, p3+27 = (p+3)(p2-3p-9)
Question 2. y3+125
Solution:
⇒ y3+53
⇒ (y+5)(y2-3y+25) [ a3+b3=(a+b)(a2-ab+b2) ]
Therefore, y3+125 = (y+5)(y2-3y+25)
Question 3. 1 – 27a3
Solution:
⇒ (1)3 – (3a)3
⇒ (1-3a)(12+3a+(3a)2) [ a3-b3=(a-b)(a2+ab+b2) ]
⇒ (1-3a)(1+3a+9a2)
Therefore, 1 – 27a3 = (1-3a)(1+3a+9a2)
Question 4. 8x3y3 +27a3
Solution:
⇒ (2xy)3 + (3a)3
⇒ (2xy+3a)((2xy)2 -2xy *3a +(3a)2) [ a3+b3=(a+b)(a2-ab+b2) ]
⇒ (2xy+3a)(4x2y2 -6xya +9a2)
Therefore, 8x3y3+27a3 = (2xy+3a)(4x2y2 -6xya +9a2)
Question 5. 64a3 – b3
Solution:
⇒ (4a)3 – b3
⇒ (4a – b ) ((4a)2 – 4a*b + b2) [ a3-b3=(a-b)(a2+ab+b2) ]
⇒ (4a – b ) (16a2 – 4a*b + b2)
Therefore, 64a3 – b3 = (4a – b ) (16a2 – 4a*b + b2)
Question 6. 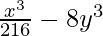
Solution:
⇒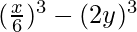
⇒ 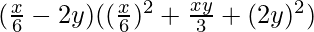 [ a3-b3=(a-b)(a2+ab+b2) ]
[ a3-b3=(a-b)(a2+ab+b2) ]
⇒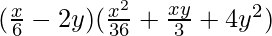
Therefore, 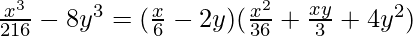
Question 7. 10x4y – 10xy4
Solution:
⇒ 10xy(x3-y3)
⇒ 10xy(x-y)(x2+xy+y2) [ a3-b3=(a-b)(a2+ab+b2) ]
Therefore, 10x4y – 10xy4 = 10xy(x-y)(x2+xy+y2)
Question 8. 54x6y+2x3y4
Solution:
⇒ 2x3y(27x3+y3)
⇒ 2x3y((3x)3+y3) [ a3+b3=(a+b)(a2-ab+b2) ]
⇒ 2x3y(3x+y)(9x2-3xy+y2)
Therefore, 54x6y+2x3y4 = 2x3y(3x+y)(9x2-3xy+y2)
Question 9. 32a3+108b3
Solution:
⇒ 4(8a3+27b3)
⇒ 4((2a)3+(3b)3)
⇒ 4 [ (2a+3b) ((2a)2 -6ab+(3b)2)] [ a3+b3=(a+b)(a2-ab+b2) ]
⇒ 4(2a+3b)(4a2 -6ab +3b2)
Therefore, 32a3+108b3 = 4(2a+3b)(4a2 -6ab +3b2)
Question 10. (a-2b)3-512b3
Solution:
⇒ (a-2b)3 – (8b)3
⇒ (a-2b-8b)((a-2b)2 – (a-2b)8b + (8b)2) [ a3-b3=(a-b)(a2+ab+b2) ]
⇒ (a – 10b)(a2 +4b2 -2ab +8ab + 16b2 +64b2)
⇒ (a – 10b)(a2 +52b2 +4ab)
Therefore, (a-2b)3-512b3 = (a – 10b)(a2 +52b2 +4ab)
Question 11. (a+b)3 -8(a-b)3
Solution:
⇒ (a+b)3 -[2(a-b)]3
⇒ (a+b)3 – (2a -2b)3
⇒ [a+b-(2a-2b)]((a+b)2+(a+b)(2a-2b)+(2a-2b)2 [a3-b3=(a-b)(a2+ab+b2) ]
⇒ (3b-a)[(a2+b2+2ab) +(2a2-2ab+2ab-2b2)+(4a2+4b2+8ab)]
⇒ (3b-a) [7a2+3b2 -6ab]
Therefore, (a+b)3 -8(a-b)3 = (3b-a) [7a2+3b2 -6ab]
Question 12. (x+2)3(x-2)3
Solution:
⇒ (x+2+x-2)((x+2)2 – (x+2)(x-2)+(x-2)2)
⇒ 2x(x2+4x+4-(x+2)(x-2)+x2-4x+4) [(a+b)(a-b)=a2-b2]
⇒2x(2x2+8-(x2-22))
⇒ 2x(x2 +8+4)
⇒ 2x(x2+12)
Therefore, (x+2)3(x-2)3 = 2x(x2+12)
Share your thoughts in the comments
Please Login to comment...