Class 9 NCERT Solutions- Chapter 13 Surface Areas And Volumes – Exercise 13.2
Last Updated :
28 Dec, 2020
Question 1. The curved surface area of a right circular cylinder of height 14 cm is 88 cm2. Find the diameter of the base of the cylinder.
Solution:
Given:
i) Height of cylinder(h)=14 cm
ii)Curved Surface Area of cylinder=88 cm2
Curved Surface Area = 2πrh
88 = 2*(22/7)*r*14
Hence, r=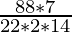
= 1 cm
As diameter=2*radius,
The diameter of the base of cylinder =2*1=2 cm
Question 2. It is required to make a closed cylindrical tank of height 1 m and base diameter 140 cm from a metal sheet. How many square meters of the sheet are required for the same?
Solution:
Given: i) Height of cylindrical tank (h)=1 m
ii) Base diameter of cylinder (d)=140 cm
iii) Radius of cylinder (r)=d/2=140/2=70cm=0.7 m
As metal sheet requirement for closed cylindrical tank is asked,
Area of metal sheet required =Total surface area of the cylindrical tank
= 2πr(r+h)
= 2*(22/7)*0.7*(0.7+1)
= 7.48 m2
Question 3. A metal pipe is 77 cm long. The inner diameter of a cross-section is 4 cm, the outer diameter being 4.4 cm. Find its (i) inner curved surface area, (ii) outer curved surface area, (iii) total surface area.
Solution:
We know that pipe has a hollow cylindrical structure
1) Height of Cylindrical metal pipe (h) =77 cm
2) The inner diameter of metal pipe (d)=4cm,
Hence, inner radius(r)=d/2=2 cm
3)The outer diameter of metal pipe (D)=4.4cm,
Hence, outer radius(R)=D/2=2.2 cm
i) Inner curved surface area=2πrh =2*(22/7)*2*77
=968 cm2
ii) Outer curved surface area=2πrh =2*(22/7)*2.2*77
=1064.8 cm2
iii) Total Surface Area=Inner curved surface area+Outer curved surface area+area of two bases
As pipe is hollow, area of two bases is a ring area given by=2(πR2-πr2) = 2π(R2-r2)
= 2* (22/7)*((2.2)2-(2)2)
= 5.28 cm2
Hence, Total surface area=968+1064.8+5.28=2038.08 cm2
Question 4. The diameter of a roller is 84 cm and its length is 120 cm. It takes 500 complete revolutions to move once over to level a playground. Find the area of the playground in m2.
Solution:
Roller is cylindrical in shape.
Diameter of a roller(d)=84 cm,
Hence, base radius of roller (r)=d/2=42cm =0.42 m
Height of cylinder(h)=Length of roller=120cm=1.2 m
Curved surface area of cylinder=2πrh =2*(22/7)*0.42*1.2 =3.168 m2
Revolutions done by roller=500
Hence, Area of playground= Curved surface area of roller*revolutions done by roller
= 3.168*500
=1584 m2
Question 5. A cylindrical pillar is 50 cm in diameter and 3.5 m in height. Find the cost of painting the curved surface of the pillar at the rate of ₹12.50 per m2.
Solution:
Diameter of cylindrical pillar=50 cm
Hence radius (r)=25cm=0.25 m
Height of cylindrical pillar (h)=3.5 m
Curved surface area of cylindrical pillar=2πrh=2*(22/7)*0.25*3.5
=5.50 m2
Rate of painting=₹12.50 per m2
Hence, cost of painting the curved surface of the pillar=5.50*12.50=₹68.75
Question 6 Curved surface area of a right circular cylinder is 4.4 m2. If the radius of the base of the cylinder is 0.7 m, find its height.
Solution:
Given: i) Radius of the base of cylinder(h)=0.7 m
ii)Curved Surface Area of cylinder=4.4 m2
Curved Surface Area =2πrh
4.4 =2*(22/7)*0.7*h
Hence, h=
= 1 m
Question 7. The inner diameter of a circular well is 3.5 m. It is 10 m deep. Find
(i) its inner curved surface area,
(ii) the cost of plastering this curved surface at the rate of ₹40 per m2.
Solution:
Well is cylindrical in nature.
Its inner diameter=3.5m, hence inner radius (r)=3.5/2=1.75 m
Its height (h)=10 m
i) Its inner curved surface area (A)=2πrh = 2*(22/7)*1.75*10
= 110 m2
ii) The cost of Plastering this inner curved surface = rate of plastering*A
= 40*110
= ₹4400
Question 8. In a hot water heating system, there is a cylindrical pipe of length 28 m and diameter 5 cm. Find the total radiating surface in the system.
Solution:
Length of cylindrical pipe (h)= 28m = 2800 cm
Diameter of cylindrical pipe=5 cm
Hence, radius of cylindrical pipe=5/2=2.5 cm
Cylindrical pipe radiates from curved surface only. Hence, we have to calculating radiating surface we have to measure curved surface area of that pipe.
Total radiating surface in the system = Curved surface area of pipe
= 2πrh
= 2*(22/7)*2.5*2800
= 44000 cm2
= 4.4 m2
Question 9. Find
(i) the lateral or curved surface area of a closed cylindrical petrol storage tank that is 4.2 m in diameter and 4.5 m high.
(ii) how much steel was actually used, if 1/12 of the steel actually used was wasted in making the tank.
Solution:
Diameter of cylindrical tank=4.2 m
Hence, radius of cylindrical tank (r)=4.2/2=2.1 m
Height of cylindrical tank (h)=4.5 m
i) Curved surface area of tank=2πrh = 2*(22/7)*2.1*4.5
= 59.4 m2
ii) As it is closed cylindrical tank,
Area of steel required to make = Total surface area of cylindrical tank
= 2πr(r+h)
= 2*(22/7)*2.1*(2.1+4.5)
= 87.12 m2 (1)
Let actually used steel =x m2. (1/2) of actually used steel was wasted.
Hence, tank is made up of 1-(1/12) = 11/12 part of steel. (2)
Hence, from (1) and (2), we get,
(11/12)x=87.12
i.e. x= = 95.04 m2
= 95.04 m2
Hence, 95.04 m2 steel was actually used to make tank.
Question 10. A cylindrical frame of a lampshade is to be covered with a decorative cloth. The frame has a base diameter of 20 cm and height of 30 cm. A margin of 2.5 cm is to be given for folding it over the top and bottom of the frame. Find how much cloth is required for covering the lampshade.
Solution:
Base diameter of frame=20 cm
Hence, base radius of frame=20/2=10 cm
Height of frame (including margins provided for folding frame over top and bottom of frame) = 30+2.5+2.5=35 cm
Cloth required for covering the lampshade= Curved surface area of lampshade
= 2πrh
= 2*(22/7)*10*35
= 2200 cm2
Question 11. The students of a Vidyalaya were asked to participate in a competition for making and decorating penholders in the shape of a cylinder with a base, using cardboard. Each penholder was to be of radius 3 cm and height 10.5 cm. The Vidyalaya was to supply the competitors with cardboard. If there were 35 competitors, how much cardboard was required to be bought for the competition?
Solution:
Penholder is in shape of a cylinder with a base. That is with curved surface with one base is to be created using cardboard.
Radius of penholder=3 cm
Height of penholder=10.5 cm
Area of cardboard required to make one penholder (A)
= Curved surface area of penholder + area of one base
= 2πrh+πr2
= 2*(22/7)*3*10.5+(22/7)*(3)2
= 198+28.28
= 226.28 cm2
Total area of Cardboard required to be bought for the competition
= Number of competitors* cardboard required for one penholder
= 35*226.28
= 7919.99 ≈ 7920 cm2
Share your thoughts in the comments
Please Login to comment...