Class 12 NCERT Solutions- Mathematics Part I – Chapter 6 Application of Derivatives – Exercise 6.4
Last Updated :
05 Mar, 2021
Question 1. Using differentials, find the approximate value of each of the following up to 3 places of decimal.
(i)√25.3
(ii)√49.5
(iii) √0.6
(iv) (0.009)1/3
(v) (0.999)1/10
(vi) (15)1/4
(vii) (26)1/3
(viii) (255)1/4
(ix) (82)1/4
(x) (401)1/2
(xi) (0.0037)1/2
(xii) (26.57)1/3
(xiii) (81.5)1/4
(xiv) (3.968)3/2
(xv) (32.15)1/5
Solution:
(i) √25.3
We take y = √x
Let x = 25 and △x = 0.3
△y = √(x +△x) – √x
= √25.3 – √25
= √25.3 – 5
or √25.3 = 5 + △y
Here, dy is approximately equal to △y
dy = (dy/dx)△x
= 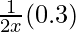
= 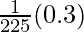
= 0.3/10
= 0.03
Hence, the approximate value of√25.3 = 5 + 0.03 = 5.03
(ii)√49.5
We take y = √x
Let x = 49 and △x = 0.5
△y = √(x +△x) – √x
= √49.5 – √49
= √49.5 – 7
or √49.5 = 7 + △y
Here, dy is approximately equal to △y
dy = (dy/dx)△x
= 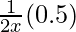
= 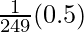
= 0.5/14
= 0.0357
Hence, the approximate value of √49.5 = 7 + 0.0357 = 7.0357
(iii) √0.6
We take y = √x
Let x = 0.64 and △x = -0.04
△y = √(x +△x) – √x
= √0.6 – √0.64
= √0.6 – 0.8
or √0.6 = 0.8 + △y
Here, dy is approximately equal to △y
dy = (dy/dx)△x
= 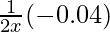
= 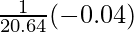
= -0.04/1.6
= -0.025
Hence, the approximate value of √0.6 = 0.8 – 0.025 = 0.775
(iv) (0.009)1/3
We take y = x1/3
Let x = 0.008 and △x = 0.001
△y = (x +△x)1/3 – x1/3
= (0.009)1/3 – (0.008)1/3
= (0.009)1/3 – 0.2
or (0.009)1/3 = 0.2 + △y
Here, dy is approximately equal to △y
dy = (dy/dx)△x
= 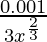
= 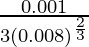
= 0.0083
Hence, the approximate value of (0.009)1/3 = 0.2 + 0.0083 = 0.2083
(v) (0.999)1/10
We take y = x1/10
Let x = 1 and △x = -0.001
△y = (x +△x)1/10 – x1/10
= (1)1/10 – (0.001)1/10
= (1)1/10 – 1
or (1)1/10 = 1 + △y
Here, dy is approximately equal to △y
dy = (dy/dx)△x
= 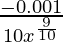
= 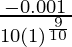
= -0.0001
Hence, the approximate value of (0.999)1/10 = 1 – 0.0001 = 0.9999
(vi) (15)1/4
We take y = x1/4
Let x = 16 and △x = -1
△y = (x +△x)1/4 – x1/4
= (15)1/4 – (16)1/4
= (15)1/4 – 2
or (15)1/4 = 2 + △y
Here, dy is approximately equal to △y
dy = (dy/dx)△x
= 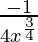
= 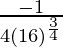
= -1/32
Hence, the approximate value of (15)1/4 = 2 – 1/32 = 1.9687
(vii) (26)1/3
We take y = x1/3
Let x = 27 and △x = -1
△y = (x +△x)1/3 – x1/3
= (26)1/3 – (27)1/3
= (26)1/3 – 3
or (26)1/3 = 3 + △y
Here, dy is approximately equal to △y
dy = (dy/dx)△x
= 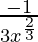
= 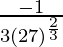
= -1/27
Hence, the approximate value of (26)1/3 = 3 – 1/27 = 2.962
(viii) (255)1/4
We take y = x1/4
Let x = 256 and △x = -1
△y = (x +△x)1/4 – x1/4
= (255)1/4 – (256)1/4
= (255)1/4 – 4
or (255)1/4 = 4 + △y
Here, dy is approximately equal to △y
dy = (dy/dx)△x
= 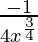
= 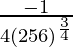
= -1/256
Hence, the approximate value of (255)1/4 = 4 – 1/256 = 3.996
(ix) (82)1/4
We take y = x1/4
Let x = 81 and △x = 1
△y = (x +△x)1/4 – x1/4
= (82)1/4 – (81)1/4
= (82)1/4 – 3
or (82)1/4 = 3 + △y
Here, dy is approximately equal to △y
dy = (dy/dx)△x
= 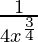
= 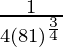
= 1/108
Hence, the approximate value of (82)1/4 = 3 + 1/108 = 3.009
(x) (401)1/2
We take y = x1/2
Let x = 400 and △x = 1
△y = (x +△x)1/2 – x1/2
= (401)1/2 – (400)1/2
= (401)1/2 – 20
or (401)1/2 = 20 + △y
Here, dy is approximately equal to △y
dy = (dy/dx)△x
= 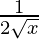
= 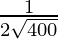
= 1/40
Hence, the approximate value of (401)1/2 = 20 + 1/40 = 20.025
(xi) (0.0037)1/2
We take y = x1/2
Let x = 0.0036 and △x = 0.0001
△y = (x +△x)1/2 – x1/2
= (0.0037)1/2 – (0.0036)1/2
= (0.0037)1/2 – 0.06
or (0.0037)1/2 = 0.06 + △y
Here, dy is approximately equal to △y
dy = (dy/dx)△x
= 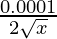
= 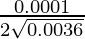
= 0.0001/0.12
Hence, the approximate value of (0.0037)1/2 = 0.06 + 0.0001/0.12 = 0.0608
(xii) (26.57)1/3
We take y = x1/3
Let x = 27 and △x = -0.43
△y = (x +△x)1/3 – x1/3
= (26.57)1/3 – (27)1/3
= (26.57)1/3 – 3
or (26.57)1/3 = 3 + △y
Here, dy is approximately equal to △y
dy = (dy/dx)△x
= 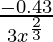
= 
= -0.43/27
Hence, the approximate value of (26.57)1/3 = 3 – 0.43/27 = 2.984
(xiii) (81.5)1/4
We take y = x1/4
Let x = 81 and △x = 0.5
△y = (x +△x)1/4 – x1/4
= (81.5)1/4 – (81)1/4
= (81.5)1/4 – 3
or (81.5)1/4 = 3 + △y
Here, dy is approximately equal to △y
dy = (dy/dx)△x
= 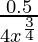
= 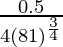
= 0.5/108
Hence, the approximate value of (81.5)1/4 = 3 + 0.5/108 = 3.004
(xiv) (3.968)3/2
We take y = x3/2
Let x = 4 and △x = -0.032
△y = (x +△x)3/2 – x3/2
= (3.968)3/2 – (4)3/2
= (3.968)3/2 – 8
or (3.968)3/2 = 8 + △y
Here, dy is approximately equal to △y
dy = (dy/dx)△x
= 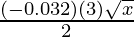
= 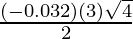
= -0.096
Hence, the approximate value of (3.968)3/2 = 8 – 0.096 = 7.904
(xv) (32.15)1/5
We take y = x1/5
Let x = 32 and △x = 0.15
△y = (x +△x)1/5 – x1/5
= (32.15)1/5 – (32)1/5
= (32.15)1/5 – 2
or (32.15)1/5 = 2 + △y
Here, dy is approximately equal to △y
dy = (dy/dx)△x
= 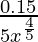
= 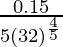
= 0.15/80
Hence, the approximate value of (32.15)1/5 = 2 + 0.15/80 = 2.0018
Question 2. Find the approximate value of f(2.01), where f(x) = 4x2 + 5x + 2.
Solution:
Find the approximate value of f(2.01)
So, f(2.01) = f(2 + 0.01)
x = 2 and △x = 0.01
Given that f(x) = y = 4x2 + 5x + 2 -(1)
On differentiating we get
dy/dx = 8x + 5
dy = (8x + 5)dx = (8x + 5)△x
Now changing x = x + Δx and y = y +Δy in eq(1)
f(x + Δx) = y + Δy
f(2.01) = y + Δy -(2)
f(2 + .01) = y + Δy
since
then Δy = dy and Δx = dx
From eq(2), we get
f(2.01) = (4x2 + 5x + 2) + (8x + 5)△x
= (4(2)2 + 5(2) + 2) + (8(2) + 5)(0.01)
= 16 + 10 + 2 + 0.16 + 0.05
= 28.21
Question 3. Find the approximate value of f(5.001), where f(x) = x3 – 7x2 + 15.
Solution:
Find the approximate value of f(5.001)
So, f(5.001) = f(5 + .001)
x = 5 and △x = 0.01,
Given that f(x) = y = x3 – 7x2 + 15 -(1)
On differentiating we get
dy/dx = 3x2 – 14x
dy = (3x2 – 14x) dx = (3x2 – 14x) △x
Now changing x = x + Δx and y = y +Δy in eq(1)
f(x + Δx) = y + Δy
f(5.001) = y + Δy -(2)
f(5 + .001) = y + Δy
since
then Δy = dy and Δx = dx
From eq(2), we get
f(5.001) = (x3 – 7x2 + 15) + (3x2 – 14x) △x
= ((5)3 – 7(5)2 + 15) + (3(5)2 – 14(5)) (0.001)
= 125 – 175 + 15 + 0.075 + 0.07
= -34.995
Question 4. Find the approximate change in the volume of a cube of side x meters caused by increasing the side by 1%.
Solution:
Volume of cube = x3
V = x3
On differentiating we get
dV/dx = 3x2
Given that Δx = 0.0
dV = 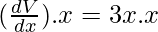
dV = (3x2)(-0.01x)
= 0.03x3m3
Thus, the approximate change in volume is 0.03x3m3
Question 5.Find the approximate change in the surface area of a cube of side x meters caused by decreasing the side by 1%.
Solution:
Surface area of cube = 6x2
S = 6x2
On differentiating we get
dS/dx = 12x
Given that Δx = -0.01[-ve sign because of decrease]
dS = 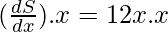
dS = (12x)(-0.01x)
= -0.12x2m2
Thus, the approximate change in volume is -0.12x2m2
Question 6. If the radius of a sphere is measured as 7m with an error of 0.02m, then find the approximate error in calculating its value.
Solution:
Let r be the radius of the sphere and △r be the error in measuring the radius,
then r = 7m and △r = 0.02m.
Now the volume V of the sphere is given by,
v = 4/3πr2
On differentiating we get
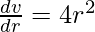
Therefore, dv = (4πr2)Δr = 4π(7)2.(0.02)
= 12.30m3
Thus, the approximate error in calculating the volume is 12.30m3
Question 7. If the radius of a sphere is measured as 9m with an error of 0.03m, then find the approximate error in calculating its surface area.
Solution:
Let r be the radius of the sphere and Δr be the error in measuring the radius.
Then r = 9m and Δr = 0.03m.
Now the surface area S of the sphere is given by,
S = 4πr2
On differentiating we get
dS/dr = 8πr
Therefore, dS = (8πr)Δr
= 8π(9).(0.03)
= 2.16πm2
Thus, the approximate error in measuring the surface area is 2.16πm2.
Question 8. If f(x) = 3x2 + 15x + 5, then the approximate value of f(3.02) is
(A) 47.66 (B) 57.66 (C)67.66 (D)77.66
Solution:
Given: f(x) = y = 3x2 + 15x + 5 -(1)
f(3.02) = f(3 + 0.2)
So, x = 3 and Δx = 0.02
On differentiating eq(1) we get
f'(x) = y = 6x + 15
dy = (6x + 15) dx = (6x + 15)Δx
Now changing x = x + Δx and y = y +Δy in eq(1)
f(x + Δx) = y + Δy
f(3.02) = y + Δy -(2)
f(3 + 0.2) = y + Δy
since
then Δy = dy and Δx = dx
From eq(2), we get
f(3.02) = (3x2 + 15x + 5) + (6x + 15)Δx
f(3.02) = (3x2 + 15x + 5) + (6x + 15)(0.02)
= (3(3)2 + 15(3) + 5) + (6(3)+ 15)(0.02)
= 27 + 45 + 5 + 0.36 + 0.3
= 77.66
Hence the correct option is 77.66
Question 9. The approximate change in the volume of a cube of side x meters caused by increasing the side by 3% is
(A) 0.06x3 m3 (B) 0.6x3 m3 (C)0.09x3 m3 (D)0.9x3 m3
Solution:
We have
Volume of cube = v = x3
On differentiating we get
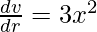
Given that the side increasing 3%, so Δx = 0.03x
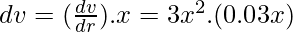
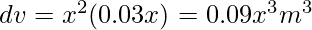
Thus, the approximate change is 0.09x3m3
The correct option is (C)
Share your thoughts in the comments
Please Login to comment...