Differentiate w.r.t x the function in Exercise 1 to 11.
Question 1. (3 x2 – 9x – 5)9
Solution:
Let us assume y = (3x2 – 9x – 5)9
Now, differentiate w.r.t x
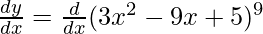
Using chain rule, we get
= 9(3x2 – 9 x + 5)8 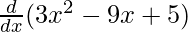
= 9(3x2 – 9x + 5)8.(6x – 9)
= 9(3x 2 – 9x + 5)8.3(2x – 3)
= 27(3x2 – 9x + 5)8 (2x – 3)
Question 2. sin3 x + cos6 x
Solution:
Let us assume y = sin3 x + cos6 x
Now, differentiate w.r.t x
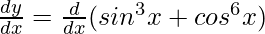
Using chain rule, we get
= 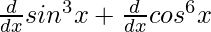
= 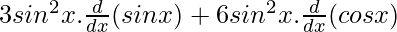
= 3 sin2 x. cos x + 6 cos5 x.(-sin x)
= 3 sin x cos x(sin x – 2 cos4 x)
Question 3. 5x3 cos 2 x
Solution:
Let us assume y = 5x3 cos 2x
Now we’re taking logarithm on both the sides
logy = 3 cos 2 x log 5 x
Now, differentiate w.r.t x
![Rendered by QuickLaTeX.com \frac{1}{y}\frac{dy}{dx}=3[log5x.\frac{d}{dx}(cos2x)+cos2x.\frac{d}{dx}(log5x)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d0b1b49987b74a00fdd932a7c5b90fae_l3.png)
![Rendered by QuickLaTeX.com \frac{dy}{dx}=3y[log 5x(-sin2x).\frac{d}{dx}(2x)+cos2x.\frac{1}{5x}.\frac{d}{dx}(5x)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8b50c2359a134eed61976518919b3fe1_l3.png)
![Rendered by QuickLaTeX.com \frac{dy}{dx}=3y[-2sin2xlog5x+\frac{cos2x}{x}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4b45f61ffee5452e4e07c6be07d075f7_l3.png)
![Rendered by QuickLaTeX.com \frac{dy}{dx}=3y[\frac{3cos2x}{x}-6sin2xlog5x]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cc49eccaef4e885f0553ada3faefd40a_l3.png)
![Rendered by QuickLaTeX.com \frac{dy}{dx}=5x^{3cos2x}[\frac{3cos2x}{x}-6sin2xlog5x]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e6fb17e03878bac7c8956ac577442360_l3.png)
Question 4. sin-1(x√x), 0 ≤ x ≤ 1
Solution:
Let us assume y = sin-1(x√x)
Now, differentiate w.r.t x
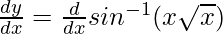
Using chain rule, we get
=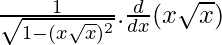
=![Rendered by QuickLaTeX.com \frac{1}{\sqrt{1-x^3}}.\frac{d}{dx}[x^{\frac{3}{2}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-04a33182ece23bae50e8cea8b4dd732e_l3.png)
=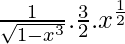
=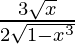
=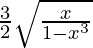
Question 5. 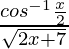 ,-2 < x < 2
,-2 < x < 2
Solution:
Let us assume y =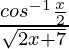
Now, differentiate w.r.t x and by quotient rule, we obtain
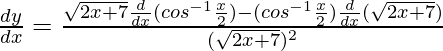
= ![Rendered by QuickLaTeX.com \frac{\sqrt{2x+7}[\frac{-1}{\sqrt{1-(\frac{x}{2})^2}}.\frac{d}{dx}(\frac{x}{2})]-(cos^{-1}\frac{x}{2})\frac{1}{2\sqrt{2x+7}}.\frac{d}{dx}(2x+7)}{2x+\frac{7}{2}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-928ac7ece6a1ec001eba42741795774e_l3.png)
= ![Rendered by QuickLaTeX.com \frac{\sqrt{2x+7}\frac{-1}{\sqrt{4-x^2}}-[cos^{-1}\frac{x}{2}]\frac{2}{2\sqrt{2x+7}}}{2x+7}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5482b8d0de56fb7d74a6c4bd5e28cc2f_l3.png)
= 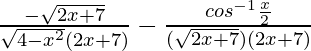
= ![Rendered by QuickLaTeX.com -[\frac{1}{\sqrt{4-x^2}\sqrt{2x+7}}+\frac{cos^{-1}\frac{x}{2}}{(2x+7)^\frac{1}{2}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ff2ddba68516f46c431046b166484041_l3.png)
Question 6. 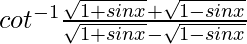 , 0 < x < π/2
, 0 < x < π/2
Solution:
Let us assume y = 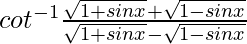 ……(1)
……(1)
Now solve 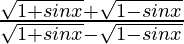
= 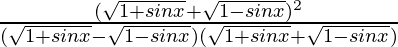
= 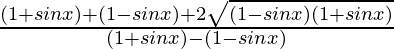
= 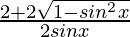
= 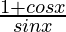
= 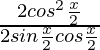
= cotx/2
Now put this value in eq(1), we get
y = cot-1(cotx/2)
y = x/2
Now, differentiate w.r.t x
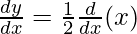
dy/dx = 1/2
Question 7. (log x) log x, x > 1
Solution:
Let us assume y = (log x)log x
Now we are taking logarithm on both sides,
log y = log x .log(log x)
Now, differentiate w.r.t x on both side, we get
![Rendered by QuickLaTeX.com \frac{1}{y}\frac{dy}{dx}=\frac{d}{dx}[logx.log(logx)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c071ddef9397e29a3d62df12b0d7df3e_l3.png)
![Rendered by QuickLaTeX.com \frac{1}{y}\frac{dy}{dx}=log(logx).\frac{d}{dx}(log x)+logx.\frac{d}{dx}[log(logx)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9cd6e27615e47b64fe0083e9b7841cf2_l3.png)
![Rendered by QuickLaTeX.com \frac{dy}{dx}=y[log(logx).\frac{1}{x}+logx.\frac{1}{logx}.\frac{d}{dx}(logx)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2ac351d05256278d9a3c4f690bb32378_l3.png)
![Rendered by QuickLaTeX.com \frac{dy}{dx}=y[\frac{1}{x}log(logx)+\frac{1}{x}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-78f339f25197d6358717a80fd20a7da7_l3.png)
![Rendered by QuickLaTeX.com \frac{dy}{dx}=(logx)^{logx}[\frac{1}{x}+\frac{log(logx)}{x}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-aac4d3eb201d904138fff97287b79354_l3.png)
Question 8. cos(a cos x + b sin x), for some constant a and b.
Solution:
Let us assume y = cos(a cos x + b sin x)
Now, differentiate w.r.t x
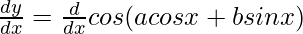
By using chain rule, we get
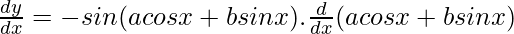
= -sin x(a cos x + b sin x).[a (-sin x) + b cos x]
= (a sin x – b cos x).sin (a cos x + b sin x)
Question 9. (sin x – cos x) (sin x – cos x), π/4 < x < 3π/4
Solution:
Let us assume y = (sin x – cos x)(sin x – cos x)
Now we are taking logarithm on both sides,
log y = (sin x – cos x).log(sin x – cos x)
Now, differentiate w.r.t x, we get
![Rendered by QuickLaTeX.com \frac{1}{y}\frac{dy}{dx}=\frac{d}{dx}[(sinx-cosx)log(sinx-cosx)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-48129dcfde816946dd0aede0363f226b_l3.png)
Using chain rule, we get
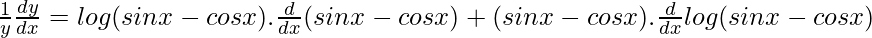
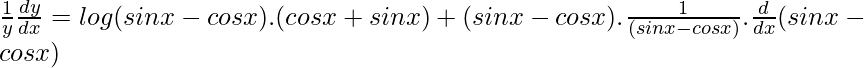
dy/dx = (sinx – cosx)(sinx – cosx)[(cosx + sinx).log(sinx – cosx) + (cosx + sinx)]
dy/dx = (sinx – cosx)(sinx – cosx)(cosx + sinx)[1 + log (sinx – cosx)]
Question 10. xx + x a + a x + aa for some fixed a > 0 and x > 0
Solution:
Let us assume y = xx + xa + ax + aa
Also, let us assume xx = u, xa = v, ax = w, aa = s
Therefore, y = u + v + w + s
So, on differentiating w.r.t x, we get
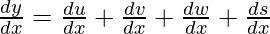 ……….(1)
……….(1)
So first we solve: u = xx
Now we are taking logarithm on both sides,
log u = log xx
log u = x log x
On differentiating both sides w.r.t x, we get
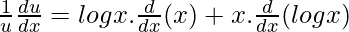
![Rendered by QuickLaTeX.com \frac{du}{dx}=u[logx.1+x.\frac{1}{x}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d15f597f14b4a24481baccf3f04e5837_l3.png)
du/dx = xx[logx + 1] = xx(1 + logx) …….(2)
Now we solve: v = xa
On differentiating both sides w.r.t x, we get
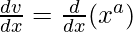
dv/dx = ax(a – 1) ……(3)
Now we solve: w = ax
Now we are taking logarithm on both sides,
log w =log a x
log w = x log a
On differentiating both sides w.r.t x, we get
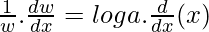
dw/dx = w loga
dw/dx = axloga ………(4)
Now we solve: s = a a
So, on differentiating w.r.t x, we get
ds/dx = 0 ………(5)
Now put all these values from eq(2), (3), (4), (5) in eq(1), we get
dy/dx = xx(1 + logx) + ax(a – 1) + axloga + 0
= xx (1 + log x) + axa -1 + ax log a
Question 11. Differentiate w.r.t x, 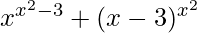 , for x > 3
, for x > 3
Solution:
Let us assume y =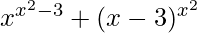
Also let us considered u = 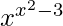 and v =
and v = 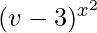
so, y = u + v
On differentiating both side w.r.t x, we get
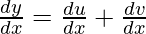 …….(1)
…….(1)
So, now we solve, u = 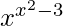
Now we are taking logarithm on both sides,
log u = log 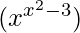
log u = (x 2 – 3) log x
On differentiating w.r.t x, we get
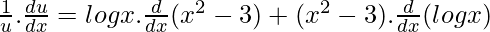
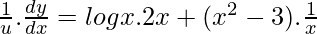
=![Rendered by QuickLaTeX.com \frac{du}{dx}= x^{x^2-3}.[\frac{x^2-3}{x}+ 2xlogx]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f6504fbbedf86e5f7a77961233eacf1d_l3.png) …….(2)
…….(2)
Now we solve: v = 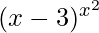
Now we are taking logarithm on both sides,
log v = 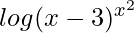
log v = x2 log(x – 3)
On differentiating both sides w.r.t x, we get
![Rendered by QuickLaTeX.com \frac{1}{v}.\frac{dv}{dx}= log (x-3).\frac{d}{dx}(x^2)+x^2\frac{d}{dx}[log(x-3)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ee6c1c3363213b70998c532470f5fe61_l3.png)
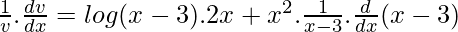
![Rendered by QuickLaTeX.com \frac{dv}{dx}=v[2xlog(x-3)+\frac{x^2}{x-3}.1]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-185778d96dbc98c420fc0fe03849bbb2_l3.png)
![Rendered by QuickLaTeX.com \frac{dv}{dx}=(x-3)^{x^2}[\frac{x^2}{x-3}+2xlog(x-3)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-400addd6546a52ea3f5948415068a70a_l3.png) …..(3)
…..(3)
Now put all these values from eq(2), and (3) in eq(1), we get
![Rendered by QuickLaTeX.com \frac{dy}{dx}= x^{x^2-3}[\frac{x^2-3}{x}+2xlogx]+(x-3)^{x^2}[\frac{x^2}{x-3}+2xlog(x-3)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5a550e01c895030ed21a9eda168b9ccb_l3.png)
Question 12. Find dy/dx , if y = 12(1 – cos t), x = 10 (t – sin t), -π/2 < t < π/2
Solution:
According to the question
y = 12(1 – cos t) ……(1)
x = 10 (t – sin t) ……(2)
So, \frac{dy}{dx}= \frac{\frac{dy}{dt}}{\frac{dx}{dt}} ……(3)
On differentiating eq(1) w.r.t t, we get
![Rendered by QuickLaTeX.com \frac{dy}{dt} = \frac{d}{dt} [12 (1 - cost)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9ded82de7bbd4396c457999d2ac6ccdf_l3.png)
= 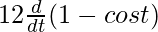
= 12.[0 – (- sin t)]
= 12 sin t
On differentiating eq(2) w.r.t t, we get
![Rendered by QuickLaTeX.com \frac{dx}{dt}=\frac{d}{dt}[10. (t - sin t)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a8fc9a390561b4777c023ccf46cef5b0_l3.png)
= 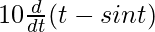
= 10(1 – cos t)
Now put the value of dy/dt and dx/dt in eq(3), we get
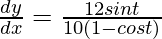
= 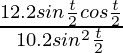
= 6/5 cot t/2
Question 13. Find dy/dx, if y = sin-1 x + sin-1√1-x2, 0 < x < 1
Solution:
According to the question
y = sin-1 x + sin-1√1 – x2
On differentiating w.r.t x, we get
![Rendered by QuickLaTeX.com \frac{dy}{dx}=\frac{d}{dx}[sin^{-1}x+sin ^{-1}\sqrt{1-x^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e516f5e48bb584921a1e8ca01aac2d91_l3.png)
Using chain rule, we get
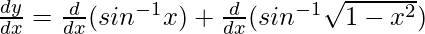
= 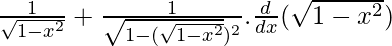
= 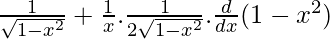
= 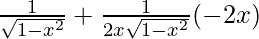
= 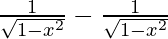
dy/dx = 0
Question 14. If x√1 + y + y√1 + x = 0, for, -1 < x < 1, prove that 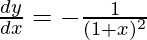
Solution:
According to the question
x√1 + y = -y√1 + x
On squaring both sides, we get
x2 (1 + y) = y2 (1 + x)
⇒ x2 + x2 y = y2 + x y2
⇒ x2 – y2 = xy 2 – x2 y
⇒ x2 – y2 = xy (y – x)
⇒ (x + y)(x – y) = xy (y – x)
⇒ x + y = -xy
⇒ (1 + x) y = -x
⇒ y = -x/(1 + x)
On differentiating both sides w.r.t x, we get
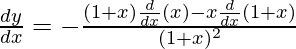
= 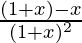
= 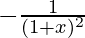
Hence proved.
Question 15. If (x – a)2 + (y – b)2 = c 2, for some c > 0, prove that ![Rendered by QuickLaTeX.com \frac{[1+(\frac{dy}{dx})^2]^\frac{3}{2}} {\frac{d^2y}{dx^2}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-332cb28f2a10cef087f8c053cab15b63_l3.png) is a constant independent of a and b.
is a constant independent of a and b.
Solution:
According to the question
(x – a)2+ (y – b)2= c2
On differentiating both side w.r.t x, we get
![Rendered by QuickLaTeX.com \frac{d}{dx}[(x-a)^2]+\frac{d}{dx}[(y-b)^2]=\frac{d}{dx}(c^2)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a65a76df92b31929bc96271f926665b4_l3.png)
⇒ 2(x – a).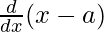 + 2(y – b)
+ 2(y – b)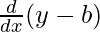 = 0
= 0
⇒ 2(x – a).1 + 2(y – b).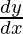 = 0
= 0
⇒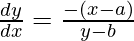 …….(1)
…….(1)
Again on differentiating both side w.r.t x, we get
![Rendered by QuickLaTeX.com \frac{d^2y}{dx^2} = \frac{d}{dx}[\frac{-(x-a)}{y-b}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-138f0e2be90874b839599ccfab6ca87f_l3.png)
![Rendered by QuickLaTeX.com = -[\frac{(y-b).\frac{d}{dx}(x-a)-(x-a).\frac{d}{dx}(y-b)}{(y-b)^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-596cba4b87c610c93481364ae8041fb8_l3.png)
![Rendered by QuickLaTeX.com =-[\frac{(y-b)-(x-a).\frac{dy}{dx}}{(y-b)^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-55457f6e8f9b90f73a06e8b7ab021d13_l3.png)
![Rendered by QuickLaTeX.com = -[\frac{(y-b)-(x-a).\{-\frac{(x-a)}{y-b}\}}{(y-b)^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-72c473b7cc677890e3cad86f1f2963b2_l3.png) …….[From equation (1)]
…….[From equation (1)]
![Rendered by QuickLaTeX.com =-[\frac{(y-b)^2+(x-a)^2}{(y-b)^3}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4a46e8809c5ee1e7d0d89a97f50a5d90_l3.png)
![Rendered by QuickLaTeX.com [\frac{1+[\frac{dy}{dx}]^2}{\frac{d^2y}{dx^2}}]^{\frac{3}{2}}= \frac{[1+\frac{(x-a)^2}{(y-b)^2}]^{\frac{3}{2}}}{-[\frac{(y-b)^2 + (x-a)^2}{(y-b)^3}]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-018d25e7407f1a0978d4fe72befce076_l3.png)
=![Rendered by QuickLaTeX.com \frac{[\frac{[(y-b)^2+(x-a)^2]}{(y-b)^2}]^{\frac{3}{2}}}{-[\frac{(y-b)^2+(x-a)^2}{(y-b)^3}]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-47c73e07695be04410c04dacb47abe07_l3.png)
=![Rendered by QuickLaTeX.com \frac{[\frac{c^2}{(y-b)^2}]\frac{3}{2}}{-\frac{c^2}{(y-b)^3}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-52915b2ff0ab706529a3c46883284d7b_l3.png)
=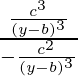
= – c, which is constant and is independent of a and b.
Hence proved.
Question 16. If cos y = x cos (a + y), with cos a ≠ ±1, prove that 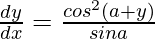
Solution:
According to the question
cos y = x cos (a + y)
On differentiating both side w.r.t x, we get
![Rendered by QuickLaTeX.com \frac{d}{dx}[cos y]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-18f32f80896406f9b3b800837bb65444_l3.png) =
= ![Rendered by QuickLaTeX.com \frac{d}{dx}[x cos(a + y)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-12daf24fe228c934b29b610860b9ce3c_l3.png)
⇒ – sin y dy/dx = cos (a + y). 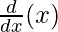 + x
+ x![Rendered by QuickLaTeX.com \frac{d}{dx}[cos (x+y)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-20bad57f0d3235b66d516530c0c9ffcb_l3.png)
⇒ – sin y dy/dx = cos (a + y) + x [-sin (a + y)]dy/dx
⇒ [x sin (a + y) – sin y] dy/dx = cos (a + y) ……..(1)
Since cos y = x cos (a + y), x =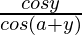
Now we can reduce eq(1)
![Rendered by QuickLaTeX.com [\frac{cosy}{cos(a+y)}.sin(a+y)-siny]\frac{dy}{dx}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f097e2a37e4def8828d80e5c3529ff98_l3.png) = cos(a + y)
= cos(a + y)
⇒ [cos y.sin (a + y)- sin y.cos (a + y)].dy/dx = cos2(a + y)
⇒ sin(a + y – y)dy/dx = cos2(a + b)
⇒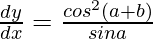
Hence proved.
Question 17. If x = a (cos t + t sin t) and y = a (sin t – t cos t), find 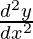
Solution:
According to the question
x = a (cos t + t sin t) …..(1)
y = a (sin t – t cos t) …..(2)
So, \frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}} …..(3)
On differentiating eq(1) w.r.t t, we get
dx/dt = a. 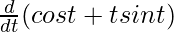
Using chain rule, we get
= a[-sin t +sin t. 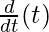 + t.
+ t.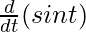 ]
]
= a [-sin t + sin t + t cos t]
= at cos t
On differentiating eq(2) w.r.t t, we get
dy/dt = a. 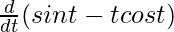
Using chain rule, we get
= a [cos t – [cost.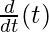 + t.
+ t.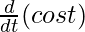 ]]
]]
= a[cos t – {cos t – t sin t}]
= at sin t
Now put the values of dx/dt and dy/dt in eq(1), we get
dy/dx = at sin t/at cos t = tan t
Again differentiating both side w.r.t x, we get
![Rendered by QuickLaTeX.com \frac{d^2y}{dx^2}= \frac{d}{dx}[\frac{dy}{dx}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d531939e0958fb3068a452d4e2d8a1e7_l3.png)
= 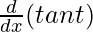
= sec 2 t.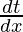
= sec2 t.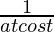 ……..[dx/dt = atcost ⇒ dt/dx = 1/atcost]
……..[dx/dt = atcost ⇒ dt/dx = 1/atcost]
= sec3t/at
Question 18. If f(x) = |x|3, show that f”(x) exists for all real x and find it.
Solution:
As we know that |x| = 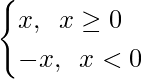
So, when x ≥ 0, f(x) = |x|3 = x3
So, on differentiating both side w.r.t x, we get
f'(x) = 3x2
Again, differentiating both side w.r.t x, we get
f”(x) = 6 x
When x < 0, f(x) = |x|3 = -x3
So, on differentiating both side w.r.t x, we get
f'(x) = – 3x2
Again, differentiating both side w.r.t x, we get
f”(x) = -6 x
So, for f(x) = |x|3, f”(x) exists for all real x, and is given by
f”(x) = 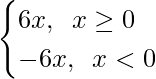
Question 19. Using mathematical induction prove that 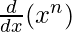 = (nx)n – 1 for all positive integers n.
= (nx)n – 1 for all positive integers n.
Solution:
So, P(n) = 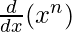 = (nx)n – 1
= (nx)n – 1
For n = 1:
P(1) : 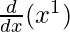 = (1x)1 – 1 =1
= (1x)1 – 1 =1
Hence, P(n) is true for n = 1
Let us considered P(k) is true for some positive integer k.
So, P(k): 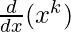 = (kx)k – 1
= (kx)k – 1
For P(k + 1): 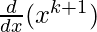 = ((k + 1)x)(k + 1) – 1
= ((k + 1)x)(k + 1) – 1
x k 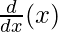 + x.
+ x.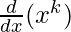 ….(Using applying product rule)
….(Using applying product rule)
= x k .1 + x . k . x k-1
= x k + k x k
= (k + 1) x k
= (k + 1) x(k + 1) – 1
Hence, P(k+1) is true whenever P(k) is true.
So, according to the principle of mathematical induction, P(n) is true for every positive integer n.
Hence proved.
Question 20. Using the fact that sin(A + B) = sin A cos B + cos A sin B and the differentiation, obtain the sum formula for cosines.
Solution:
According to the question
sin(A + B) = sin A cos B + cos A sin B
On differentiating both sides w.r.t x, we get
![Rendered by QuickLaTeX.com \frac{d}{dx} [sin(A+B)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-be53ffc306e7efadc4b2bfde000a543d_l3.png) =
= 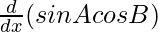 +
+ 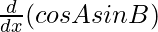
⇒ cos (A + B).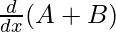 = cos B.
= cos B. 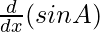 + sin A.
+ sin A. 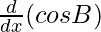 + sin B.
+ sin B.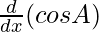 + cos A.
+ cos A. 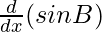
⇒ cos (A+B).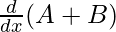 = cos B.cos A
= cos B.cos A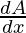 + sin A (-sin B)
+ sin A (-sin B) 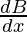 + sin B (-sin A).
+ sin B (-sin A).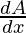 + cos A cos B
+ cos A cos B 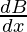
⇒ cos (A + B).![Rendered by QuickLaTeX.com [ \frac{dA}{dx}+ \frac{dB}{dx}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-18523a1ac535df04a3abdf6969c34f71_l3.png) =(cos A cos B – sin A sin B).
=(cos A cos B – sin A sin B). ![Rendered by QuickLaTeX.com [ \frac{dA}{dx}+ \frac{dB}{dx}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-20d883d840722fda1f0ee170310a8b08_l3.png)
Hence, cos (A + B) = cos A cos B – sin A sin B
Question 21. Does there exist a function which is continuous everywhere but not differentiable to exactly two points? Justify your answer.
Solution:
Let us consider a function f given as
f(x) = |x – 1| + |x – 2|
As we already know that the modulus functions are continuous at every point
So, there sum is also continuous at every point but not differentiable at every point x = 0
Let x = 1, 2
Now at x = 1
L.H.D = lim x⇢ 1– 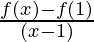
L.H.D = limh⇢0 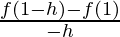
= limh⇢0 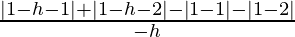
= limh⇢0 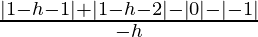
= limh⇢0 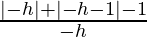
= limh⇢0 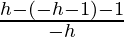
= limh⇢0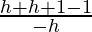
= limh⇢0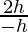
= -2
R.H.D = limx⇢1+ 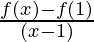
R.H.D = limh⇢0 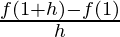
= limh⇢0 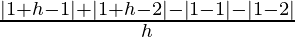
= limh⇢0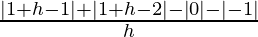
= limh⇢0 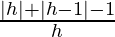
= limh⇢0 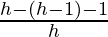
= limh⇢0 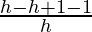
= limh⇢0 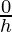
= 0
Since L.H.D ≠ R.H.D
So given function f is not differentiable at x = 1.
Similarly, we get that the given function is not differentiable at x = 2.
Hence, there exist a function which is continuous everywhere but not differentiable to exactly two points.
Question 22. If 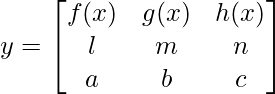 ,prove that
,prove that 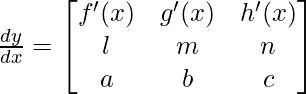
Solution:
Given that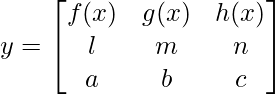
⇒ y =(mc – nb) f(x)- (lc – na )g(x) +(lb – ma) h(x)
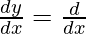 [(mc -nb) f(x)] –
[(mc -nb) f(x)] – 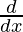 [(lc – na) g(x)] +
[(lc – na) g(x)] + 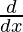 [(lb – ma) h(x)]
[(lb – ma) h(x)]
= (mc – nb) f'(x) – (lc – na) g'(x) + (lb – ma ) h’ (x)
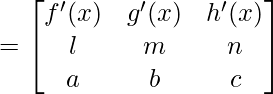
So,
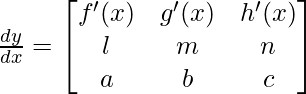
Hence proved.
Question 23. If y = 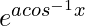 ,-1 ≤ x ≤ 1, show that
,-1 ≤ x ≤ 1, show that 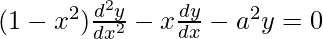
Solution:
According to the question
y = 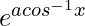
Now we are taking logarithm on both sides,
log y = a cos-1 x log e
log y = a cos -1 x
On differentiating both sides w.r.t x, we get
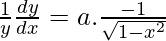
⇒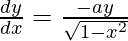
On squaring both sides,we get
![Rendered by QuickLaTeX.com [\frac{dy}{dx}]^2=\frac{a^2y^2}{1-x^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4644f5fe41156317371c3e3f92d4f147_l3.png)
⇒(1-x 2)![Rendered by QuickLaTeX.com [\frac{dy}{dx}]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-67d3ea79fa3cfe84e8d0feb1fd2de116_l3.png) =a 2 y 2
=a 2 y 2
On differentiating again both the side w.r.t x, we get
![Rendered by QuickLaTeX.com [\frac{dy}{dx}]^2 \frac{d}{dx}(1-x^2)+(1-x^2)\frac{d}{dx} [[\frac{dy}{dx}]^2]=a^2 \frac{d}{dx}(y^2)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d132900d3817d646cbb1515643249152_l3.png)
⇒![Rendered by QuickLaTeX.com [\frac{dy}{dx}]^2(-2x)+(1-x^2).2 \frac{dy}{dx}. \frac{d^2y}{dx^2}=a^2.2y \frac{dy}{dx}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1cd1e041a6ebeb93a8e67d43c33b104b_l3.png)
⇒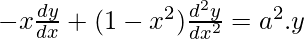
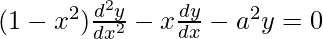
Hence proved
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...