Content of this article has been merged with Chapter 6 Application of Derivatives -Exercise 6.3 as per the revised syllabus of NCERT.
Question 14. Find the equations of the tangent and normal to the given curves at the indicated points:
(i) y = x4– 6x3 + 13x2 – 10x+ 5 at (0, 5)
(ii) y = x4 – 6x3 + 13x2 – 10x + 5 at (1, 3)
(iii) y = x3 at(1, 1)
(iv) y = x2 at(0, 0)
(v) x = cos t, y = sin t at t = π/4
Solution:
(i) Given curve
y = x4 – 6x3 + 13x2 – 10x + 5
Given point, (0, 5)
dy/dx = 4x3 – 18x2 + 26x – 10
dy/dx = 4(0)3 – 18(0)2 + 26(0) – 10
dy/dx = -10,
-dx/dy = 1/10
Now, with the help of points slope form
y – y1 = m(x – x1)
y – 5 = -10(x – 0)
y + 10x = 5 is the required equation of the tangent
For equation of normal,
y – y1 = 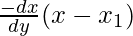
y – 5 = 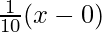
10y – x – 50 is the equation of normal.
(ii) Given curve: y = x4 – 6x3 + 13x2 – 10x + 5
Given point is (1, 3)
dy/dx = 4x3 – 18x2 + 26x – 10
dy/dx = 4(1)3 – 18(1)2 + 26(1) – 10
dy/dx = 4 – 18 + 26 – 10 = 2
dy/dx = 2
-dx/dy = -1/2
Using point slope form, equation of tangent is
y – y1 = dy/dx(x – x1)
y – 3 = 2(x – 1)
y – 2x = 1 is the equation of tangent.
Using point slope form, equation of normal is
y – y1 = -dx/dy(x – 1)
y – 3 = -1/2(x – 1)
2y – 6 = -x + 1
2y + x = 7 is the equation of normal.
(iii) Given curve : y = x3
Given point is (1, 1)
dy/dx = 3x2
dy/dx = 3(1)2 = 3
dy/dx = 3 & -dx/dy = -1/3
Using point slope form, equation of tangent is y – y1 = dy/dx(x – x1)
y – y1 = dy/dx(x – x1)
y – 1 = 3(x – 1)
y – 3x + 2 = 0 is the equation of tangent
Using point slope form, equation of normal is
y – y1 = 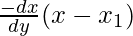
y – 1 = 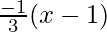
3y – 3 = -x + 1
3y + x = 4 is the equation of normal.
(iv) Given curve: y = x2
Given point (0, 0)
dy/dx = 2x
dy/dx = 0
dy/dx = 0 & -dx/dy = not defined is
y – y1 = dy/dx(x – x1)
y – 0 = 0(x – 0)
y = 0 is the equation of tangent.
Using point slope form, equation of normal is
y – y1 = 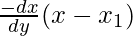 -(1)
-(1)
-dx\dy is undefined, so we can write eq(1) as
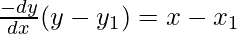
Now putting dy/dx = 0 we get
0(y – 0) = x-0
x = 0 is the equation of normal.
(v) Equation of curve: x = cos t and y = sin t
Point t = π/4
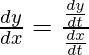 -(1)
-(1)
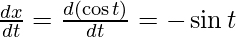
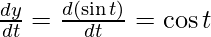
On putting these values in eq(1), we get
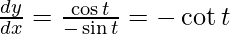
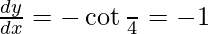
dy/dx = -1 & -dx/dy = 1
Now for t = π/4,
y1 = sin t = sin(π/4) = 1/√2
x1 = cos t = cos(π/4) = 1/√2
The point is (1/√2, 1/√2)
y – y1 = 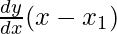
y – (1/√2) = -1(x – 1/√2)
y – 1/√2 = -x + 1/√2
x + y = √2 is the equation of normal is
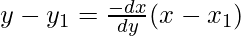
y – 1/√2 = 1(x – 1/√2)
x = y is the equation of normal.
Question 15. Find the equation of the tangent line to the curve y = x2 – 2x + 7 which is
(i) Parallel to line 2x – y + 9 = 0
(ii) Perpendicular to the line 5y – 15x = 13
Solution:
Given curve: y = x2 – 2x + 7
On differentiating w.r.t. x, we get
dy/dx = 2x – 2 -(1)
(i) Tangent is parallel to 2x – y + 9 = 0 that means,
Slope of tangent = slope of 2x – y + 9 = 0
y = 2x + 9
Slope = 2 -(Comparing with y = mx + e)
dy/dx = slope = 2
2x – 2 = 2
x1 = 2
Corresponding to x1 = 2,
y1 = x12 – 2x1 + 7
y1 = (2)2 – 2(2) + 7
y1 = 7
The point of contact is (2, 7).
Using point slope form, equation of tangent is
y – y1 = 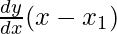
y – 7 = 2(x – 2)
y – 2x = 3 is the equation of tangent.
(ii) Tangent is perpendicular to the line 5y – 15x = 13
That means (slope of tangent) x (slope of line) = -1
For, slope of line 5y – 15x = 13
5y = 15x + 13
y = 3x + 13/15
Slope = 3
(Slope of tangent) x 3 = -1
Slope of tangent =-1/3
Now, y = x2 – 2x + 7
dy/dx = 2x – 2
On comparing dy/dx with slope, we get
2x – 2 = -1/3
6x – 6 = -1
6x = 5
x1 = 5/6
For x1 = 5/6,
y1 = x12 – 2x1 + 7
y1 = (5/6)12 – 2(5/6)1 + 7
y1 = 217/36
Now using point slope form, equation of tangent is
y – y1 = m(x – x1)
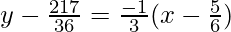
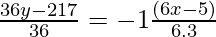
36y – 217 = -12x + 10
36y + 12x = 227 is the required equation of tangent.
Question 16. Show that the tangent to the curve y = 7x3 + 11 at the points where x = 2 and x = -2 are parallel.
Solution:
Given curve: y = 7x3 + 11
On differentiating w.r.t. x, we get
dy/dx = 21x2
dy/dx = 21(2)2 = 84
The slopes at x – 2 & -2 are the same,
Hence the tangent will be parallel to each other.
Question 17. Find the points on the curve y = x3 at which the slope of the tangent is equal to the y-coordinates of the point.
Solution:
Given curve: y = x3
On differentiating w.r.t. x, we get
dy/dx = 3x2 -(1)
Now let us assume that the point is (x1, y1)
dy/dx = 3x12
Also, slope of tangent at (x1, y1) is equal to y1.
So, 3x12 = y1 -(2)
Also, (x1, y1) lies on y = x3 x3,so
y1 = x13 -(3)
From eq(2) & (3)
3x12 = x13
3x12 = x13 = 0
x12(3 – x1) = 0
For x1 = 0, y1 = x13 = (0)3 = 0
One such point is (0, 0)
For x1 = 3, y1. = (3)3 = 27
Second point is (3, 27)
Question 18. For the curve y = 4x3 – 2x5, find all the points at which the tangent passes through the origin.
Solution:
Given curve: y = 4x3 – 3x5
Clearly at x = 0, y = 0, i.e the curve passes through origin.
Now the tangent also passes through origin.
Equation of a line passing through origin is y = mx.
Now tangent is touching the curve, so
y = mx will satisfy in curve.
mx = 4x3 – 2x5 -(1)
Now dy/dx = 12x2 – 10x4
Also m is the slope of tangent, so
m = 12x2 – 10x4 -(2)
From eq(1) & (2),
(12x2 – 10x4)x = 4x3 – 3x5
x3(12 – 10x2) = x3(4 – 2x2) -(3)
For the first point, x = 0
For x1 = 0, y1 = 4x13 – 2x15 = 0
So, (0, 0) is one such point
Now for other roots of 3
12 – 10x2 = 4 – 2x2
8 = 8x2
x2 = 1
x = ±1
For x2 = 1, y2 = 4x23 – 2x25 = 4(1)3 – 2(1)5 = 2
For x3 = -1, y3 = 4x33 – 2x35 = 4(-1)3 – 2(-1)5 = -2
The other points are(1, 2) & (-1, -2)
Question 19. Find the points on the curve x2 + y2 – 2x – 3 = 0 at which the tangents are parallel to the x-axis.
Solution:
Given curve: x2 + y2 – 2x – 3 = 0
On differentiating w.r.t. x, we get
3x + 2y(dy/dx) – 2 – 0 = 0
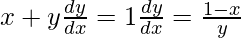
Given that the tangent are parallel to x-axis,
So, dy/dx = slope = 0
1 – x/y = 0
For x1 = 1,
x12 + y12 – 2x1 – 3 = 0
(1)2 + y12 – 2(1) – 3 = 0
y12 = 4
y12 = ≠2
The points are (1, 2) & (1, -2)
Question 20. Find the equation of the normal at the point (am2, am3) for the curve ay2 = x3.
Solution:
Given curve: ay2 = x3
On differentiating w.r.t. x, we get
2ay.dy/dx = 3x2
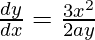 &
& 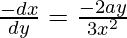
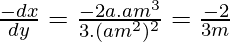
So, by point slope form, equation of normal is,
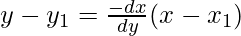
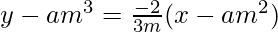
3my – 3am4 = -2x + 2am2
Hence, 3my + 2x = 2am2 + 3am4 is the required equation of normal.
Question 21. Find the equation of the normals to the curve y = x3 + 2x + 6 which are parallel to the line x + 14y + 4 = 0.
Solution:
Given curve: y = x3 + 2x + 6
On differentiating w.r.t. x, we get
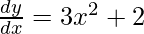
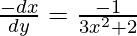 -(Slope of normal)
-(Slope of normal)
Now, the normal are parallel to x + 14y + 4 = 0
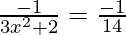
13 = 3x2 + 2
3x2 = 12 ⇒ x2 = 4
x = ±2
x1 = 2 & x2 = -2
For x1 = 2; y1 = 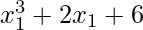 = (2)3 + 2(2) + 6 = 18
= (2)3 + 2(2) + 6 = 18
For x2 = -2; y2 = 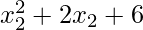 = (-2)3 + 2(-2) + 6 = -6
= (-2)3 + 2(-2) + 6 = -6
Normal through (2,18) is
y – 18 = 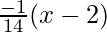
14y – 252 = -x + 2
14y + x = 254 is one such equation.
Normal through (-2, -6) is
y + 6 = 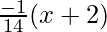
14y + 84 = -x – 2
14y + x + 86 = 0 is the other equation of normal.
Question 22. Find the equations of tangent and normal to the parabola y2 = 4ax at the point (at2, 2at).
Solution:
Given parabola: y2 = 4ax
On differentiating w.r.t. x, we get
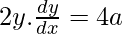
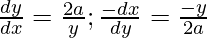
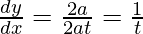
Now, by point slope form, equation of tangent is,
y – y1 = 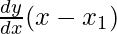
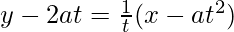
ty = x + at2 is the equation of tangent to the parabola y2 = 4ax at (at2, 2at)
Now 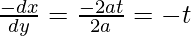
Now, by point slope form, equation of normal is,
y – y1 = 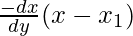
y – 2at = -t(x – at2)
y + xt = 2at + at3 is the equation of normal to the parabola y2 = 4ax at (at2, 2at)
Question 23. Prove that the curves x = y2 and xy = k cut at right angles if 8k2 = 1.
Solution:
Given curves: x = y2 & xy = k
Two curves intersect at right angles f the tangents through their point
intersection is perpendicular to each other.
Now if tangents are perpendicular their product of their slopes will be equal to -1.
Curve 1: x = y2
1 = 2y.dy/dx
dy/dx = 1/2 y = m1 -(1)
Curve 2: xy = k
y = k/x
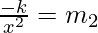
Let’s find their point of intersection
x = y2 & xy = k
k/y = y2
y = k1/3
x = y2
x = k2/3
The point is (k2/3, k1/3)
m1 = 1/2k1/3
For curves to be intersecting each other at right angles,
m1m2 = -1
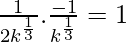
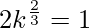
8k2 = 1
Hence proved
Question 24. Find the equations of the tangent and normal to the hyperbola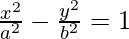 at the point (xo, yo).
at the point (xo, yo).
Solution:
Given curve: 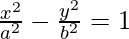
On differentiating both sides with respect to x,
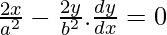
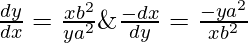
Now, 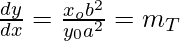
Equation of tangent by point slope form is,
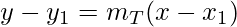
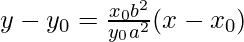
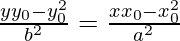
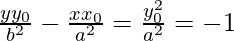 -((x0,y0) lie on
-((x0,y0) lie on 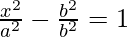 )
)
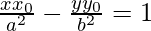 is the equation of tangent.
is the equation of tangent.
Now, 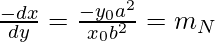
Equation of normal by point slope form is,
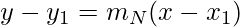
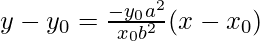
x0b2y – x0b2y0 = -y0a2x + y0a2x0
x0b2y + y0a2x = x0y0(a2 + b2) is the equation of normal
Question 25. Find the equation of the tangent to the curve y = 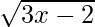 which is parallel to the line 4x – 2y + 5 = 0.
which is parallel to the line 4x – 2y + 5 = 0.
Solution:
Given curve: 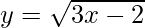
On differentiating w.r.t. x, we get
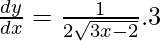
Now, it is given that the tangent is parallel to the line 4x – 2y + 5 = 0,
so their slopes must be equal.
Slope of 2y = 4x + 5 is 2.
So,
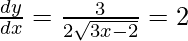
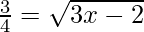
9/16 = 3x – 2
x1 = 41/48
Now, 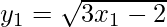
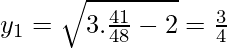
The point is (41/48, 3/4)
Now by point slope form, the equation of tangent will be
y – y1 = m(x – x1)
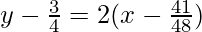
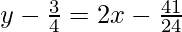
24y – 48x + 23 = 0 is the required equation of tangent.
Question 26. The slope of the normal to the curve y = 2x2 + 3 sin x at x = 0 is
(A) 3 (B) 1/3 (C)-3 (D) -1/3
Solution:
Given curve: y = 2x2 + 3 sin x
On differentiating w.r.t. x, we get
dy/dx = 4x + 3cos x
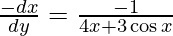 -(Slope of normal)
-(Slope of normal)
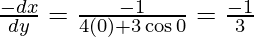
Hence, the correct option is D.
Question 27. The line y = x + 1 is a tangent to the curve y2 = 4x at the point
(A) (1, 2) (B) (2, 1) (C) (1, -2) (D) (-1, 2)
Solution:
Given curve: y2 = 4x
On differentiating w.r.t. x, we get
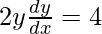
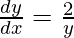
y = x + 1 is tangent, slope is 1, so, 2/y = 2
y1 = 2,
y12 = 4x1
x1 = 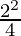
x1 = 1
So, (1, 2) is the point.
Hence, the correct option is A.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...