Class 12 NCERT Solutions- Mathematics Part I – Chapter 5 Continuity And Differentiability – Exercise 5.2
Last Updated :
03 Mar, 2021
Differentiate the function with respect to x in Question 1 to 8
Question 1. Sin(x2 + 5)
Solution:
y = sin(x2 + 5)
 =
= 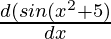
= cos(x2 + 5) × 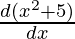
= cos(x2 + 5) × (2x)
dy/dx = 2xcos(x2 + 5)
Question 2. cos(sin x)
Solution:
y = cos(sin x)
 =
= 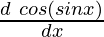
= -sin(sin x) × 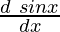
= -sin(sin x)cos x
Question 3. sin(ax + b)
Solution:
y = sin(ax + b)
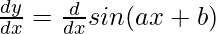
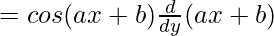
= a cos(ax + b)
Question 4. Sec(tan(√x)
Solution:
y = sec(tan√x)
 =
= 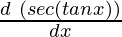
= sec(tan √x) × tan(√x) × 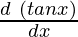
= sec (tan √x) × tan (tan √x) × sec2√x × 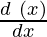
= sec(tan√x)tan(tan√x)(sec2√x)1/(2√x)
= 1/(2√x) × sec(tan√x)tan(tan√x)(sec2√x)
Question 5. 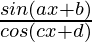
Solution:
y = 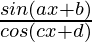
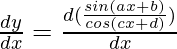
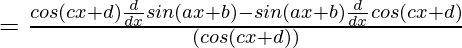
=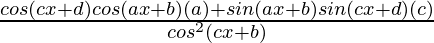
Question 6. cos x3.sin2(x5)
Solution:
y = cos x3.sin2(x5)
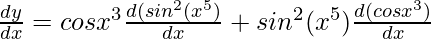
= 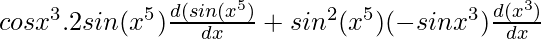
= cos x3.2sin(x5) .cos(x5(5x4)(5x4) – sin2(x5).sin x3.3x2
= 10x4 cos x3sin(x5)cos(x5) – 3x2 sin2(x5)sin x3
Question 7. 2√(cos(x2))
Solution:
y = 2√(cos(x2))
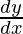 =
= 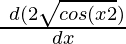
= 2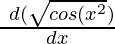
= 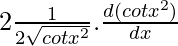
= 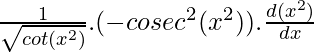
= 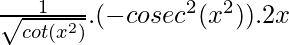
=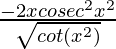
= 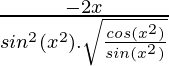
= 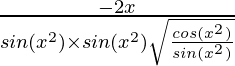
= 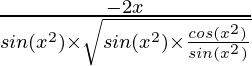
= 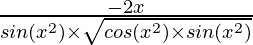
= 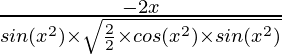
= 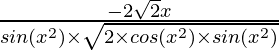
= 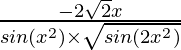
Question 8. cos (√x)
Solution:
y = cos (√x)
dy/dx = -sin√x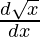
=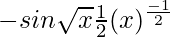
=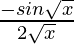
Question 9. Prove that the function f given by f(x) = |x – 1|, x ∈ R is not differentiable at x = 1.
Solution:
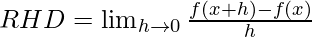
= 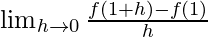
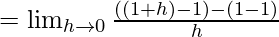
= 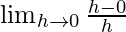
=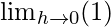
= +1
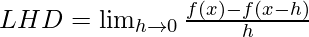
= 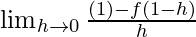
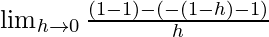
= 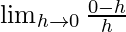
= 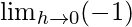
= -1
LHD ≠ RHD
Hence, f(x) is not differentiable at x = 1
Question 10. Prove that the greatest integer function defined by f(x) = [x], 0 < x < 3 is not differentiable at x = 1 and x = 2.
Solution:
Given: f(x) = [x], 0 < x < 3
LHS:
f'(1) = 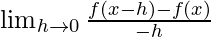
= 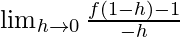
=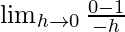
= ∞
RHS:
f'(1) = 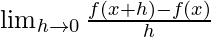
= 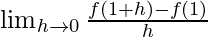
= 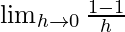
= 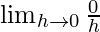
= 0
LHS ≠ RHS
So, the given f(x) = [x] is not differentiable at x = 1.
Similarly, the given f(x) = [x] is not differentiable at x = 2.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...