Class 12 NCERT Solutions- Mathematics Part I – Application of Derivatives – Exercise 6.1
Last Updated :
14 Feb, 2023
Question 1. Find the rate of change of the area of a circle with respect to its radius r when a) r=3cm b) r=4cm
Solution:
Given,
radius of circle=r=3cm
Now, we know that area=πr2=A
Rate of change of the area of a circle with respect to r=dA/dr
dA/dr=d/dr πr2=2πr
so, when r=3
dA/dr
=2π(3)=6π
when r=4
dA/dr
=2π(4)=8π
Question 2. The volume of a cube is increasing at the rate of cm3/s. How fast is the surface area increasing when the length of an edge is 12 cm?
Solution:
Given,
Rate of increase of the volume =8cm3/s
length of edge of cube=12cm=s
Now,
volume(v) of a cube with side length ‘s’
v=s3
Now,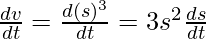 [chain rule]
[chain rule]
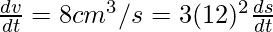
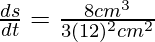
so, the rate of change of surface Area(A)
A=6s2
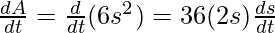

Question 3. The radius of a circle is increasing uniformly at rate of 3 cm/s. Find the rate at which the area of the circle is increasing when the radius is 10cm.
Solution:
Given,
rate of increase of radius = 3cm/s=r
so, 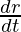 = 3cm\s
= 3cm\s
To find : Ratio of increase of Area(A=πr2)
 = π
= π 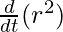 =2πr.
=2πr.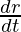 [chain rule]
[chain rule]
 =2π(10)3=60πr
=2π(10)3=60πr
Question 4. An edge of a variable cube is increasing at the rate of 3 cm/s. How fast is the volume of the cube increasing when the edge is 10cm long?
Solution:
Given: rate of increase of edge of cube,  =3cm/s
=3cm/s
To find: Rate of increase of volume (v) of the cube 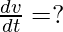
Now, 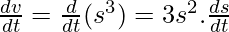 [chain rule]
[chain rule]
So, 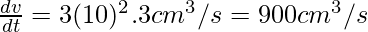
Question 5. A stone is dropped into a quiet lake and wave move in circles at the speed of 5cm/s. At the instant when the radius of the circular wave is 8cm, how fast is the enclosed area increasing?
Solution:
Given, Speed of water=rate of change of radius=5cm/s
To find: rate of increase of area=

 = π
= π 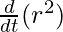 =2πr.
=2πr. 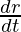 [chain rule]
[chain rule]
 = 2π(8)5cm2/s
= 2π(8)5cm2/s
=80πcm2/s
Question 6. The radius of a circle is increasing at the rate of 0.7cm/s. What is the rate of increase of its circumstances?
Solution:
Given: rate of increase of radius, 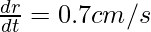
Circumference(P)=2πr
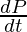 =2π.
=2π.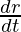 =2π.(0.7)
=2π.(0.7)
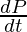 =1.4π cm/s or 4.4cm/s [taking π=22/7]
=1.4π cm/s or 4.4cm/s [taking π=22/7]
Question 7. The length x of a rectangle is decreasing at the rate of 5 cm/minute and the width y is increasing at the rate of 4 cm/minute. When x=8cm and y=6cm, find the rates of change of (a) the perimeter, and b) the area of the rectangle.
Solution:
Given: Rate of change of length, 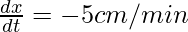
Rate of change of width, 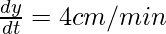
Now, perimeter P=2(r+y)
Area A=x.y
so, a) 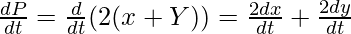
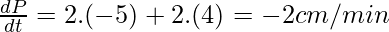
b)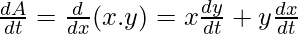 [x is decreasing, y is increasing]
[x is decreasing, y is increasing]
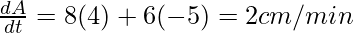
Question 8. A balloon, which always remains spherical on inflation, is being inflated by pumping in 900 cubic centimeters of gas per second. Find the rate at which the radius of the balloon increases when the radius is 15cm.
Solution:
Given, Amount of gas pumped in per second/ Rate of change of volume 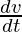 =900 cm3/s
=900 cm3/s
To find: Rate of change of radius,  when r=15cm.
when r=15cm.
v=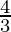 πr3
πr3
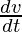 = 4πr2
= 4πr2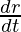
Now, 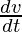 =4π(15)2.
=4π(15)2.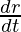
900=900π.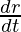
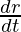 = 1/π cm/s
= 1/π cm/s
Question 9. A balloon, in which always remains spherical has a variable radius. Find the rate at which its volume is increasing with the radius when the later is 10cm.
Solution:
Let the radius be r & volume be v.
v=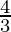 πr3
πr3
To find: Rate of change of volume with respect to
i.e 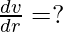
Now, 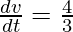 π
π .r3=4πr2
.r3=4πr2
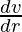 =400π cm2
=400π cm2
Question 10. A ladder 5m long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2 cm/s. How fast is its height on the wall decreasing when the foot of the ladder is 4m away from the wall?
Solution:
Given: Length of ladders=5m
In ∆ ABC, AC=5m, BC=4m, & ∠ABC=90°,
so by Pythagoras theorem,
AB=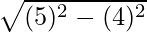 =3
=3
Now, let AB=x & BC=y
so, x2,y2=52 or x2,y2=25 ———1
Differentiating both sides of 1 by t, we get

or
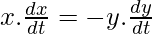
Now at BC=y=4,
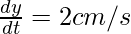
so 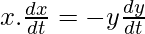
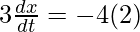
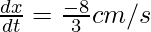 [negative sign means AB is decreasing]
[negative sign means AB is decreasing]
Question 11. A particle moves along the curve 6y=x3 + 2. Find the points on the curve at which the y coordinate is changing 8 times as fast as the x-coordinate.
Solution:
Given: curve 6y=x3+2 ————1
and 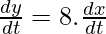 ———-2
———-2
Differentially 1 with respect to it, we get,
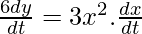
from 2 6.8.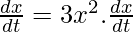
16=x2
x=±4 ————-3
Now for y coordinates, put 3
6y=x3+2
when x = -4
6y = -64+2
y = 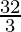
and, when x = 4
6y = 66
y = 11
Question 12. The radius of an air bubble is increasing at the rate of 1/2 cm/s. At what rate is the volume of the bubble increasing when the radius is 1 cm?
Solution:
Given: Rate of increase of radius  cm/s
cm/s
To Find: Rate of increase of volume,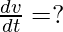
Now, v=4/3πr3
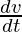 =
=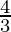 π
π 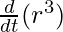 =4πr2
=4πr2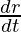
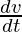 =4π(1)2.
=4π(1)2.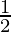 cm3/s
cm3/s
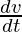 =2π cm3/s
=2π cm3/s
Question 13. A balloon, which always remains spherical, has a variable diameter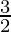 (2x+1). Find the rate of change of its volume with respect to x.
(2x+1). Find the rate of change of its volume with respect to x.
Solution:
Given: Diameter of sphere=3/2(2x+1)=d
So, radius of the sphere will be d/2=3/4(2x+1)=r
 (2)
(2)
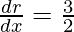
Now, volume =4/3πr3
Rate of change of volume with respect to radius
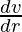 =
=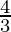 π
π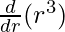 =4πr2
=4πr2
 = 4π(
= 4π(
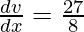 π (2x+1)2
π (2x+1)2
Question 14. Sand is pouring from a pipe at the rate of 12 cm3/s. The falling sand forms a cone on the ground in such a way that the height of the cone is always one-sixth of the radius of the base. How fast is the height of the cone increasing when the height is 4cm?
Solution:
Given: Rate of falling sand=12cm3/s
Now this rate is basically the rate of change of the cone.
so, 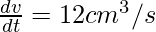
Now, radius =r
height =r
height is always one-sixth of the radius so,
h=r/6 or r=6h
To find : Rate of change of height =dh/dt=?
Now, volume v=1/3πr2h=1/3.π(6h)2.h
v=12πh3
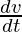 =12π
=12π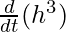 =12π3h2.
=12π3h2.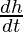
12 =36π.(4)2.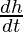
 = π
= π 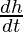
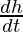 =1 / 48π cm/s
=1 / 48π cm/s
Question 15. The total cost C(x) in Rupees associated with the production of x units of an item is given by C(x)=0.003x2+15x+4000. Find the marginal cost when 17 units are produced.
Solution:
Given: c(x)=0.007x3-0.003x2+15c+4000
Now change in total cost with respect to units is known as marginal cost i.e 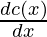
![Rendered by QuickLaTeX.com \frac{d[(x)]}{dx}=\frac{d}{dx}(0.007x^3-0.003x^2+15x+4000)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3789de7d6c698bc63216cc53baa459e2_l3.png)
Marginal cost=0.021x2-0.006x+15
Marginal cost when 17 units are produced
=0.221(17)2-0.006(17)+15
=6.069-0.102+15
=20.967
Question 16. The total revenue in Rupees from the scale of x units of a product is given by R(x)=13x3+26x+15. Find the marginal revenue when x=7.
Solution:
Marginal revenue is the rate of change of total revenue with respect to no. of units.
So, Marginal revenue =![Rendered by QuickLaTeX.com \frac{d}{dx}[R(x)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-25e9c8f253fb9b1042a9e9ddb96f32de_l3.png)
Marginal revenue=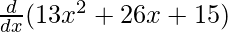
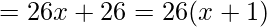
Marginal revenue when (x=7)
=26 (8)
=208
Question 17. The rate of change of area of circle with respect to its radius r at r= 6cm is (A) 10π (B) 12π (C) 8π (D) 11π.
Solution:
Area, A=πr2,where r is the radius
Rate of change of area with respect to its radius r is,
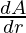 =π
=π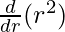 =2πr
=2πr
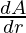 =2π(6)=12π
=2π(6)=12π
Question 18. The total revenue in Rupees received from the sale of x units of a product is given by R(x)=3x2 +36x+5. The marginal revenue, when x=15 is (A) 116 (B) 96 (C) 90 (D) 126
Solution:
Marginal Revenue=
Marginal Revenue=6x + 36
Marginal Revenue at x=15 is 6 (15)+36=126
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...