Class 12 NCERT Solutions- Mathematics Part I – Chapter 2 Inverse Trigonometric Functions – Exercise 2.2 | Set 2
Last Updated :
03 Apr, 2024
Content of this article has been merged with Chapter 2 Inverse Trigonometric Functions – Exercise 2.2 as per the revised syllabus of NCERT.
Find the values of each of the following:
Question 11. tan−1[2cos(2sin−11/2)]
Solution:
Let us assume that sin−11/2 = x
So, sinx = 1/2
Therefore, x = π/6 = sin−11/2
Therefore, tan−1[2cos(2sin−11/2)] = tan−1[2cos(2 * π/6)]
= tan−1[2cos(π/3)]
Also, cos(π/3) = 1/2
Therefore, tan−1[2cos(π/3)] = tan−1[(2 * 1/2)]
= tan−1[1] = π/4
Question 12. cot(tan−1a + cot−1a)
Solution:
We know, tan−1x + cot−1x = π/2
Therefore, cot(tan−1a + cot−1a) = cot(π/2) =0
Question 13. ![Rendered by QuickLaTeX.com tan\frac{1}{2}[sin^{-1}\frac{2x}{1+x^2}+cos^{-1}\frac{1-y^2}{1+y^2}],|x|<1,y>0,xy<1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d7102f777cf47f446e983200509572f9_l3.png)
Solution:
We know, 2tan-1x = 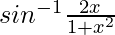 and 2tan-1y =
and 2tan-1y = ![Rendered by QuickLaTeX.com cos^{-1}[\frac{1 - y^2 }{1+y^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1450f93bf6cd45227d3d63861b97f779_l3.png)
![Rendered by QuickLaTeX.com \therefore tan\frac{1}{2}[sin^{-1}\frac{2x}{1+x^2}+cos^{-1}\frac{1-y^2}{1+y^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-725470d0ce62eda417a57c8b169c5692_l3.png)
= tan(1/2)[2(tan−1x + tan−1y)]
= tan[tan−1x + tan−1y]
Also, tan−1x + tan−1y = 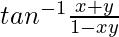
Therefore, tan[tan−1x + tan−1y] = ![Rendered by QuickLaTeX.com tan[tan^{-1}\frac{x+y}{1-xy}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c7a52f0872ab94201d3a60f046de1ce2_l3.png)
= (x + y)/(1 – xy)
Question 14. If sin(sin−11/5 + cos−1x) = 1 then find the value of x
Solution:
sin−11/5 + cos−1x = sin−11
We know, sin−11 = π/2
Therefore, sin−11/5 + cos−1x = π/2
sin−11/5 = π/2 – cos−1x
Since, sin−1x + cos−1x = π/2
Therefore, π/2 – cos−1x = sin−1x
sin−11/5 = sin−1x
So, x = 1/5
Question 15. If 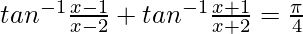 , then find the value of x
, then find the value of x
Solution:
We know, tan−1x + tan−1y = 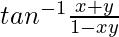
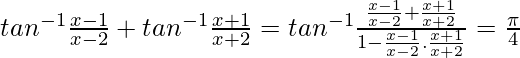
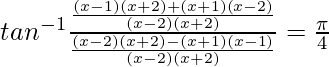
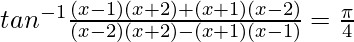
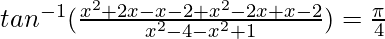
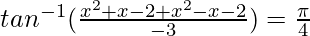
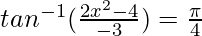
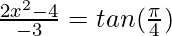
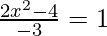
2x2 – 4 = -3
2x2 – 4 + 3 = 0
2x2 – 1 = 0
x2 = 1/2
x = 1/√2, -1/√2
Find the values of each of the expressions in Exercises 16 to 18.
Question 16. sin − 1(sin2π/3)
Solution:
We know that sin−1(sinθ) = θ when θ ∈ [-π/2, π/2], but 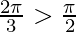
So, sin − 1(sin2π/3) can be written as ![Rendered by QuickLaTeX.com sin^{-1}[sin(\pi-\frac{2\pi}{3})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a9bc00a25ad23e9dca5d2bac22df909c_l3.png)
sin − 1(sinπ/3) here 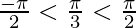
Therefore, sin − 1(sinπ/3) = π/3
Question 17. tan−1(tan3π/4)
Solution:
We know that tan−1(tanθ) = θ when 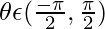 but
but 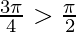
So, tan−1(tan3π/4) can be written as tan−1(-tan(-3π/4))
= tan−1[-tan(π – π/4)]
= tan−1[-tan(π/4)]
= –tan−1[tan(π/4)]
= – π/4 where 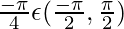
Question 18. 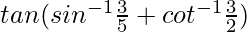
Solution:
Let us assume 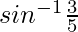 = x , so sinx = 3/5
= x , so sinx = 3/5
We know, 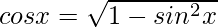
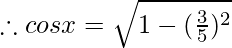
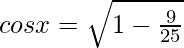
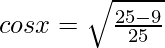
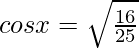
cosx = 4/5
We know, 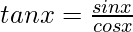
So, 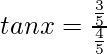
tanx = 3/4
Also, 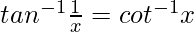
Hence, 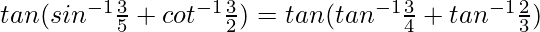
tan-1x + tan-1y = 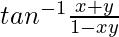
So, 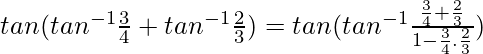
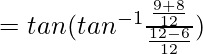
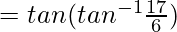
= 17/6
Question 19. cos−1(cos7π/6) is equal to
(i) 7π/6 (ii) 5π/6 (iii)π/3 (iv)π/6
Solution:
We know that cos−1(cosθ) = θ, θ ∈ [0, π]
cos−1(cosθ) = θ, θ ∈ [0, π]
Here, 7π/6 > π
So, cos−1(cos7π/6) can be written as cos−1(cos(-7π/6))
= cos−1[cos(2π – 7π/6)] [cos(2π + θ) = θ]
= cos−1[cos(5π/6)] where 5π/6 ∈ [0, π]
Therefore, cos−1[cos(5π/6)] = 5π/6
Question 20. ![Rendered by QuickLaTeX.com sin[\frac{\pi}{3} - sin^{-1}(-\frac{1}{2} )]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2b0e825238a7b4df36dd78d4540e65d9_l3.png)
(i) 1/2 (ii) 1/3 (iii) 1/4 (iv) 1
Solution:
Let us assume sin-1(-1/2)= x, so sinx = -1/2
Therefore, x = -π/6
Therefore, sin[π/3 – (-π/6)]
= sin[π/3 + (π/6)]
= sin[3π/6]
= sin[π/2]
= 1
Question 21. 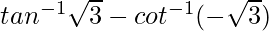 is equal to
is equal to
(i) π (ii) -π/2 (iii)0 (iv)2√3
Solution:
We know, cot(−x) = −cotx
Therefore, tan-13 – cot-1(-3) = tan-13 – [-cot-1(3)]
= tan-13 + cot-13
Since, tan-1x + cot-1x = π/2
Tan-13 + cot-13 = -π/2
Share your thoughts in the comments
Please Login to comment...