Class 12 NCERT Solutions- Mathematics Part I – Chapter 4 Determinants – Exercise 4.3
Last Updated :
03 Apr, 2024
Write minors and cofactors of the elements of the following determinants:
Question 1.
(i) 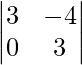
(ii) 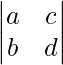
Solution:
(i) 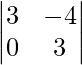
Finding minors of the elements of the determinant:
Let us assume Mij is Minors of elements aij
M11 = Minor of elements a11 = 3
M12 = Minor of elements a12 = 0
M21 = Minor of elements a21 = −4
M22 = Minor of elements a22 = 2
Finding cofactor of aij
Let us assume cofactor of aij is Aij Mij
A11 = (−1)1+1 M11 = (−1)2 (3) = 3
A12 = (−1)1+2 M12 = (−1)3 (0) = 0
A21 = (−1)2+1 M21 = (−1)3 (−4) = 4
A22 = (−1)2+2 M22 = (−1)4 (2) = 2
(ii) 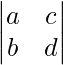
Finding minors of the elements of the determinant:
Let us assume Mij is Minors of elements aij
M11 = Minor of element a11 = d
M12 = Minor of elements a12 = b
M21 = Minor of elements a21 = c
M22 = Minor of elements a22 = a
Finding cofactor of aij
Let us assume cofactor of aij is Aij, which is (−1)i+j Mij
A11 = (−1)1+1 M11 = (−1)2 (d) = d
A12 = (−1)1+2 M12 = (−1)3 (b) = −b
A21 = (−1)2+1 M21 = (−1)3 (c) = −c
A22 = (−1)2+2 M22 = (−1)4 (a) = a
Question 2.
(i)
(ii)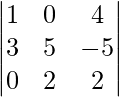
Solution:
(i) 
Let us find the Minors and cofactors of the elements:
Assume, Mij is minor of element aij and Aij is cofactor of aij
M11 = Minor of elements a11 = = 1 − 0 = 1 and A11 = 1
= 1 − 0 = 1 and A11 = 1
M12 = Minor of elements a12 = = 0 − 0 = 0 and A12 = 0
= 0 − 0 = 0 and A12 = 0
M13 = Minor of elements a13 = = 0 − 0 = 0 and A13 = 0
= 0 − 0 = 0 and A13 = 0
M21 = Minor of elements a21 = = 0 − 0 = 0 and A21 = 0
= 0 − 0 = 0 and A21 = 0
M22 = Minor of elements a22 = = 1 − 0 = 1 and A22 = 1
= 1 − 0 = 1 and A22 = 1
M23 = Minor of elements a23 = = 0 − 0 = 0 and A23 = 0
= 0 − 0 = 0 and A23 = 0
M31 = Minor of elements a31 = = 0 − 0 = 0 and A31 = 0
= 0 − 0 = 0 and A31 = 0
M32 = Minor of elements a32 = = 0 − 0 = 0 and A32 = 0
= 0 − 0 = 0 and A32 = 0
M33 = Minor of elements a33 = = 1 − 0 = 1 and A33 = 1
= 1 − 0 = 1 and A33 = 1
(ii) 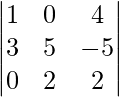
Let us find the Minors and cofactors of the elements:
Assume, Mij is minor of element aij and Aij is cofactor of aij
M11 = Minor of elements a11 =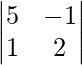 = 10 − (−1) = 11 and A11 = 11
= 10 − (−1) = 11 and A11 = 11
M12 = Minor of elements a12 =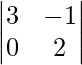 = 6 − 0 = 6 and A12 = −6
= 6 − 0 = 6 and A12 = −6
M13 = Minor of elements a13 =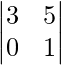 = 3 − 0 = 3 and A13 = 3
= 3 − 0 = 3 and A13 = 3
M21 = Minor of elements a21 =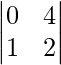 = 0 − 4 = −4 and A21 = 4
= 0 − 4 = −4 and A21 = 4
M22 = Minor of elements a22 =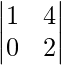 = 2 − 0 = 2 and A22 = 2
= 2 − 0 = 2 and A22 = 2
M23 = Minor of elements a23 = = 1 − 0 = 1 and A23 = −1
= 1 − 0 = 1 and A23 = −1
M31 = Minor of elements a31 =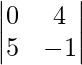 = 0 − 20 = −20 and A31 = −20
= 0 − 20 = −20 and A31 = −20
M32 = Minor of elements a32 =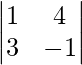 = −1 − 12 = −13 and A32 = 13
= −1 − 12 = −13 and A32 = 13
M33 = Minor of elements a33 = = 5 − 0 = 5 and A33 = 5
= 5 − 0 = 5 and A33 = 5
Question 3. Using Cofactors of elements of second row, evaluate △?
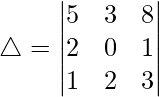
Solution:
Finding the Cofactors of elements of second row:
A21 = Cofactor of elements a21 = (−1)2+1  = (−1)3 (9 − 16) = 7
= (−1)3 (9 − 16) = 7
A22 = Cofactor of elements a22 = (−1)2+2  = (−1)4 (15 − 8) = 7
= (−1)4 (15 − 8) = 7
A23 = Cofactor of elements a23 = (−1)2+3 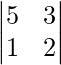 = (−1)5 (10 − 3) = 7
= (−1)5 (10 − 3) = 7
Now, △ = a21 A21 + a22 A22 + a23 A23 = 14 + 0 − 7 = 7
Question 4. Using Cofactors of elements of third column, evaluate △?
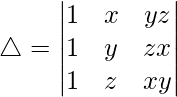
Solution:
Finding the Cofactors of elements of third column:
A13 = Cofactor of elements a13 = (−1)1+3 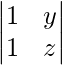 = (−1)4 (z − y) = −y
= (−1)4 (z − y) = −y
A23 = Cofactor of elements a23 = (−1)2+3 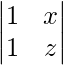 = (−1)5 (z − x) = x − z
= (−1)5 (z − x) = x − z
A33 = Cofactor of elements a33 = (−1)3+3 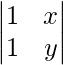 = (−1)6 (y − x) = y − x
= (−1)6 (y − x) = y − x
Now, △ = a13 A13 + a23 A23 + a33 A33
= yz (z − y) + zx (x − z) + xy (y − x)
= (yz2 − y2z) + (xy2 − xz2) + (xz2 − x2y)
= (y − z)[−yz + x(y + z) − x2]
= (y − z)[−yz + x (z − x) + x (z − x)]
= (x − y)(y − x)(z − x)
Question 5. If  and Aij is cofactor of aij then value of △ is given by:
and Aij is cofactor of aij then value of △ is given by:
(A) a11A31 + a12A32 + a13A33
(B) a11A11 + a12A21 + a13A31
(C) a21A11 + a22A12 + a23A13
(D) a11A11 + a21A21 + a31A31
Solution:
Option (D) is correct.
Share your thoughts in the comments
Please Login to comment...