Class 12 NCERT Solutions- Mathematics Part I – Chapter 3 Matrices – Miscellaneous Exercise on Chapter 3
Last Updated :
03 Apr, 2024
Question 1. If A and B are symmetric matrices, prove that AB – BA is a skew-symmetric matrix.
Solution:
As, it is mentioned that A and B are symmetric matrices,
A’ = A and B’ = B
(AB – BA)’ = (AB)’ – (BA)’ (using, (A-B)’ = A’ – B’)
= B’A’ – A’B’ (using, (AB)’ = B’A’)
= BA – AB
(AB – BA)’ = – (AB – BA)
Hence, AB – BA is a skew symmetric matrix
Question 2. Show that the matrix B′AB is symmetric or skew-symmetric according as A is symmetric or skew-symmetric.
Solution:
Let’s take A as symmetric matrix
A’ = A
Then,
(B′AB)’ = {B'(AB)}’
= (AB)’ (B’)’ (using, (AB)’ = B’A’)
= B’A’ (B) (using, (AB)’ = B’A’ and (B’)’ = B)
= B’A B
As, here (B′AB)’ = B’A B. It is a symmetric matrix.
Let’s take A as skew matrix
A’ = -A
Then,
(B′AB)’ = {B'(AB)}’
= (AB)’ (B’)’ (using, (AB)’ = B’A’)
= B’A’ (B) (using, (AB)’ = B’A’ and (B’)’ = B)
= B'(-A) B
= – B’A B
As, here (B′AB)’ = -B’A B. It is a skew matrix.
Hence, we can conclude that B′AB is symmetric or skew symmetric according as A is symmetric or skew symmetric.
Question 3. Find the values of x, y, z if the matrix 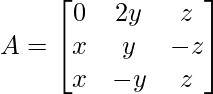 satisfy the equation A′A = I
satisfy the equation A′A = I
Solution:
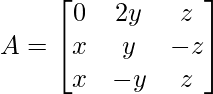
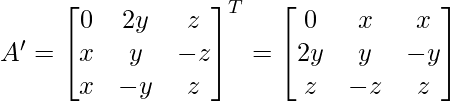
A’A = 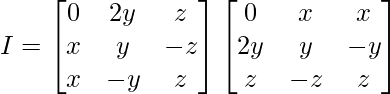
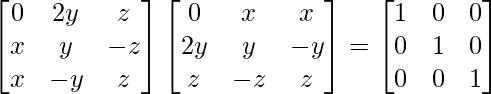
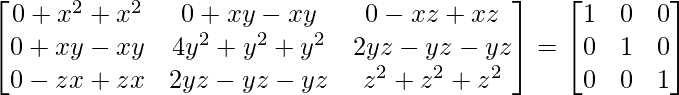
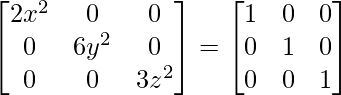
By evaluating the values, we have
2x2 = 1
x = ± 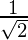
6y2 = 1
y = ± 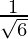
3z2 = 1
z = ± 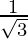
Question 4: For what values of x : 
Solution:

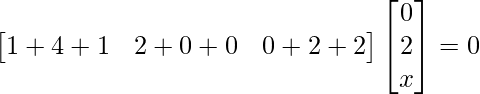
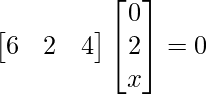
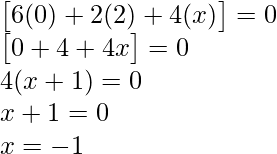
Question 5: If 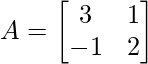 , show that A2 – 5A + 7I = 0.
, show that A2 – 5A + 7I = 0.
Solution:
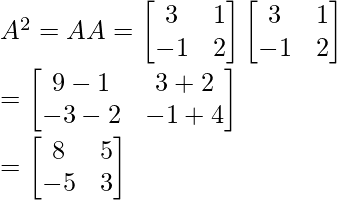
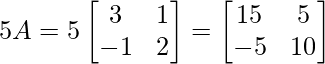
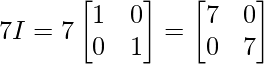
A2 – 5A + 7I = 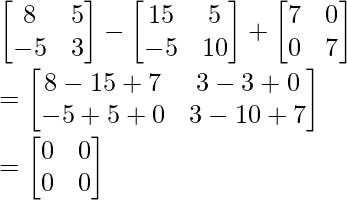
Hence proved!
Question 6: Find x, if 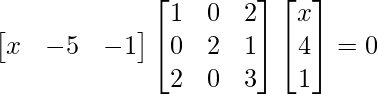
Solution:
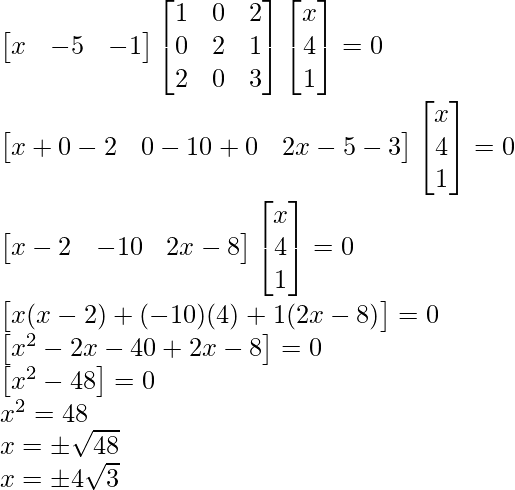
Question 7: A manufacturer produces three products x, y, z which he sells in two markets.
Annual sales are indicated below:
| Market | Products |
| I | 10,000 | 2,000 | 18,000 |
| II | 6,000 | 20,000 | 8,000 |
(a) If unit sale prices of x, y and z are ₹ 2.50, ₹ 1.50 and ₹ 1.00, respectively, find the total revenue in each market with the help of matrix algebra.
Solution:
Total revenue in market I and II can be arranged from given data as follows:
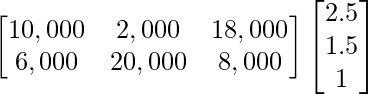
After multiplication, we get
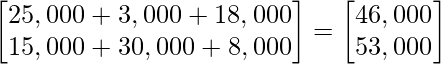
Hence, the total revenue in Market I and market II are ₹ 46,000 and ₹ 53,000 respectively.
(b) If the unit costs of the above three commodities are ₹ 2.00, ₹ 1.00 and 50 paise respectively. Find the gross profit.
Solution:
Total cost prices of all the products in market I and market II can be arranged from given data as follows:
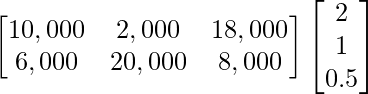
After multiplication, we get
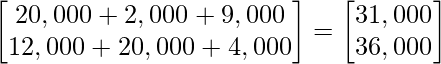
As, Profit earned = Total revenue – Cost price
Profit earned 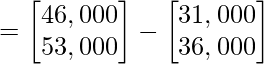
Profit earned = 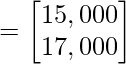
Hence, profit earned in Market I and market II are ₹ 15,000 and ₹ 17,000 respectively. Which is equal to ₹ 32,000
Question 8. Find the matrix X so that 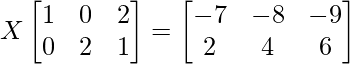
Solution:
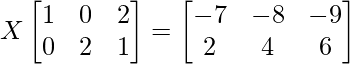
Here, the RHS is a 2×3 matrix and LHS is 2×3. So, X will be 2×2 matrix.
Let’s take X as,
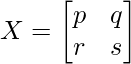
Now solving the matrix, we have
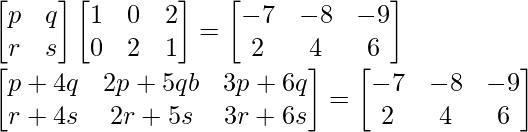
Equating each of them, we get
p+4q = -7 ………..(1)
2p+5q = -8 ………….(2)
3p + 6q = -9
r + 4s = 2 …………(3)
2r + 5s = 4 ……………(5)
3r + 6s = 6
Solving (1) and (2), we get
p = 1 and q = -2
Solving (3) and (4), we get
r = 2 and s = 0
Hence, matrix X is
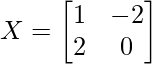
Choose the correct answer in the following questions:
Question 9: If 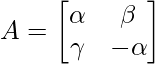 is such that A² = I, then
is such that A² = I, then
(A) 1 + α² + βγ = 0
(B) 1 – α² + βγ = 0
(C) 1 – α² – βγ = 0
(D) 1 + α² – βγ = 0
Solution:
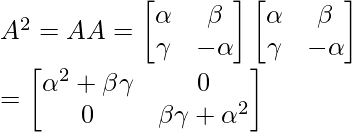
As, A2 = I
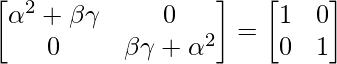
α² + βγ = 1
1 – α² – βγ = 0
Hence, Option (C) is correct.
Question 10. If the matrix A is both symmetric and skew symmetric, then
(A) A is a diagonal matrix
(B) A is a zero matrix
(C) A is a square matrix
(D) None of these
Solution:
If the matrix A is both symmetric and skew symmetric, then
A = A’
and A = -A
Only zero matrix satisfies both the conditions.
Hence, Option (B) is correct.
Question 11. If A is square matrix such that A2 = A, then (I + A)³ – 7 A is equal to
(A) A
(B) I – A
(C) I
(D) 3A
Solution:
(I + A)³ – 7 A = I3 + A3 + 3A^2 + 3AI^2 – 7A
= I3 + A3 + 3A2 + 3A – 7A
= I + A3 + 3A2 – 4A
As, A2 = A
A3 = A2A = AA = A
So, I + A3 + 3A2 – 4A = I + A + 3A – 4A = I
Hence, Option (C) is correct.
Deleted Questions
Let 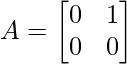 , show that (aI + bA)n = an I + nan – 1 bA, where I is the identity matrix of order 2 and n ∈ N.
, show that (aI + bA)n = an I + nan – 1 bA, where I is the identity matrix of order 2 and n ∈ N.
Solution:
Using mathematical induction,
Step 1: Let’s check for n=1
(aI + bA)n = (aI + bA)1 = (aI + bA)
anI + nan – 1 bA = aI + 1a1 – 1 bA = (aI + bA)
It is true for P(1)
Step 2: Now take n=k
(aI + bA)k = akI + kak – 1 bA …………………(1)
Step 3: Let’s check whether, its true for n = k+1
(aI + bA)k+1 = (aI + bA)k (aI + bA)
= (akI + kak – 1 bA) (aI + bA)
= ak+1I×I + kak bAI + ak bAI + kak-1 b2AA
AA = 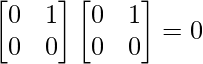
= ak+1I×I + kak bAI + ak bAI + 0
= ak+1I + (k+1)ak+1-1 bA
= P(k+1)
Hence, P(n) is true.
If 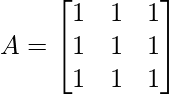 , prove that
, prove that 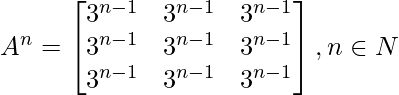
Solution:
Using mathematical induction,
Step 1: Let’s check for n=1
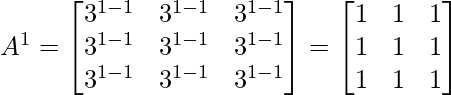
It is true for P(1)
Step 2: Now take n=k
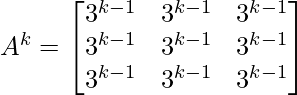
Step 3: Let’s check whether, its true for n = k+1

= P(k+1)
Hence, P(n) is true.
If 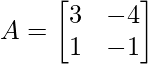 , prove that
, prove that 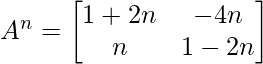 ,where n is any positive integer.
,where n is any positive integer.
Solution:
Using mathematical induction,
Step 1: Let’s check for n=1
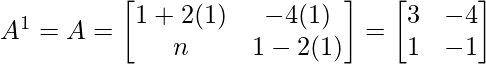
It is true for P(1)
Step 2: Now take n=k
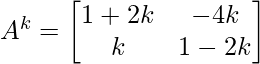
Step 3: Let’s check whether, its true for n = k+1
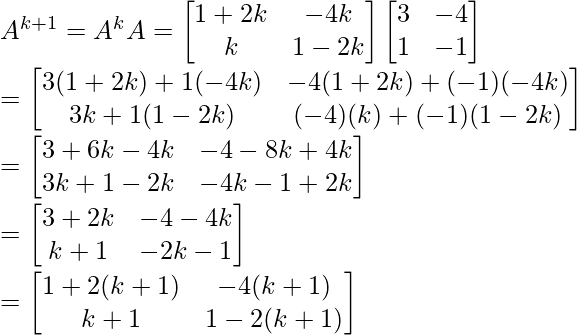
= P(k+1)
Hence, P(n) is true.
If A and B are square matrices of the same order such that AB = BA, then prove by induction that ABn = BnA. Further, prove that (AB)n = AnBn for all n ∈ N.
Solution:
Using mathematical induction,
Step 1: Let’s check for n=1
ABn = AB1 = AB
BnA = B1A = BA
It is true for P(1)
Step 2: Now take n=k
ABk = BkA
Step 3: Let’s check whether, its true for n = k+1
AB(k+1) = ABkB
= BkAB
= Bk+1 A
= P(k+1)
Hence, P(n) is true.
Now, for (AB)n = AnBn
Using mathematical induction,
Step 1: Let’s check for n=1
(AB)1 = AB
B1A1 = BA
It is true for P(1)
Step 2: Now take n=k
(AB)k = AkBk
Step 3: Let’s check whether, its true for n = k+1
(AB)(k+1) = (AB)k(AB)
= AkBk AB
= Ak+1 Bk+1
= (AB)k+1
= P(k+1)
Hence, P(n) is true.
Share your thoughts in the comments
Please Login to comment...