Class 12 NCERT Solutions- Mathematics Part I – Chapter 6 Application of Derivatives – Exercise 6.4

Read

Discuss

Question 1. Using differentials, find the approximate value of each of the following up to 3 places of decimal.

(i)√25.3

(ii)√49.5

(iii) √0.6

(iv) (0.009)^1/3

(v) (0.999)^1/10

(vi) (15)^1/4

(vii) (26)^1/3

(viii) (255)^1/4

(ix) (82)^1/4

(x) (401)^1/2

(xi) (0.0037)^1/2

(xii) (26.57)^1/3

(xiii) (81.5)^1/4

(xiv) (3.968)^3/2

(xv) (32.15)^1/5

Solution:

(i) √25.3

We take y = √x

Let x = 25 and △x = 0.3

△y = √(x +△x) – √x

= √25.3 – √25

= √25.3 – 5

or √25.3 = 5 + △y

Here, dy is approximately equal to △y

dy = (dy/dx)△x

= $\frac{1}{2√x}(0.3)$

= $\frac{1}{2√25}(0.3)$

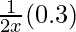
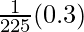
= 0.3/10

= 0.03

Hence, the approximate value of√25.3 = 5 + 0.03 = 5.03

(ii)√49.5

We take y = √x

Let x = 49 and △x = 0.5

△y = √(x +△x) – √x

= √49.5 – √49

= √49.5 – 7

or √49.5 = 7 + △y

Here, dy is approximately equal to △y

dy = (dy/dx)△x

= $\frac{1}{2√x}(0.5)$

= $\frac{1}{2√49}(0.5)$

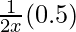
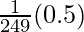
= 0.5/14

= 0.0357

Hence, the approximate value of √49.5 = 7 + 0.0357 = 7.0357

(iii) √0.6

We take y = √x

Let x = 0.64 and △x = -0.04

△y = √(x +△x) – √x

= √0.6 – √0.64

= √0.6 – 0.8

or √0.6 = 0.8 + △y

Here, dy is approximately equal to △y

dy = (dy/dx)△x

= $\frac{1}{2√x}(-0.04)$

= $\frac{1}{2√0.64}(-0.04)$

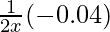
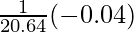
= -0.04/1.6

= -0.025

Hence, the approximate value of √0.6 = 0.8 – 0.025 = 0.775

(iv) (0.009)^1/3

We take y = x^1/3

Let x = 0.008 and △x = 0.001

△y = (x +△x)^1/3 – x^1/3

= (0.009)^1/3 – (0.008)^1/3

= (0.009)^1/3 – 0.2

or (0.009)^1/3= 0.2 + △y

Here, dy is approximately equal to △y

dy = (dy/dx)△x

= $\frac{0.001}{3x^{\frac{2}{3}}}$

= $\frac{0.001}{3(0.008)^{\frac{2}{3}}}$

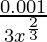
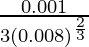
= 0.0083

Hence, the approximate value of (0.009)^1/3 = 0.2 + 0.0083 = 0.2083

(v) (0.999)^1/10

We take y = x^1/10

Let x = 1 and △x = -0.001

△y = (x +△x)^1/10 – x^1/10

= (1)^1/10 – (0.001)^1/10

= (1)^1/10 – 1

or (1)^1/10= 1 + △y

Here, dy is approximately equal to △y

dy = (dy/dx)△x

= $\frac{-0.001}{10x^{\frac{9}{10}}}$

= $\frac{-0.001}{10(1)^{\frac{9}{10}}}$

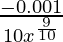
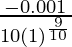
= -0.0001

Hence, the approximate value of (0.999)^1/10 = 1 – 0.0001 = 0.9999

(vi) (15)^1/4

We take y = x^1/4

Let x = 16 and △x = -1

△y = (x +△x)^1/4 – x^1/4

= (15)^1/4 – (16)^1/4

= (15)^1/4 – 2

or (15)^1/4= 2 + △y

Here, dy is approximately equal to △y

dy = (dy/dx)△x

= $\frac{-1}{4x^{\frac{3}{4}}}$

= $\frac{-1}{4(16)^{\frac{3}{4}}}$

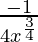
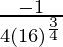
= -1/32

Hence, the approximate value of (15)^1/4 = 2 – 1/32 = 1.9687

(vii) (26)^1/3

We take y = x^1/3

Let x = 27 and △x = -1

△y = (x +△x)^1/3 – x^1/3

= (26)^1/3 – (27)^1/3

= (26)^1/3 – 3

or (26)^1/3= 3 + △y

Here, dy is approximately equal to △y

dy = (dy/dx)△x

= $\frac{-1}{3x^{\frac{2}{3}}}$

= $\frac{-1}{3(27)^{\frac{2}{3}}}$

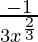
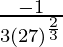
= -1/27

Hence, the approximate value of (26)^1/3= 3 – 1/27 = 2.962

(viii) (255)^1/4

We take y = x^1/4

Let x = 256 and △x = -1

△y = (x +△x)^1/4 – x^1/4

= (255)^1/4 – (256)^1/4

= (255)^1/4 – 4

or (255)^1/4= 4 + △y

Here, dy is approximately equal to △y

dy = (dy/dx)△x

= $\frac{-1}{4x^{\frac{3}{4}}}$

= $\frac{-1}{4(256)^{\frac{3}{4}}}$

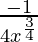
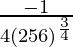
= -1/256

Hence, the approximate value of (255)^1/4= 4 – 1/256 = 3.996

(ix) (82)^1/4

We take y = x^1/4

Let x = 81 and △x = 1

△y = (x +△x)^1/4 – x^1/4

= (82)^1/4 – (81)^1/4

= (82)^1/4 – 3

or (82)^1/4= 3 + △y

Here, dy is approximately equal to △y

dy = (dy/dx)△x

= $\frac{1}{4x^{\frac{3}{4}}}$

= $\frac{1}{4(81)^{\frac{3}{4}}}$

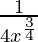
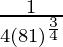
= 1/108

Hence, the approximate value of (82)^1/4= 3 + 1/108 = 3.009

(x) (401)^1/2

We take y = x^1/2

Let x = 400 and △x = 1

△y = (x +△x)^1/2 – x^1/2

= (401)^1/2 – (400)^1/2

= (401)^1/2 – 20

or (401)^1/2= 20 + △y

Here, dy is approximately equal to △y

dy = (dy/dx)△x

= $\frac{1}{2\sqrt{x}}$

= $\frac{1}{2\sqrt{400}}$

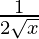
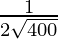
= 1/40

Hence, the approximate value of (401)^1/2= 20 + 1/40 = 20.025

(xi) (0.0037)^1/2

We take y = x^1/2

Let x = 0.0036 and △x = 0.0001

△y = (x +△x)^1/2 – x^1/2

= (0.0037)^1/2 – (0.0036)^1/2

= (0.0037)^1/2 – 0.06

or (0.0037)^1/2= 0.06 + △y

Here, dy is approximately equal to △y

dy = (dy/dx)△x

= $\frac{0.0001}{2\sqrt{x}}$

= $\frac{0.0001}{2\sqrt{0.0036}}$

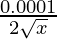
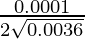
= 0.0001/0.12

Hence, the approximate value of (0.0037)^1/2= 0.06 + 0.0001/0.12 = 0.0608

(xii) (26.57)^1/3

We take y = x^1/3

Let x = 27 and △x = -0.43

△y = (x +△x)^1/3 – x^1/3

= (26.57)^1/3 – (27)^1/3

= (26.57)^1/3 – 3

or (26.57)^1/3= 3 + △y

Here, dy is approximately equal to △y

dy = (dy/dx)△x

= $\frac{-0.43}{3x^{\frac{2}{3}}}$

= $\frac{-0.43}{3(27)^{\frac{2}{3}}}$

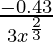
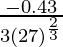
= -0.43/27

Hence, the approximate value of (26.57)^1/3= 3 – 0.43/27 = 2.984

(xiii) (81.5)^1/4

We take y = x^1/4

Let x = 81 and △x = 0.5

△y = (x +△x)^1/4 – x^1/4

= (81.5)^1/4 – (81)^1/4

= (81.5)^1/4 – 3

or (81.5)^1/4= 3 + △y

Here, dy is approximately equal to △y

dy = (dy/dx)△x

= $\frac{0.5}{4x^{\frac{3}{4}}}$

= $\frac{0.5}{4(81)^{\frac{3}{4}}}$

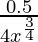
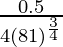
= 0.5/108

Hence, the approximate value of (81.5)^1/4= 3 + 0.5/108 = 3.004

(xiv) (3.968)^3/2

We take y = x^3/2

Let x = 4 and △x = -0.032

△y = (x +△x)^3/2 – x^3/2

= (3.968)^3/2 – (4)^3/2

= (3.968)^3/2 – 8

or (3.968)^3/2= 8 + △y

Here, dy is approximately equal to △y

dy = (dy/dx)△x

= $\frac{(-0.032)(3)\sqrt{x}}{2}$

= $\frac{(-0.032)(3)\sqrt{4}}{2}$

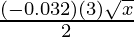
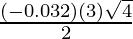
= -0.096

Hence, the approximate value of (3.968)^3/2= 8 – 0.096 = 7.904

(xv) (32.15)^1/5

We take y = x^1/5

Let x = 32 and △x = 0.15

△y = (x +△x)^1/5 – x^1/5

= (32.15)^1/5 – (32)^1/5

= (32.15)^1/5 – 2

or (32.15)^1/5= 2 + △y

Here, dy is approximately equal to △y

dy = (dy/dx)△x

= $\frac{0.15}{5x^{\frac{4}{5}}}$

= $\frac{0.15}{5(32)^{\frac{4}{5}}}$

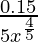
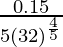
= 0.15/80

Hence, the approximate value of (32.15)^1/5= 2 + 0.15/80 = 2.0018

Question 2. Find the approximate value of f(2.01), where f(x) = 4x²+ 5x + 2.

Solution:

Find the approximate value of f(2.01)

So, f(2.01) = f(2 + 0.01)

x = 2 and △x = 0.01

Given that f(x) = y = 4x²+ 5x + 2 -(1)

On differentiating we get

dy/dx = 8x + 5

dy = (8x + 5)dx = (8x + 5)△x

Now changing x = x + Δx and y = y +Δy in eq(1)

f(x + Δx) = y + Δy

f(2.01) = y + Δy -(2)

f(2 + .01) = y + Δy

since

then Δy = dy and Δx = dx

From eq(2), we get

f(2.01) = (4x²+ 5x + 2) + (8x + 5)△x

= (4(2)²+ 5(2) + 2) + (8(2) + 5)(0.01)

= 16 + 10 + 2 + 0.16 + 0.05

= 28.21

Question 3. Find the approximate value of f(5.001), where f(x) = x³– 7x²+ 15.

Solution:

Find the approximate value of f(5.001)

So, f(5.001) = f(5 + .001)

x = 5 and △x = 0.01,

Given that f(x) = y = x³– 7x²+ 15 -(1)

On differentiating we get

dy/dx = 3x²– 14x

dy = (3x²– 14x) dx = (3x²– 14x) △x

Now changing x = x + Δx and y = y +Δy in eq(1)

f(x + Δx) = y + Δy

f(5.001) = y + Δy -(2)

f(5 + .001) = y + Δy

since

then Δy = dy and Δx = dx

From eq(2), we get

f(5.001) = (x³– 7x²+ 15) + (3x²– 14x) △x

= ((5)³– 7(5)²+ 15) + (3(5)²– 14(5)) (0.001)

= 125 – 175 + 15 + 0.075 + 0.07

= -34.995

Question 4. Find the approximate change in the volume of a cube of side x meters caused by increasing the side by 1%.

Solution:

Volume of cube = x³

V = x³

On differentiating we get

dV/dx = 3x²

Given that Δx = 0.0

dV = 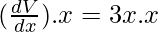$(\frac{dV}{dx}).Δx=3x.Δx$

dV = (3x²)(-0.01x)

= 0.03x³m³

Thus, the approximate change in volume is 0.03x³m³

Question 5.Find the approximate change in the surface area of a cube of side x meters caused by decreasing the side by 1%.

Solution:

Surface area of cube = 6x²

S = 6x²

On differentiating we get

dS/dx = 12x

Given that Δx = -0.01[-ve sign because of decrease]

dS = 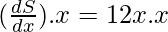$(\frac{dS}{dx}).Δx=12x.Δx$

dS = (12x)(-0.01x)

= -0.12x²m²

Thus, the approximate change in volume is -0.12x²m²

Question 6. If the radius of a sphere is measured as 7m with an error of 0.02m, then find the approximate error in calculating its value.

Solution:

Let r be the radius of the sphere and △r be the error in measuring the radius,

then r = 7m and △r = 0.02m.

Now the volume V of the sphere is given by,

v = 4/3πr²

On differentiating we get

$\frac{dv}{dr}=4πr^2$

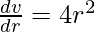
Therefore, dv = (4πr²)Δr = 4π(7)².(0.02)

= 12.30m³

Thus, the approximate error in calculating the volume is 12.30m³

Question 7. If the radius of a sphere is measured as 9m with an error of 0.03m, then find the approximate error in calculating its surface area.

Solution:

Let r be the radius of the sphere and Δr be the error in measuring the radius.

Then r = 9m and Δr = 0.03m.

Now the surface area S of the sphere is given by,

S = 4πr²

On differentiating we get

dS/dr = 8πr

Therefore, dS = (8πr)Δr

= 8π(9).(0.03)

= 2.16πm²

Thus, the approximate error in measuring the surface area is 2.16πm².

Question 8. If f(x) = 3x²+ 15x + 5, then the approximate value of f(3.02) is

(A) 47.66 (B) 57.66 (C)67.66 (D)77.66

Solution:

Given: f(x) = y = 3x²+ 15x + 5 -(1)

f(3.02) = f(3 + 0.2)

So, x = 3 and Δx = 0.02

On differentiating eq(1) we get

f'(x) = y = 6x+ 15

dy = (6x + 15) dx = (6x + 15)Δx

Now changing x = x + Δx and y = y +Δy in eq(1)

f(x + Δx) = y + Δy

f(3.02) = y + Δy -(2)

f(3 + 0.2) = y + Δy

since

then Δy = dy and Δx = dx

From eq(2), we get

f(3.02) = (3x²+ 15x + 5) + (6x + 15)Δx

f(3.02) = (3x²+ 15x + 5) + (6x + 15)(0.02)

= (3(3)²+ 15(3) + 5) + (6(3)+ 15)(0.02)

= 27 + 45 + 5 + 0.36 + 0.3

= 77.66

Hence the correct option is 77.66

Question 9. The approximate change in the volume of a cube of side x meters caused by increasing the side by 3% is

(A) 0.06x³ m³ (B) 0.6x³ m³ (C)0.09x³ m³ (D)0.9x³ m³

Solution:

We have

Volume of cube = v = x³

On differentiating we get

$\frac{dv}{dr}=3x^2$

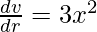
Given that the side increasing 3%, so Δx = 0.03x

$dv=(\frac{dv}{dr}).Δx=3x^2.(0.03x)$

$dv=x^2(0.03x)=0.09x^3m^3$

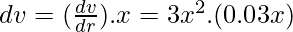
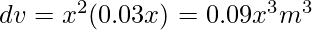
Thus, the approximate change is 0.09x³m³

The correct option is (C)

Whether you're preparing for your first job interview or aiming to upskill in this ever-evolving tech landscape, GeeksforGeeks Courses are your key to success. We provide top-quality content at affordable prices, all geared towards accelerating your growth in a time-bound manner. Join the millions we've already empowered, and we're here to do the same for you. Don't miss out - check it out now!

Last Updated : 05 Mar, 2021

Class 12 NCERT Solutions- Mathematics Part I - Chapter 6 Application of Derivatives -Exercise 6.3 | Set 2

Class 12 NCERT Solutions - Mathematics Part I - Chapter 6 Application of Derivatives - Exercise 6.5 | Set 1

Chapter 1 - Relations and Functions

Chapter 2 - Inverse Trigonometric Functions

Chapter 3 - Matrices

Chapter 4 - Determinants

Chapter 5 - Continuity and Differentiability

Chapter 6 - Applications of Derivatives

Chapter 1 - Relations and Functions

Chapter 2 - Inverse Trigonometric Functions

Chapter 3 - Matrices

Chapter 4 - Determinants

Chapter 5 - Continuity and Differentiability

Chapter 6 - Applications of Derivatives

Class 12 NCERT Solutions- Mathematics Part I – Chapter 6 Application of Derivatives – Exercise 6.4

Question 1. Using differentials, find the approximate value of each of the following up to 3 places of decimal.

Question 2. Find the approximate value of f(2.01), where f(x) = 4x2 + 5x + 2.

Question 3. Find the approximate value of f(5.001), where f(x) = x3 – 7x2 + 15.

Question 4. Find the approximate change in the volume of a cube of side x meters caused by increasing the side by 1%.

Question 5.Find the approximate change in the surface area of a cube of side x meters caused by decreasing the side by 1%.

Question 6. If the radius of a sphere is measured as 7m with an error of 0.02m, then find the approximate error in calculating its value.

Question 7. If the radius of a sphere is measured as 9m with an error of 0.03m, then find the approximate error in calculating its surface area.

Question 8. If f(x) = 3x2 + 15x + 5, then the approximate value of f(3.02) is

(A) 47.66 (B) 57.66 (C)67.66 (D)77.66

Question 9. The approximate change in the volume of a cube of side x meters caused by increasing the side by 3% is

(A) 0.06x3 m3 (B) 0.6x3 m3 (C)0.09x3 m3 (D)0.9x3 m3

Please Login to comment...

Question 2. Find the approximate value of f(2.01), where f(x) = 4x²+ 5x + 2.

Question 3. Find the approximate value of f(5.001), where f(x) = x³– 7x²+ 15.

Question 8. If f(x) = 3x²+ 15x + 5, then the approximate value of f(3.02) is

(A) 0.06x³ m³ (B) 0.6x³ m³ (C)0.09x³ m³ (D)0.9x³ m³