Class 12 NCERT Solutions- Mathematics Part I – Chapter 4 Determinants- Exercise 4.2 | Set 2
Last Updated :
03 Apr, 2024
Note: Please note that Exercise 4.2 from Chapter 4, “Determinants” in the NCERT Solutions, has been removed from the revised syllabus. As a result, this exercise will no longer be a part of your study curriculum.
Question 11. (i)
(ii)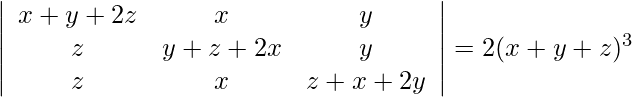
Solution:
(i) L.H.S.=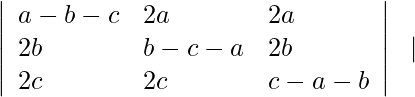
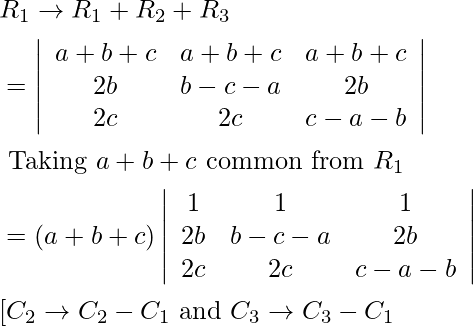

∵ L.H.S.=R.H.S
Hence proved
(ii) 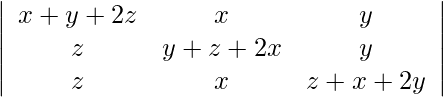
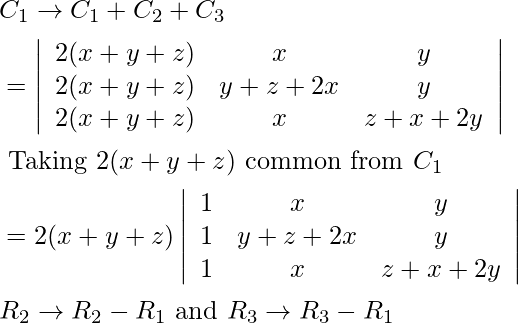
![Rendered by QuickLaTeX.com \begin{array}{l} =2(x+y+z)\left|\begin{array}{ccc} 1 & x & y \\ 0 & x+y+z & 0 \\ 0 & 0 & x+y+z \end{array}\right| \\ =2(x+y+z) \cdot 1 \cdot\left|\begin{array}{cc} x+y+z & 0 \\ 0 & x+y+z \end{array}\right| \\ =2(x+y+z)\left[(x+y+z)^{2}-0\right] \\ =2(x+y+z)^{3} \text { } \end{array}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-45e66ffd9a6a8c56c2d39f5ca5feff50_l3.png)
∵ L.H.S.=R.H.S
Hence proved
Question 12. 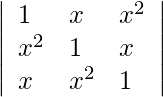
Solution:

![Rendered by QuickLaTeX.com \begin{array}{l} =\left(1+x+x^{2}\right) \cdot 1 \cdot\left|\begin{array}{ll} 1-x^{2} & x-x^{2} \\ x^{2}-x & 1-x \end{array}\right| \\ =\left(1+x+x^{2}\right) \cdot 1 \cdot \mid \begin{array}{ll} (1-x)(1+x) & x(1-x) \\ -x(1-x) & 1-x \end{array} \\ =\left(1+x+x^{2}\right)\left[(1-x)^{2}(1+x)+x^{2}(1-x)^{2}\right] \\ =\left(1+x+x^{2}\right)(1-x)^{2}\left(1+x+x^{2}\right) \\ =\left(1+x+x^{2}\right)^{2}(1-x)^{2} \\ =\left[\left(1+x+x^{2}\right)(1-x)\right]^{2} \\ =\left(1-x+x-x^{2}+x^{2}-x^{2}\right)^{2} \\ =\left(1-x^{3}\right)^{2} \quad \text { } \end{array}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0deb0579240a3f71ba1e00164c76d668_l3.png)
∵ L.H.S.=R.H.S
Hence proved
Question 13. 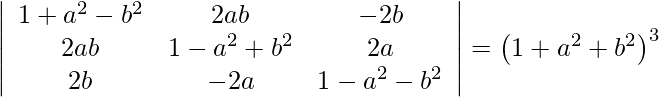
Solution:

![Rendered by QuickLaTeX.com \begin{array}{l} C _{1} \rightarrow C _{1}-b C _{3} \text { and } \left. C _{2} \rightarrow C _{2}+ aC _{3}\right] \\ =\begin{array}{ccc} \left|\begin{array}{lll} 1+a^{2}+b^{2} & 0 & -2 b \\ 0 & 1+a^{2}+b^{2} & 2 a \\ b\left(1+a^{2}+b^{2}\right) & -a\left(1+a^{2}+b^{2}\right) & 1-a^{2}-b^{2} \end{array}\right| \end{array} \\ =\left(1+a^{2}+b^{2}\right)\left|\begin{array}{ccc} 1 & 0 & -2 b \\ 0 & 1 & 2 a \\ b & -a & 1-a^{2}-b^{2} \end{array}\right| \\ {\left[ R _{1} \rightarrow R _{1}-bR_{1} \right]} \end{array}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-86af6b35ea1198e5b375480f9fc49da7_l3.png)
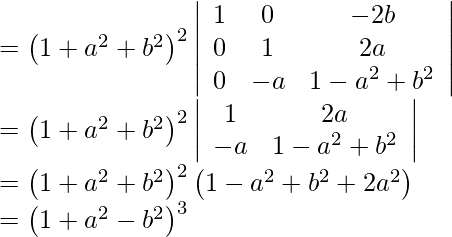
∵ L.H.S.=R.H.S
Hence proved
Question 14. 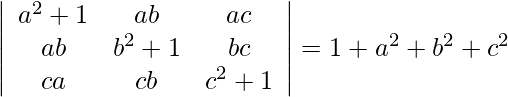
Solution:
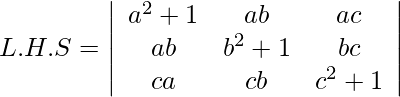
Multiplying column1,column2,column3 by a,b,c respectively and then dividing the determinant by a,b,c .
![Rendered by QuickLaTeX.com \begin{aligned} &=\frac{1}{a b c}\left|\begin{array}{ccc} a\left(a^{2}+1\right) & a b^{2} & a c^{2} \\ a^{2} b & b\left(b^{2}+1\right) & b c^{2} \\ a^{2} c & b^{2} c & c\left(c^{2}+1\right) \end{array}\right|\\ &\text { Taking a } b \text { and } c \text { common from } R_{1}, R_{2} \text { and } R_{3} \text { respectively }\\ &=\frac{a b c}{a b c} \begin{array}{ccc} =\left|\begin{array}{lll} a^{2}+1 & b^{2} & c^{2} \\ a^{2} & b^{2}+1 & c^{2} \\ a^{2} & b^{2} & c^{2}+1 \end{array}\right| \end{array}\\ &\left[ C _{1} \rightarrow C _{1}- C _{2}+ C _{3}\right]\\ &=\frac{a b c}{a b c}\left|\begin{array}{ccc} 1+a^{2}+b^{2}+c^{2} & b^{2} & c^{2} \\ 1+a^{2}+b^{2}+c^{2} & b^{2}-1 & c^{2} \\ 1-a^{2}+b^{2}-c^{2} & b^{2} & c^{2}+1 \end{array}\right| \end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e5f21f25ac4acf0f67777d828fe12124_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned} &=\left(1+a^{2}+b^{2}+c^{2}\right)\left|\begin{array}{ccc} 1 & b^{2} & c^{2} \\ 1 & b^{2}+1 & c^{2} \\ 1 & b^{2} & c^{2}+1 \end{array}\right|\\ &\left[ R _{2} \rightarrow R _{2}- R _{1} \text { and } R _{3} \rightarrow R _{3}- R _{1}\right]\\ &=\left(1+a^{2}+b^{2}+c^{2}\right)\left|\begin{array}{ccc} 1 & b^{2} & c^{2} \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right|\\ &=\left(1+a^{2}+b^{2}+c^{2}\right)(1)(1-0)\\ &=1+a^{2}+b^{2}+c^{2}\\ &\text { } \end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bf0af8839314e8b3ffbc9f2fe1b8ff50_l3.png)
∵ L.H.S.=R.H.S
Hence proved
Choose the correct answer in Exercises 15 and 16.
Question 15. Let A be a square matrix of order 3 x 3, then|A| is equal to:
(A) k|A|
(B) k2|A|
(C) k3|A|
(D) 3k|A|
Solution:
Let A =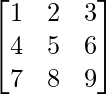 be a square matrix of order 3 x 3 ….(1)
be a square matrix of order 3 x 3 ….(1)
Now, kA=
⇒|kA|=
⇒|kA|=k3 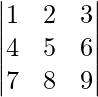
∴ |kA|= k3|A| [ from eqn .(1) ]
∴ option (C) is correct.
Question 16.Which of the following is correct
(A) Determinant is a square matrix.
(B) Determinant is a number associated to a matrix.
(C) Determinant is a number associated to a square matrix.
(D) None of these
Solution:
Since, Determinant is a number which is always associated to a square matrix.
∴ option (C) is correct.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...