Question 1. Solve the following of equation graphically
x + y = 3
2x + 5y = 12
Solution:
Given that, 2x + 5y = 12 and x + y = 3
We have,
x + y = 3,
When y = 0, we get x = 3
When x = 0, we get y = 3
So, the following table giving points on the line x + y = 3:
Now, 2 + 5y = 12
y = (12 – 2x)/5
When x = 1, we have
y = (12 – 2)/5 = 4
When x = -4, we have
y = (12 – 2(-4))/5 = 4
So, the following table giving points on the line 2x + 5y = 12:
So, the graph of the equation x + y = 3 and 2x + 5y = 12 is
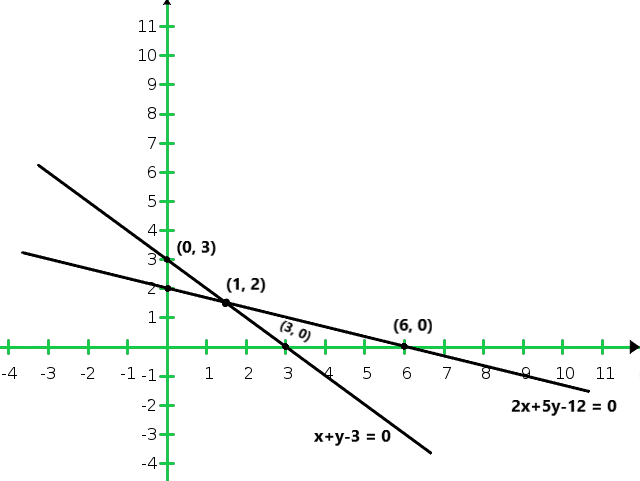
From the graph we conclude that the two lines intersect at a point P (1, 2).
Hence x = 1 and y = 2 are required point.
Question 2. Solve the following of equation graphically
x – 2y = 5
2x + 3y = 10
Solution :
Given that,, x – 2y = 5 and 2x + 3y = 10
Now, x – 2y = 5
x = 5 + 2y
When y = 0, we get x = 5
When y = -2, we get x = 1
So, the following table giving points on the line x – 2y = 5
Now, 2x + 3y = 10
x = (10 – 3y)/2
When y = 0, we get x = 5
When y = 2, we get x = 2
So, the following table giving points on the line 2x + 3y = 10
So, the graph of the equation x – 2y = 5 and 2x + 3y = 10
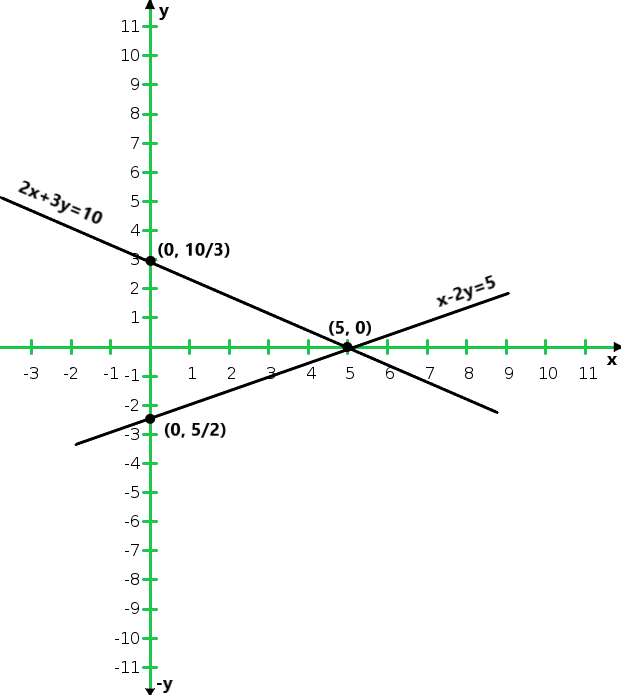
From the graph we conclude that the two lines intersect at a point P (5, 0)
Hence x = 5 and y = 0 are required point.
Question 3. Solve the following of equation graphically
3x + y + 1 = 0
2x – 3y + 8 = 0
Solution:
Given that, 3x + y + 1 = 0 and 2x – 3y + 8 = 0
Now 3x + y + 1 = 0
y = -1 – 3x
When x = 0, we get x = -1
When y = -1, we get x = 2
So, the following table giving points on the line x – 2y = 5
Now, 2x – 3y + 8 = 0
x = (3y – 8)/2
When y = 0, we get x = -4
When y = 2, we get x = 1
So, the following table giving points on the line 2x + 3y = 10
So, the graph of the equation 3x + y + 1 = 0 and 2x – 3y + 8 = 0
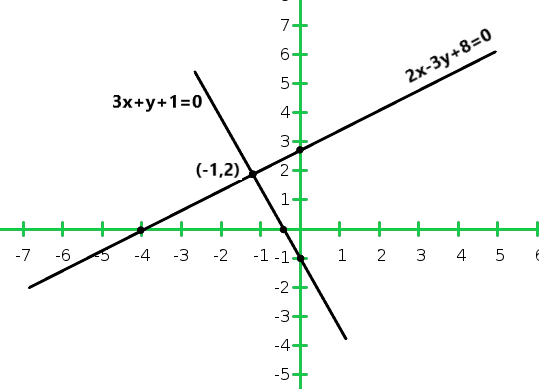
From the graph we conclude that the two lines intersect at a point P (-1, 2)
Hence x = -1 and y = 2 are required points.
Question 4. Solve the following of equation graphically
2x + y – 3 = 0
2x – 3y – 7 = 0
Solution:
Given that,, 2x + y – 3 = 0 and 2x – 3y – 7 = 0
Now 2x + y – 3 = 0,
y = 3 – 2x
When x = 0, we get x = 3
When x = 1, we get x = 1
So, the following table giving points on the line 2x + y – 3 = 0
Now, 2x – 3y – 7 = 0
When x = 0, we get y = 1
When x = 2, we get y = -1
So, the following table giving points on the line 2x + 3y = 10
So, the graph of the equation 2x + y – 3 = 0 and 2x – 3y – 7 = 0
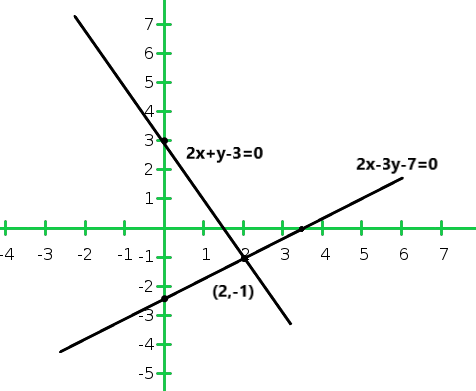
From the graph we conclude that the two lines intersect at a point P (2,-1)
Hence x = 2 and y = -1 are required points.
Question 5. Solve the following of equation graphically
x + y = 6
x – y = 2
Solution:
Given that, x + y = 6 and x – y = 2
Now x + y = 6
y = 6 – x
When x = 2, we get y = 4
When x = 3, we get y = 3
So, the following table giving points on the line x + y = 6
Now , x – y = 2
y = x – 2
When x = 0, we get y = – 2
When x = 2, we get y = 0
So, the following table giving points on the line x – y = 2
So, the graph of the equation x + y = 6 and x – y = 2
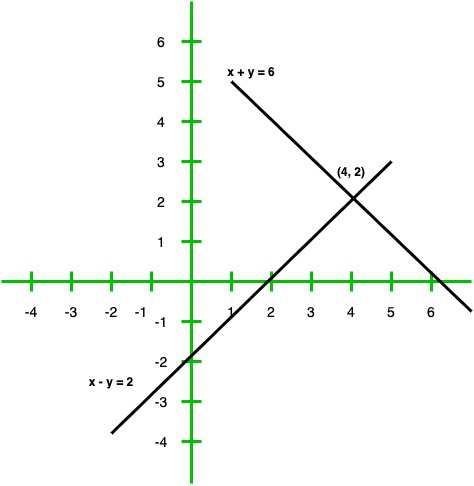
From the graph we conclude that the two lines intersect at a point P (4, 2)
Hence x = 4 and y = 2 are required points.
Question 6. Solve the following of equation graphically
x – 2y = 6
3x – 6y = 0
Solution:
Given that, x – 2y = 6 and 3x – 6y = 0
Now x – 2y = 6
x = 6 + 2y
When y = -2, we get x = 2
When y = -3, we get x = 0
So, the following table giving points on the line x – 2y = 6
Now, 3x – 6y = 0
= x = 2y
When y = 0, we get y = 0
When y = -1, we get x = 2
So, the following table giving points on the line 3x – 6y = 0
So, the graph of the equation x – 2y = 6 and 3x – 6y = 0
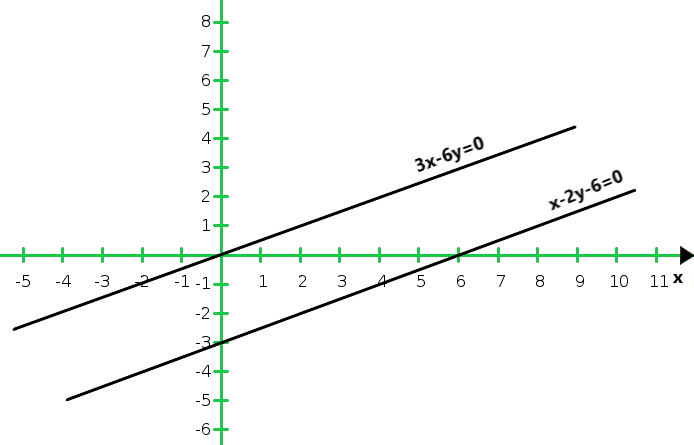
From the graph we conclude that the two lines are parallel to each other so, the two lines have no common point.
Hence the given system has no solutions.
Question 7. Solve the following of equation graphically
x + y = 4
2x – 3y = 3
Solution:
Given that, x + y = 4 and 2x – 3y = 3
Now x + y = 4
x = 4 – y
When y = 0, we get x = 4
When y = 2, we get x = 2
So, the following table giving points on the line x + y = 4
Now , 2x – 3y = 3
x = (3y + 3)/2
When y = 1, we get x = 3
When y = -1, we get x = 0
So, the following table giving points on the line 2x – 3y = 3
So, the graph of the equation x + y = 4 and 2x – 3y = 3
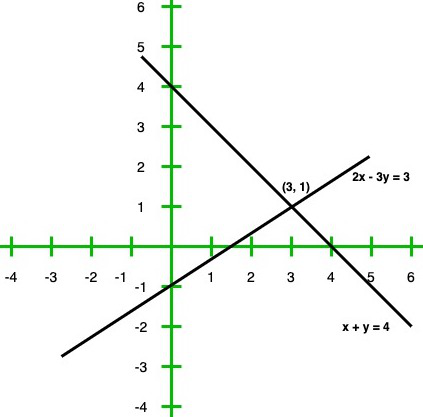
From the graph we conclude that the two lines intersect at a point P(3, 1)
Hence x = 3 and y = 1 are required points.
Question 8. Solve the following of equation graphically
2x + 3y = 4
x – y + 3 = 0
Solution:
Given that, 2x + 3y = 4 and x – y + 3 = 0
Now 2x + 3y = 4
x = (4 – 3y)/2
When y = 0, we get x = 2
When y = 2, we get x = – 1
So, the following table giving points on the line x + y = 4
Now, x – y + 3 = 0
x = y – 3
When y = 3, we get x = 0
When y = 4, we get x = 1
So, the following table giving points on the line x – y + 3 = 0
So, the graph of the equation 2x + 3y = 4 and x – y + 3 = 0
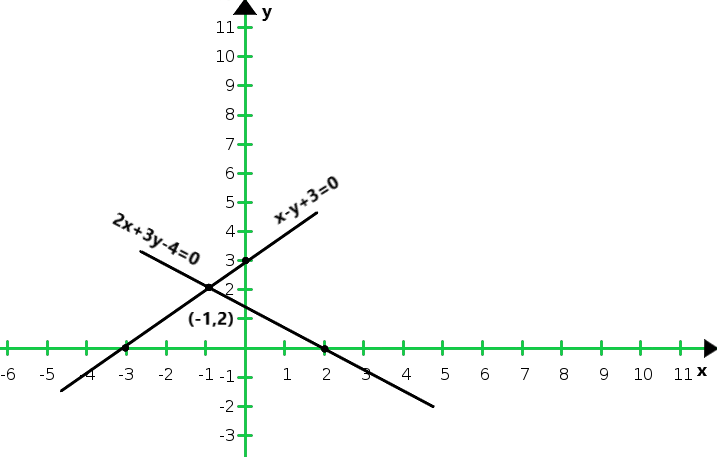
From the graph we conclude that the two lines intersect at (-1, 2)
Hence x = -1 and y = 2 are required points.
Question 9. Solve the following of equation graphically
2x – 3y + 13 = 0
3x – 2y + 12 = 0
Solution:
Given that, 2x – 3y + 13 = 0 and 3x – 2y + 12 = 0
Now, 2x – 3y + 13 = 0
x = (3y – 13)/2
When y = 1, we get x = – 5
When y = 3, we get x = – 2
So, the following table giving points on the line 2x – 3y + 13 = 0
Now, 3x – 2y + 12 = 0
x = (2y – 12)/3
When y = 0, we get x = -14
When y = 3, we get x = -2
So, the following table giving points on the line x – y + 3 = 0
So, the graph of the equation 2x – 3y + 14 = 0 and 3x – 2y + 12 = 0
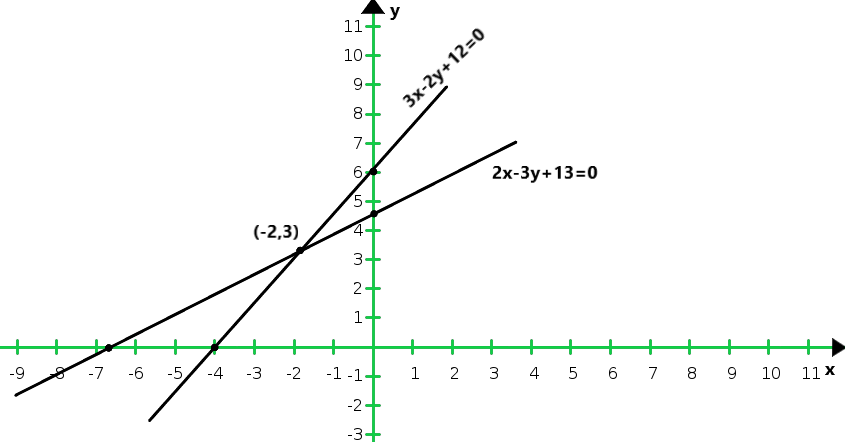
From the graph we conclude that the two lines intersect at (- 2, 3)
Hence x = – 2 and y = 3 are required points.
Question: 10. Solve the following of equation graphically
2x + 3y + 5 = 0
3x – 2y – 12 = 0
Solution:
Given that, 2x + 3y + 5 = 0 and 3x – 2y – 12 = 0
Now, 2x + 3y + 5 = 0,
x = (-3y – 5)/2
When y = 1, we get x = – 4
When y = -1, we get x = -1
So, the following table giving points on the line 2x + 3y + 5 = 0
Now, 3x – 2y – 12 = 0,
x = (2y + 12)/3
When y = 0, we get x = 4
When y = 3, we get x = 6
So, the following table giving points on the line 3x – 2y – 12 = 0
So, the graph of the equation 2x + 3y + 5 = 0 and 3x – 2y – 12 = 0
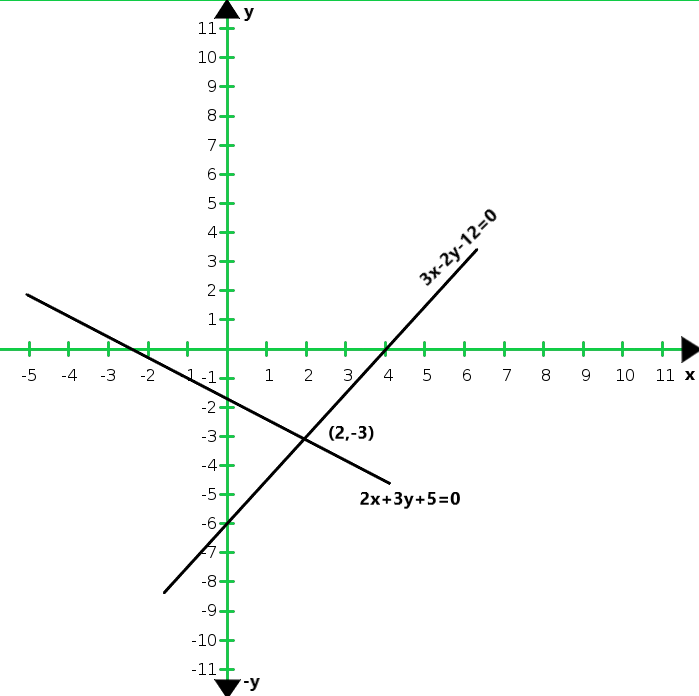
From the graph we conclude that the two lines intersect at (2, 3).
Hence x = 2 and y = 3 are required points.
Question 11. Solve the following of equation graphically
2x + 3y = 6
4x + 6y = 12
Solution:
Given that, 2x + 3y = 6 and 4x + 6y = 12
Now, 2x + 3y = 5
x = (6-3y)/2
When y = 0, we get x = 3
When y = 2, we get x = 0
So, the following table giving points on the line 2x + 3y = 6
Now, 4x + 6y = 12
x = (12 – 6y)/4
When y = 0, we get x = 3
When y = 2, we get x = 0
So, the following table giving points on the line 4x + 6y = 12
So, the graph of the equation 2x + 3y = 6 and 4x + 6y = 12
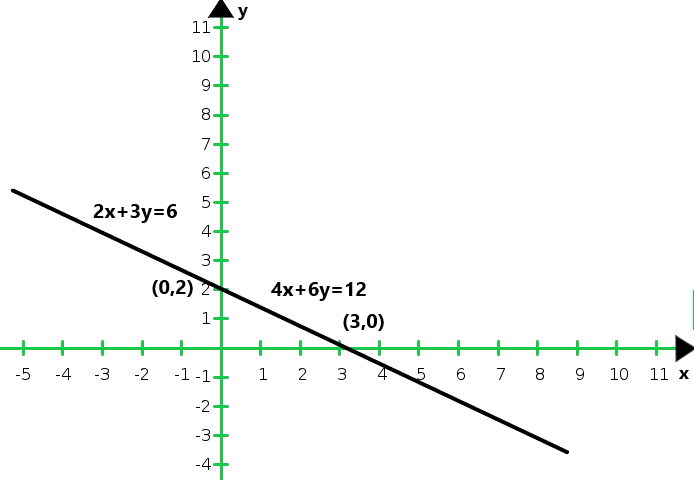
From the graph we conclude that the two equations are coincident.
Hence, the system of equations has infinitely many solutions.
Question 12. Solve the following of equation graphically
x – 2y = 5
3x – 6y = 15
Solution:
Given that, x – 2y = 5 and 3x – 6y = 15
Now, x – 2y = 5
x = 2y + 5
When y = -1, we get x = 3
When y = 0, we get x = 5
So, the following table giving points on the line x – 2y = 5
Now, 3x – 6y = 15
x = (15 + 6y)/3
When y = -2, we get x = 1
When y = -3, we get x = -1
So, the following table giving points on the line 3x – 6y = 15
So, the graph of the equations x – 2y = 5 and 3x – 6y = 15:
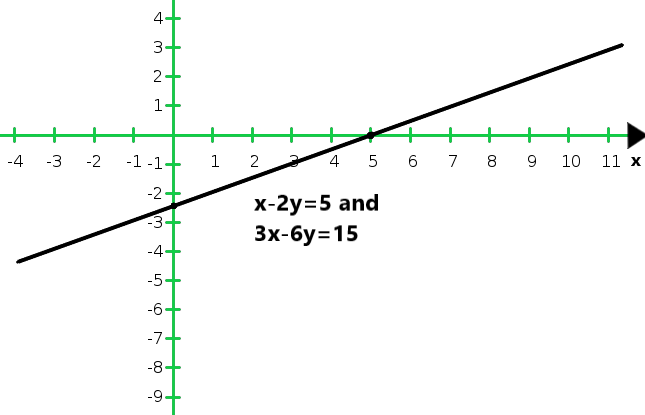
From the graph we conclude that the two equations are coincident.
Hence, the system of equations has infinitely many solutions.
Question 13. Solve the following of equation graphically
3x + y = 8
6x + 2y = 16
Solution:
Given that, 3x + y = 8 and 6x + 2y = 16
Now, x – 2y = 5
= y = 8 – 3x
When x = 2, we get y = 2
When x = 3, we get y = -1
So, the following table giving points on the line 3x + y = 8
Now, 6x + 2y = 16
y = (16 – 6x)/2
When x = 1, we get y = 5
When x = 3, we get y = -1
So, the following table giving points on the line 6x + 2y = 16
So, the graph of the given equations 3x + y = 8 and 6x + 2y = 16:
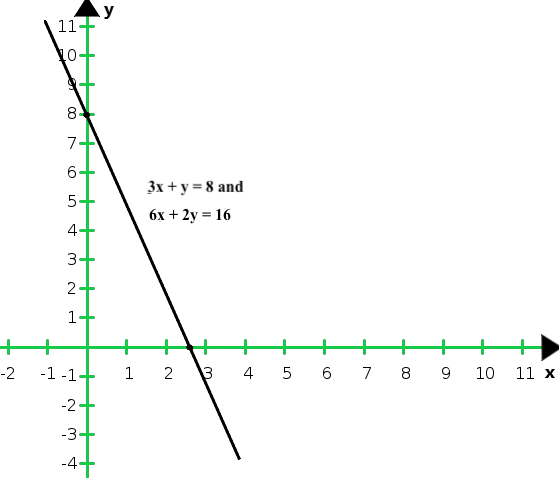
From the graph we conclude that the graphs of the two equations are coincident
Hence, the system of equations has infinitely many solutions.
Share your thoughts in the comments
Please Login to comment...