Class 10 RD Sharma Solutions – Chapter 13 Probability – Exercise 13.2
Last Updated :
18 Mar, 2021
Question 1. Suppose you drop a tie at random on the rectangular region shown in fig. below. What is the probability that it will land inside the circle with diameter 1 m?

Solution:
Area of a circle with the specified radius 0.5 m = (0.5)2 = 0.25 πm2
Area of the rectangle = length × breadth = 3 × 2 = 6m2
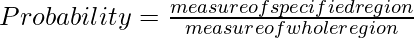
Now,
The probability that the tie will land inside the circle, = area of circle/area of rectangle
= 0.25 π m2 / 6 m2
= π /24
Therefore, the probability that the tie will land inside the circle = π/24
Question 2. In the accompanying diagram, a fair spinner is placed at the centre O of the circle. Diameter AOB and radius OC divide the circle into three regions labelled X, Y and Z.? If ∠BOC = 45°. What is the probability that the spinner will land in the region X?

Solution:
Given,
∠BOC = 45°
Also, by the application of linear pair
∠AOC = 180 – 45 = 135°
Area of circle of radius r = πr2
Area of region x according to the figure= θ/360 × πr2
= 135/360 × πr2
= 3/8 × πr2
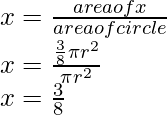
Hence, The required probability that the spinner will land in the region X is 3/8.
Question 3. A target is shown in fig. below consists of three concentric circles of radii, 3, 7 and 9 cm respectively. A dart is thrown and lands on the target. What is the probability that the dart will land on the shaded region?

Solution:
Now, we have the following values
I circle – with radius 3
II circle – with radius 7
III circle – with radius 9
Their corresponding areas are :
Area of I circle = π(3)2 = 9π
Area of II circle = π(7)2 = 49π
Area of III circle = π(9)2 = 81π
Now, calculating,
Area of shaded region = Area of II circle – Area of I circle
= 49π − 9π
= 40π
Now, the probability that it will land on the shaded region is given by,

Hence, the required probability that the dart will land on the shaded region is equivalent to 40/81.
Question 4. In the figure, points A, B, C and D arc the centres of four circles that each have a radius of length one unit. If a point is selected at random from the interior o’ square ABCD. What is the probability that the point will be chosen from the shaded region?

Solution:
Radius of each of the circles = 1 unit
Therefore,
side of the square ABCD = 2 units
Area of sq ABCD = side2 = a2 = 2 * 2 = 4 sq. units
Also,
Area of four quadrants at A,B,C and D is given by
= 4 * 1/4 πr2
Substituting the values of r , we get,
= π sq. unit
Therefore, area of shaded region = (4 – π) sq. units
And, the probability of the point that is selected from the shaded region = (4 – π)/4 = (1 – π/4)
Question 5. In the figure, JKLM is a square with sides of length 6 units. Points A and B are the mid-points of sides KL and LM respectively. If a point is selected at random from the interior of the square. What is the probability that the point will be chosen from the interior of ∆JAB?

Solution:
We know,
Length of sq side of JKLM = 6 units
Now, the area of the sq. JKLM = 62 = 36 sq. units
We have, A and B as the midpoints of sides KL and LM.
Now,
AL = AK = BM = BL = 3 units
Therefore,
Area of triangle AJK = (JK * AK) /2 = (6 * 3) / 2 = 9 sq. units
Area of triangle JMB = (JM * MB) /2 = (6 * 3) / 2 = 9 sq. units
Area of triangle LAB = (LA * LB) /2 = (3 * 3) / 2 = 9/2 sq. units
Sum of these areas = 9 + 9 + 9/2 = 45/2 sq units.
Area of triangle JAB = Area of sq JKLM – Area of all the three triangles
= 36 – 45/2 = 72-45/2 sq. units
= 27/2 sq. units
Probability = Area of triangle JAB/ Area of sq JMLK
= 27 /(2 * 36) = 3/8
Question 6. In the figure, a square dart board is shown. The length of a side of the larger square is 1.5 times the length of a side of the smaller square. If a dart is thrown and lands on the larger square. What is the probability that it will land in the interior of the smaller square?

Solution:
Let us assume the side of the smaller sq to be a.
Also, let the length of the side of sq ABCD be 3/2 * a
Area of the sq. ABCD = (3a/2)2 = 9/4 a2 sq. units
Therefore,
Probability = 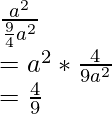
Share your thoughts in the comments
Please Login to comment...