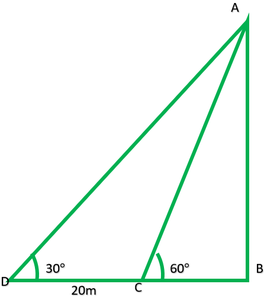
Question 11. A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30° (see Fig.). Find the height of the tower and the width of the canal.
Solution:
In fig: AB = tower = ?
CB = canal = ?
In rt. ∆ABC,
tan60° = 
h/x = √3
h = √3 x -(1)
In rt. ∆ABD
= tan 30°
= 1/√3
h = (x + 20)/√3 -(2)
From (1) and (2)
√3/1 = (x + 20)/√3
3x = x + 20
3x – x = 20
2x = 20
X = 20/2
X = 10
Width of the canal is 10m
Putting value of x in equation 1
h = √3 x
= 1.732(10)
= 17.32
Height of the tower 17.32m.
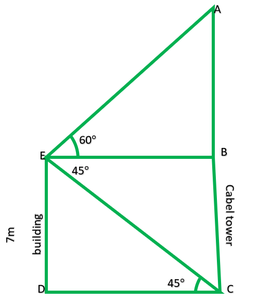
Question 12. From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
Solution:
In fig: ED = building = 7m
AC = cable tower = ?
In rt ∆EDC,
= tan45°
7/x = 1/1
DC = 7
Now, EB = DC = 7m
In rt. ∆ABE,
= tan60°
AB/7 = √3/1
Height of tower = AC = AB + BC
7√3 + 7
= 7(√3 + 1)
= 7(1.732 + 1)
= 7(2.732)
Height of cable tower = 19.125m
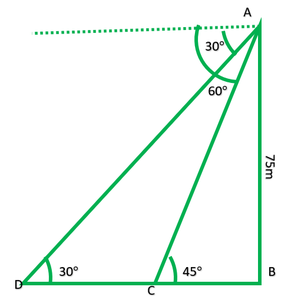
Question 13. As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
Solution:
In fig:
AB = lighthouse = 75m
D and C are two ships
DC = ?
In rt. ∆ABD,
= tan30°
75/BD = 1/√3
BD = 75√3
In rt. ∆ABC
= tan45°
75/BC = 1/1
BC = 75
DC = BD – BC
= 75√3 – 75
75(√3 – 1)
75(1.372 – 1)
34.900
Hence, distance between two sheep is 34.900
Question 14. A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After some time, the angle of elevation reduces to 30° (see Fig.). Find the distance traveled by the balloon during the interval.
Solution:
In fig: AB = AC – BC
= 88.2 – 1.2
= 81m
In rt. ∆ABE
= 87/EB = tan30°
87/EB = 1/√3
EB = 87√3
In rt. ∆FDE
= tan60°
√3 ED = 87
ED = 87/√3
DB = DB – ED
87√3 – 87/√3
87(√3 – 1/√3)
= 87(3 – 1/√3)
= 87(2/√3) = 174/√3 * √3/√3
= 174 * √3/3 = 58√3
58 * 1.732 = 100.456m
Distance traveled by balloon is 100.456m
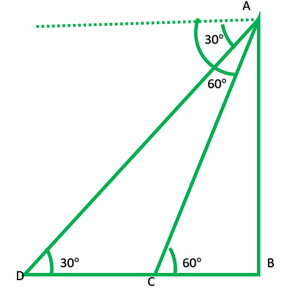
Question 15. A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.
Solution:
In fig: AB is tower
In rt. ∆ABD
= tan30°
= 1/√3
DB = √3 AB -(1)
In rt. ∆ABC
= tan60°
BC = AB/√3 -(2)
DC = DB – BC
= √3 AB – AB/√3
AB(3 – 1/√3)
CD = 2AB/√3
S1 = S2
\frac{D1}{T1} = \frac{D2}{T2}
2/√3AB/6 = AB/√3/t
2t = 6
t = 6/2
t = 3sec
Question 16. The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
Solution:
In fig: AB is tower
To prove: AB = 6m
Given: BC = 4m DB = 9m
In ∆ABC
= tanθ
AB/4 = tanθ -(1)
In ∆ABD
= tan (90°-θ)
AB/9 = 1/ tanθ
9/AB = tanθ -(2)
From (1) and (2)
AB/4 = 9/AB
AB2 = 36
AB = √36
AB = √(6 * 6)
AB = 6m
Height of the tower is 6m.
