Serialize and Deserialize a Binary Tree
Last Updated :
20 Feb, 2023
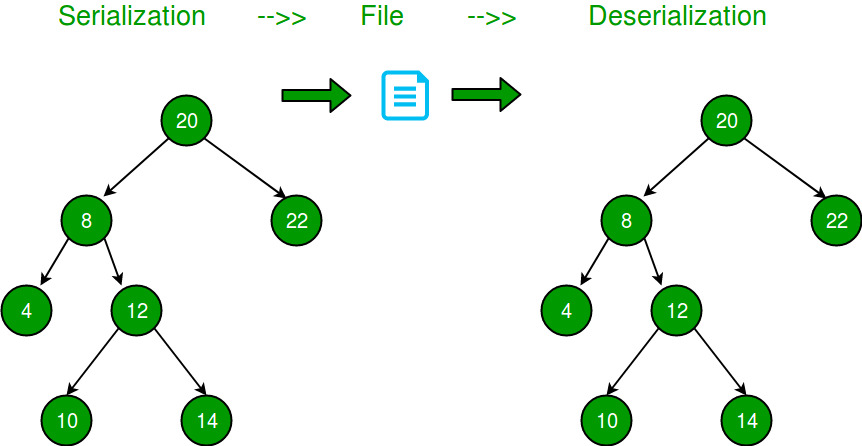
Serialization is to store the tree in a file so that it can be later restored. The structure of the tree must be maintained. Deserialization is reading the tree back from a file.
Following are some simpler versions of the problem:
If given Tree is a Binary Search Tree?
If the given Binary Tree is Binary Search Tree, we can store it by either storing preorder or postorder traversal. In case of Binary Search Trees, only preorder or postorder traversal is sufficient to store structure information.
If given Binary Tree is Complete Tree?
A Binary Tree is complete if all levels are completely filled except possibly the last level and all nodes of last level are as left as possible (Binary Heaps are complete Binary Tree). For a complete Binary Tree, level order traversal is sufficient to store the tree. We know that the first node is root, next two nodes are nodes of next level, next four nodes are nodes of 2nd level and so on.
If given Binary Tree is Full Tree?
A full Binary is a Binary Tree where every node has either 0 or 2 children. It is easy to serialize such trees as every internal node has 2 children. We can simply store preorder traversal and store a bit with every node to indicate whether the node is an internal node or a leaf node.
How to store a general Binary Tree?
A simple solution is to store both Inorder and Preorder traversals.
This solution requires space twice the size of the Binary Tree. We can save space by storing Preorder traversal and a marker for NULL pointers.
- Store all possible child nodes for each node.
- If there is no child node then push -1 for that child.
- Put this preorder traversal in the file.
Examples:
Input:
12
/
13
Output: 12 13 -1 -1 -1
Input:
20
/ \
8 22
Output: 20 8 -1 -1 22 -1 -1
Input:
20
/
8
/ \
4 12
/ \
10 14
Output: 20 8 4 -1 -1 12 10 -1 -1 14 -1 -1 -1
Input:
20
/
8
/
10
/
5
Output: 20 8 10 5 -1 -1 -1 -1 -1
Input:
20
\
8
\
10
\
5
Output: 20 -1 8 -1 10 -1 5 -1 -1
How to deserialize the above serialization?
Deserialization can be done by simply reading data from the file one by one and keep on adding children till a -1 is reached. If both the children are NULL then return back to the parent.
Below is the implementation of the above idea.
C++
#include <bits/stdc++.h>
using namespace std;
#define MARKER -1
struct Node {
int key;
struct Node *left, *right;
};
struct Node* newNode(int key)
{
struct Node* temp = new Node();
temp->key = key;
temp->left = temp->right = NULL;
return (temp);
}
void serialize(Node* root, FILE* fp)
{
if (root == NULL) {
fprintf(fp, "%d ", MARKER);
return;
}
fprintf(fp, "%d ", root->key);
serialize(root->left, fp);
serialize(root->right, fp);
}
void deSerialize(Node*& root, FILE* fp)
{
int val;
if (!fscanf(fp, "%d ", &val) || val == MARKER)
return;
root = newNode(val);
deSerialize(root->left, fp);
deSerialize(root->right, fp);
}
void inorder(Node* root)
{
if (root) {
inorder(root->left);
printf("%d ", root->key);
inorder(root->right);
}
}
int main()
{
struct Node* root = newNode(20);
root->left = newNode(8);
root->right = newNode(22);
root->left->left = newNode(4);
root->left->right = newNode(12);
root->left->right->left = newNode(10);
root->left->right->right = newNode(14);
FILE* fp = fopen("tree.txt", "w");
if (fp == NULL) {
puts("Could not open file");
return 0;
}
serialize(root, fp);
fclose(fp);
Node* root1 = NULL;
fp = fopen("tree.txt", "r");
deSerialize(root1, fp);
printf("Inorder Traversal of the tree constructed from "
"file:\n");
inorder(root1);
return 0;
}
|
Java
import java.util.*;
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) { val = x; }
}
class BinaryTree {
TreeNode root;
public static String serialize(TreeNode root)
{
if (root == null) {
return null;
}
Stack<TreeNode> s = new Stack<>();
s.push(root);
List<String> l = new ArrayList<>();
while (!s.isEmpty()) {
TreeNode t = s.pop();
if (t == null) {
l.add("#");
}
else {
l.add("" + t.val);
s.push(t.right);
s.push(t.left);
}
}
return String.join(",", l);
}
static int t;
public static TreeNode deserialize(String data)
{
if (data == null)
return null;
t = 0;
String[] arr = data.split(",");
return helper(arr);
}
public static TreeNode helper(String[] arr)
{
if (arr[t].equals("#"))
return null;
TreeNode root
= new TreeNode(Integer.parseInt(arr[t]));
t++;
root.left = helper(arr);
t++;
root.right = helper(arr);
return root;
}
static void inorder(TreeNode root)
{
if (root != null) {
inorder(root.left);
System.out.print(root.val + " ");
inorder(root.right);
}
}
public static void main(String args[])
{
BinaryTree tree = new BinaryTree();
tree.root = new TreeNode(20);
tree.root.left = new TreeNode(8);
tree.root.right = new TreeNode(22);
tree.root.left.left = new TreeNode(4);
tree.root.left.right = new TreeNode(12);
tree.root.left.right.left = new TreeNode(10);
tree.root.left.right.right = new TreeNode(14);
String serialized = serialize(tree.root);
System.out.println("Serialized view of the tree:");
System.out.println(serialized);
System.out.println();
TreeNode t = deserialize(serialized);
System.out.println(
"Inorder Traversal of the tree constructed"
+ " from serialized String:");
inorder(t);
}
}
|
C#
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
class TreeNode {
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode(int x) { val = x; }
}
class BinaryTree {
public TreeNode root;
public static string Serialize(TreeNode root)
{
if (root == null) {
return null;
}
Stack<TreeNode> s = new Stack<TreeNode>();
s.Push(root);
List<string> l = new List<string>();
while (s.Count > 0) {
TreeNode t = s.Pop();
if (t == null) {
l.Add("#");
}
else {
l.Add(t.val.ToString());
s.Push(t.right);
s.Push(t.left);
}
}
return string.Join(",", l);
}
static int t;
public static TreeNode Deserialize(string data)
{
if (data == null)
return null;
t = 0;
string[] arr = data.Split(',');
return Helper(arr);
}
public static TreeNode Helper(string[] arr)
{
if (arr[t].Equals("#"))
return null;
TreeNode root = new TreeNode(int.Parse(arr[t]));
t++;
root.left = Helper(arr);
t++;
root.right = Helper(arr);
return root;
}
static void Inorder(TreeNode root)
{
if (root != null) {
Inorder(root.left);
Console.Write(root.val + " ");
Inorder(root.right);
}
}
public static void Main(string[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new TreeNode(20);
tree.root.left = new TreeNode(8);
tree.root.right = new TreeNode(22);
tree.root.left.left = new TreeNode(4);
tree.root.left.right = new TreeNode(12);
tree.root.left.right.left = new TreeNode(10);
tree.root.left.right.right = new TreeNode(14);
string serialized = Serialize(tree.root);
Console.WriteLine("Serialized view of the tree:");
Console.WriteLine(serialized);
Console.WriteLine();
TreeNode t = Deserialize(serialized);
Console.WriteLine(
"Inorder Traversal of the tree constructed"
+ " from serialized String:");
Inorder(t);
}
}
|
Javascript
const MARKER = -1;
class Node {
constructor(key) {
this.key = key;
this.left = null;
this.right = null;
}
}
function newNode(key) {
let temp = new Node(key);
return temp;
}
function serialize(root, fp) {
if (root === null) {
fp.push(MARKER);
return;
}
fp.push(root.key);
serialize(root.left, fp);
serialize(root.right, fp);
}
function deSerialize(root, fp) {
let val = fp.shift();
if (val === undefined || val === MARKER) {
return null;
}
root = newNode(val);
root.left = deSerialize(root.left, fp);
root.right = deSerialize(root.right, fp);
return root;
}
function inorder(root) {
if (root) {
inorder(root.left);
console.log(root.key);
inorder(root.right);
}
}
function main() {
let root = newNode(20);
root.left = newNode(8);
root.right = newNode(22);
root.left.left = newNode(4);
root.left.right = newNode(12);
root.left.right.left = newNode(10);
root.left.right.right = newNode(14);
let fp = [];
serialize(root, fp);
let root1 = null;
root1 = deSerialize(root1, fp);
console.log("Inorder Traversal of the tree constructed from file:");
inorder(root1);
return 0;
}
main();
|
Python3
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
class BinaryTree:
def __init__(self):
self.root = None
def serialize(self, root):
if not root:
return None
stack = [root]
l = []
while stack:
t = stack.pop()
if not t:
l.append("#")
else:
l.append(str(t.val))
stack.append(t.right)
stack.append(t.left)
return ",".join(l)
def deserialize(self, data):
if not data:
return None
global t
t = 0
arr = data.split(",")
return self.helper(arr)
def helper(self, arr):
global t
if arr[t] == "#":
return None
root = TreeNode(int(arr[t]))
t += 1
root.left = self.helper(arr)
t += 1
root.right = self.helper(arr)
return root
def inorder(self, root):
if root:
self.inorder(root.left)
print(root.val, end=" ")
self.inorder(root.right)
if __name__ == '__main__':
tree = BinaryTree()
tree.root = TreeNode(20)
tree.root.left = TreeNode(8)
tree.root.right = TreeNode(22)
tree.root.left.left = TreeNode(4)
tree.root.left.right = TreeNode(12)
tree.root.left.right.left = TreeNode(10)
tree.root.left.right.right = TreeNode(14)
serialized = tree.serialize(tree.root)
print("Serialized view of the tree:")
print(serialized)
print()
t = tree.deserialize(serialized)
print("Inorder Traversal of the tree constructed from serialized String:")
tree.inorder(t)
|
How much extra space is required in above solution?
If there are n keys, then the above solution requires n+1 markers which may be better than simple solution (storing keys twice) in situations where keys are big or keys have big data items associated with them.
Can we optimize it further?
The above solution can be optimized in many ways. If we take a closer look at the above serialized trees, we can observe that all leaf nodes require two markers. One simple optimization is to
- Store a separate bit with every node to indicate that the node is internal or external.
- This way we don’t have to store two markers with every leaf node as leaves can be identified by the extra bit.
- We still need a marker for internal nodes with one child.
For example, in the following diagram, the character ‘ is used to indicate an internal node set bit, and ‘/‘ is used as NULL marker.
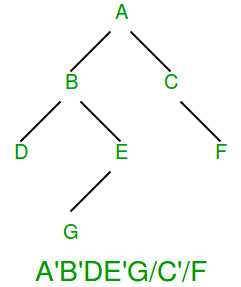
Please note that there are always more leaf nodes than internal nodes in a Binary Tree (Number of the leaf nodes is the number of internal nodes (with degree 2) plus 1, so this optimization makes sense.
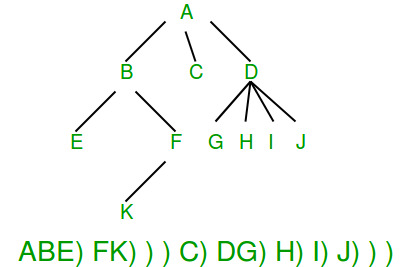
How to serialize N-ary tree?
In an N-ary tree, there is no designated left or right child. We can store an ‘end of children‘ marker with every node. The following diagram shows serialization where ‘)’ is used as the end of the children marker. We will soon be covering implementation for N-ary tree.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...