Central limit theorem in R

The Central Limit Theorem (CLT) is like a special rule in statistics. It says that if you gather a bunch of data and calculate the average, even if the original data doesn’t look like a neat bell-shaped curve, the averages of those groups will start to look like one if you have enough data.

What is the Central limit theorem?

The Central Limit theorem states that the distributions of the sample mean of the identically, independent, randomly selected distributions from any population, converge towards the normal distributions (a bell-shaped curve) as the sample size increases, even if the population distribution is not normally distributed.

Or

Let 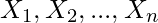be independent and identically distributed (i.i.d.) random variables drawn from the populations with the common mean 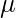and variance 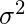. Then, as the sample size n approaches infinity i.e. 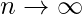, the sampling distribution of the sample mean 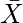will converge to a normal distribution with mean 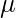and variance .

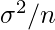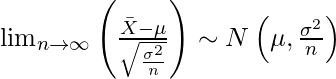
Assumptions for Central Limit Theorem

The key assumptions for the Central Limit Theorem (CLT) are as follows:

• Independence: The random variables in the sample must be independent of each other.
• Identical Distribution: The random variables are identically distributed means each observation is drawn from the same probability distribution with the same mean 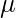and the same variance .
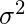• Sample Size: Sample Size (n) should be sufficiently large, typically 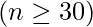, for the Central Limit Theorem CLT to provide accurate approximations.

Properties of Central limit theorem

Some of the key properties of the CLT are as follows:

• Regardless of the shape of the population distribution, the sampling distribution of the sample mean 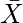approaches a normal distribution as the sample size n increases.
  
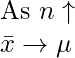
• As the sample size n increases, The sampling distribution’s variance will be equal to the variance of the population distribution divided by the sample size:
  

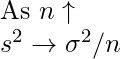
Applications of Central Limit Theorem

• The CLT is widely used in scenarios where the characteristics of the population have to be identified but analysing the complete population is difficult.
• In data science, the CLT is used to make accurate assumptions of the population in order to build a robust statistical model.
• In applied machine learning, the CLT helps to make inferences about the model performance.
• In statistical hypothesis testing the central limit theorem is used to check if the given sample belongs to a designated population.
• CLT is used in calculating the mean family income in a particular country.
• The concept of the CLT is used in election polls to estimate the percentage of people supporting a particular candidate as confidence intervals.
• The CLT is used in rolling many identical, unbiased dice.
• Flipping many coins will result in a normal distribution for the total number of heads or, equivalently, total number of tails.

Applying the Central Limit Theorem in R

To illustrate the Central Limit Theorem in R, we’ll follow these steps:

1. Generate a Non-Normally Distributed Population

Let’s start by creating a population that is not normally distributed. We’ll use a random sample from a uniform distribution as an example.

R

# Generate a non-normally distributed population
set.seed(42)
population <- runif(1000, min = 0, max = 1)

# Create a histogram of the population
hist(population, breaks = 20, probability = TRUE, main = "Histogram with Density Curve")

Output:

Population Distributioins

2. Draw Random Samples

Next, we’ll draw multiple random samples from this population. The sample size should be large enough for the CLT to hold (typically, a sample size of at least 30 is considered ).

R

# Set the sample size and number of samples
sample_size <- 20
num_samples <- 500

# Draw random samples
samples <- replicate(num_samples, sample(population, size = sample_size,replace = TRUE))

3. Check mean and Variance of Sample Mean and Populations

R

# Calculate sample means
sample_means <- colMeans(samples)

# FOr sample
x_bar <- mean(sample_means)
std <- sd(sample_means)

print('Sample Mean and Variance')
print(x_bar)
print(std**2)

# For Population
mu <- mean(population)
sigma <- sd(population)

print('Population Mean and Variance')
print(mu)
print((sigma**2)/sample_size)

Output:

[1] "Sample Mean and Variance"
[1] 0.4887697
[1] 0.003808397
[1] "Population Mean and Variance"
[1] 0.4882555
[1] 0.004246579

4. Plot the Sample distributions

Plot a histogram of the sample means to observe the distribution.

R

# Visualize the sample means
hist(sample_means, breaks = 15, prob = TRUE, main = "Distribution of Sample Means",
     xlab = "Sample Mean")

# Distribution Curve
curve(dnorm(x, mean = x_bar, sd = std), col = "Black", lwd = 2, add = TRUE)

Output:

Distribution of Sample Means

The resulting plot show that the distribution of sample means closely follows a normal distribution, even though the original population was not normally distributed. This is a direct demonstration of the Central Limit Theorem in action.

Example 2: Central limit theorem in R

R

# Set the random seed for reproducibility
set.seed(42)

# Generate a non-normally distributed population
population <- runif(5000, min = 0, max = 1)

# Create a histogram of the population
par(mfrow = c(1, 2))  # Set up a 1x2 grid for plotting

# Plot the histogram of the population
hist(population, breaks = 30, prob = TRUE, main = "Population Distribution",
     xlab = "Value", col = "lightblue")

# Step 2 and 3: Draw random samples and calculate sample means
sample_size <- 30
num_samples <- 300

# Empty vector to store sample means
sample_means <- c()

for (i in 1:num_samples) {
  # Take a random sample
  sample <- sample(population, size = sample_size, replace = TRUE)

  # Calculate the mean of the sample
  sample_means[i] <- mean(sample)
}

# For sample
x_bar <- mean(sample_means)
std <- sd(sample_means)

print('Sample Mean and Variance')
print(x_bar)
print(std**2)

# For Population
mu <- mean(population)
sigma <- sd(population)

print('Population Mean and Variance')
print(mu)
print((sigma**2)/sample_size)

# Plot the histogram of sample means
hist(sample_means, breaks = 30, prob = TRUE, main = "Distribution of Sample Means",
     xlab = "Sample Mean", col = "lightgreen")

# Overlay density curves
curve(dnorm(x, mean = x_bar, sd = std), col = "black", lwd = 2, add = TRUE)

# Add labels and legends
legend("topright", legend = c("Distribution Curve"),
       col = c("black"), lwd = 2)

# Reset the plot layout
par(mfrow = c(1, 1))

Output:

[1] "Sample Mean and Variance"
[1] 0.5010222
[1] 0.002745131
[1] "Population Mean and Variance"
[1] 0.5031668
[1] 0.002823829

Population and Sample DIstributions PLot