Central Tendency in R Programming
Last Updated :
05 Jul, 2023
Central Tendency is one of the features of descriptive statistics. Central tendency tells about how the group of data is clustered around the center value of the distribution. Central tendency performs the following measures:
- Arithmetic Mean
- Geometric Mean
- Harmonic Mean
- Median
- Mode
Arithmetic Mean
The arithmetic mean is simply called the average of the numbers which represents the central value of the data distribution. It is calculated by adding all the values and then dividing by the total number of observations. Formula: 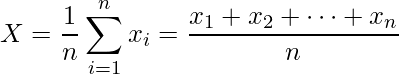 where,
where,
X indicates the arithmetic mean  indicates
indicates 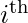 value in data vector n indicates total number of observations
value in data vector n indicates total number of observations
In R language, arithmetic mean can be calculated by the mean() function.
Syntax: mean(x, trim, na.rm = FALSE) Parameters: x: Represents object trim: Specifies number of values to be removed from each side of object before calculating the mean. The value is between 0 to 0.5 na.rm: If TRUE then removes the NA value from x
Example:
R
x <- c(3, 7, 5, 13, 20, 23, 39, 23, 40, 23, 14, 12, 56, 23)
print(mean(x))
|
Output:
[1] 21.5
Geometric Mean
The geometric mean is a type of mean that is computed by multiplying all the data values and thus, shows the central tendency for given data distribution. Formula: ![Rendered by QuickLaTeX.com \displaystyle X = \left(\prod _{i=1}^{n}x_{i}\right)^{\frac {1}{n}}={\sqrt[{n}]{x_{1}x_{2}\cdots x_{n}}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dd266cf57a0f42970aac051c751d7ec5_l3.png) where,
where,
X indicates geometric mean  indicates
indicates 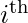 value in data vector n indicates total number of observations
value in data vector n indicates total number of observations
prod() and length() function helps in finding the geometric mean for a given set of numbers as there is no direct function for geometric mean.
Syntax:
prod(x)^(1/length(x))
where, prod() function returns the product of all values present in vector x length() function returns the length of vector x
Example:
R
x <- c(1, 5, 9, 19, 25)
print(prod(x)^(1 / length(x)))
|
Output:
[1] 7.344821
Harmonic Mean
The harmonic mean is another type of mean used as another measure of central tendency. It is computed as the reciprocal of the arithmetic mean of reciprocals of the given set of values. Formula: 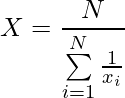 where,
where,
X indicates harmonic mean  indicates
indicates 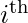 value in data vector n indicates total number of observations
value in data vector n indicates total number of observations
Example: Modifying the code to find the harmonic mean of given set of values.
R
x <- c(1, 5, 8, 10)
print(1 / mean(1 / x))
|
Output:
[1] 2.807018
Median
The median in statistics is another measure of central tendency which represents the middlemost value of a given set of values. In R language, the median can be calculated by the median() function.
Syntax: median(x, na.rm = FALSE) Parameters: x: It is the data vector na.rm: If TRUE then removes the NA value from x
Example:
R
x <- c(3, 7, 5, 13, 20, 23, 39,
23, 40, 23, 14, 12, 56, 23)
median(x)
|
Output:
[1] 21.5
Mode
The mode of a given set of values is the value that is repeated most in the set. There can exist multiple mode values in case there are two or more values with matching maximum frequency.
Since many values might occur with the highest frequency in a dataset, more than one mode value can exist in R, making the idea of mode slightly different from the mean and median.
Example 1: Single-mode value In R language, there is no function to calculate the mode. So, modifying the code to find out the mode for a given set of values.
R
x <- c(3, 7, 5, 13, 20, 23, 39,
23, 40, 23, 14, 12, 56,
23, 29, 56, 37, 45, 1, 25, 8)
y <- table(x)
print(y)
m <- names(y)[which(y == max(y))]
print(m)
|
Output:
x
1 3 5 7 8 12 13 14 20 23 25 29 37 39 40 45 56
1 1 1 1 1 1 1 1 1 4 1 1 1 1 1 1 2
[1] "23"
Example 2: Multiple Mode values
R
x <- c(3, 7, 5, 13, 20, 23, 39, 23, 40,
23, 14, 12, 56, 23, 29, 56, 37,
45, 1, 25, 8, 56, 56)
y <- table(x)
print(y)
m <- names(y)[which(y == max(y))]
print(m)
|
Output:
x
1 3 5 7 8 12 13 14 20 23 25 29 37 39 40 45 56
1 1 1 1 1 1 1 1 1 4 1 1 1 1 1 1 4
[1] "23" "56"
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...