Detecting Multicollinearity with VIF – Python
Last Updated :
10 Jan, 2023
Multicollinearity occurs when there are two or more independent variables in a multiple regression model, which have a high correlation among themselves. When some features are highly correlated, we might have difficulty in distinguishing between their individual effects on the dependent variable. Multicollinearity can be detected using various techniques, one such technique being the Variance Inflation Factor(VIF).
In VIF method, we pick each feature and regress it against all of the other features. For each regression, the factor is calculated as :
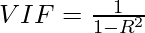
Where, R-squared is the coefficient of determination in linear regression. Its value lies between 0 and 1.
As we see from the formula, greater the value of R-squared, greater is the VIF. Hence, greater VIF denotes greater correlation. This is in agreement with the fact that a higher R-squared value denotes a stronger collinearity. Generally, a VIF above 5 indicates a high multicollinearity.
Implementing VIF using statsmodels:
statsmodels provides a function named variance_inflation_factor() for calculating VIF.
Syntax : statsmodels.stats.outliers_influence.variance_inflation_factor(exog, exog_idx)
Parameters :
- exog : an array containing features on which linear regression is performed.
- exog_idx : index of the additional feature whose influence on the other features is to be measured.
Let us see an example to implement the method on this dataset.
The dataset :
The dataset used in the example below, contains the height, weight, gender and Body Mass Index for 500 persons. Here the dependent variable is Index.
Python3
import pandas as pd
data = pd.read_csv('BMI.csv')
print(data.head())
|
Output :
Gender Height Weight Index
0 Male 174 96 4
1 Male 189 87 2
2 Female 185 110 4
3 Female 195 104 3
4 Male 149 61 3
Approach :
- Each of the feature indices are passed to variance_inflation_factor() to find the corresponding VIF.
- These values are stored in the form of a Pandas DataFrame.
Python3
from statsmodels.stats.outliers_influence import variance_inflation_factor
data['Gender'] = data['Gender'].map({'Male':0, 'Female':1})
X = data[['Gender', 'Height', 'Weight']]
vif_data = pd.DataFrame()
vif_data["feature"] = X.columns
vif_data["VIF"] = [variance_inflation_factor(X.values, i)
for i in range(len(X.columns))]
print(vif_data)
|
Output :
feature VIF
0 Gender 2.028864
1 Height 11.623103
2 Weight 10.688377
As we can see, height and weight have very high values of VIF, indicating that these two variables are highly correlated. This is expected as the height of a person does influence their weight. Hence, considering these two features together leads to a model with high multicollinearity.
Share your thoughts in the comments
Please Login to comment...