Calculus Cheat Sheet

Calculus is a branch of mathematics that studies the properties and behavior of functions, rates of change, limits, and infinite series. Calculus has many applications in science, engineering, economics, and other fields. However, calculus can also be challenging to learn and master, especially for beginners.

That is why we have prepared this calculus cheat sheet, a handy reference guide that covers the most important concepts, formulas, rules, and examples of calculus. Whether you need a quick review, a study aid, or a problem solver, this cheat sheet will help you ace calculus with ease.

What is Limit?

Limit of a function f(x) as x approaches c, denoted as lim f(x)=L, exists if for every ϵ>0, there exists a δ>0 such that for all

0 <∣x-c∣ < δ ⇒ ∣f(x)-L∣ < ϵ

Left Hand and Right Hand Limit

Left-Hand Limit	[Tex]\lim_{x \to a^{-}}f(x)=\lim_{h \to 0^{-}}f(a-h)[/Tex]
Right-Hand Limit	[Tex]\lim_{x \to a^{+}}f(x)=\lim_{h \to 0^{+}}f(a+h)[/Tex]

Existence of Limit

For Existence of [Tex]\bold{\lim_{x \to a}f(x)}  [/Tex],

• [Tex]\lim_{x \to a^{-}}f(x)  [/Tex]and [Tex]\lim_{x \to a^{+}}f(x)  [/Tex]exists, and
• [Tex]\lim_{x \to a^{-}}f(x) = \lim_{x \to a^{+}}f(x)[/Tex]

Properties of Limits

Common properties of Limits are:

[Tex]\lim _{x \rightarrow a}[f(x) \pm g(x)][/Tex]	[Tex]\lim _{x \rightarrow a} f(x) \pm \lim _{x \rightarrow a} g(x)[/Tex]
[Tex]\lim _{x \rightarrow a}[k f(x)][/Tex]	[Tex]k \lim _{x \rightarrow a} f(x),[/Tex]
[Tex]\lim _{x \rightarrow a}[f(x) g(x)][/Tex]	[Tex]\lim _{x \rightarrow a} f(x) \lim _{x \rightarrow a} g(x)[/Tex]
[Tex]\lim _{x \rightarrow a} \frac{f(x)}{g(x)}[/Tex]	[Tex]\frac{\lim _{x \rightarrow a} f(x)}{\lim _{x \rightarrow a} g(x)},  [/Tex]provided [Tex]\lim _{x \rightarrow a} g(x) \neq 0[/Tex]
[Tex]\lim _{x \rightarrow a}[f(x)]^{g(x)}[/Tex]	[Tex]\left[\lim _{x \rightarrow a} f(x)\right]^{\lim _{x \rightarrow a} g(x)}[/Tex]
[Tex]\lim _{x \rightarrow a}(g \circ f)(x)[/Tex]	[Tex]\lim _{x \rightarrow a} g[f(x)]=g\left[\lim _{x \rightarrow a} f(x)\right][/Tex]
[Tex]\lim _{x \rightarrow a} \log f(x)[/Tex]	[Tex]\log \left[\lim _{x \rightarrow a} f(x)\right],  [/Tex]provided [Tex]\lim _{x \rightarrow a} f(x)>0.[/Tex]
[Tex]\lim _{x \rightarrow a} e^{f(x)}[/Tex]	[Tex]e^{\lim _{x \rightarrow a} f(x)}[/Tex]
[Tex]\lim _{x \rightarrow a}|f(x)|[/Tex]	[Tex]\left|\lim _{x \rightarrow a} f(x)\right|[/Tex]
[Tex]\lim _{x \rightarrow a} f(x)=+\infty \ or -\infty[/Tex]	[Tex]\lim _{x \rightarrow a} \frac{1}{f(x)}=0[/Tex]

Limit Formulas

Some important formulas for limits are:

[Tex]\lim _{x \rightarrow a} \frac{x^n-a^n}{x-a}[/Tex]	[Tex]n a^{n-1}, n \in Q[/Tex]
[Tex]\lim _{x \rightarrow 0} \frac{(1+x)^n-1}{x}[/Tex]	[Tex]n, n \in Q[/Tex]
[Tex]\lim _{x \rightarrow 0} \frac{\sin x}{x}=\lim _{x \rightarrow 0} \frac{x}{\sin x}[/Tex]	1
[Tex]\lim _{x \rightarrow 0} \frac{\tan x}{x}=\lim _{x \rightarrow 0} \frac{x}{\tan x}[/Tex]	1
[Tex]\lim _{x \rightarrow 0} \frac{\sin ^{-1} x}{x}=\lim _{x \rightarrow 0} \frac{x}{\sin ^{-1} x}[/Tex]	1
[Tex]\lim _{x \rightarrow 0} \frac{\tan ^{-1} x}{x}=\lim _{x \rightarrow 0} \frac{x}{\tan ^{-1} x}[/Tex]	1
[Tex]\lim _{x \rightarrow 0} \frac{\sin x^{\circ}}{x}[/Tex]	[Tex]\frac{\pi}{180}[/Tex]
[Tex]\lim _{x \rightarrow 0} \cos x[/Tex]	1
[Tex]\lim _{x \rightarrow a} \frac{\sin (x-a)}{x-a}[/Tex]	1
[Tex]\lim _{x \rightarrow a} \frac{\tan (x-a)}{x-a}[/Tex]	1
[Tex]\lim _{x \rightarrow a} \sin ^{-1} x[/Tex]	[Tex]\sin ^{-1} a,|a| \leq 1[/Tex]
[Tex]\lim _{x \rightarrow a} \cos ^{-1} x[/Tex]	[Tex]\cos ^{-1} a,|a| \leq 1[/Tex]
[Tex]\lim _{x \rightarrow a} \tan ^{-1} x[/Tex]	[Tex]\tan ^{-1} a,-\infty<a<\infty[/Tex]
[Tex]\lim _{x \rightarrow \infty} \frac{\sin x}{x}=\lim _{x \rightarrow \infty} \frac{\cos x}{x}[/Tex]	0
[Tex]\lim _{x \rightarrow \infty} \frac{\sin \frac{1}{x}}{\frac{1}{x}}[/Tex]	1
[Tex]\lim _{x \rightarrow 0} \frac{1-\cos x}{x}[/Tex]	0
[Tex]\lim _{x \rightarrow 0} \frac{e^x-1}{x}[/Tex]	1
[Tex]\lim _{x \rightarrow 0} \frac{a^x-1}{x}[/Tex]	[Tex]\log _e a, a>0[/Tex]
[Tex]\lim _{x \rightarrow 0} \frac{\log _e(1+x)}{x}[/Tex]	1
[Tex]\lim _{x \rightarrow e} \log _e x[/Tex]	-1
[Tex]\lim _{x \rightarrow 0} \frac{\log _a(1+x)}{x}[/Tex]	[Tex]\log _a e, a>0, \neq 1[/Tex]

Learn More Limit Formulas.

Evaluation of Limits

There are various methods for evaluation of limits such as:

Substitution: This is the simplest method, where we just plug in the value of the limit into the function and see if it works. For example,

lim _{x → 2} x² + 3x − 4 = (2)² + 3(2) – 4 = 4 + 6 – 4 = 6.

Factoring: This method is helpful when substitution gives us an indeterminate form, such as 0/0 or 1⁰, where k is a constant. In this case, we can try to factor the numerator and denominator of the function and cancel out any common factors. For example, lim_{x → 2} (x² – 4)/(x − 2). If we substitute x = 2 here, limit becomes 0/0 form. Thus, it can be calculated as:

lim_{x → 2} (x² – 4)/(x − 2) = lim_{x → 2} [(x – 2)(x + 2)]/(x − 2) = lim_{x → 2} (x + 2) = 2 + 2 = 4

Algebraic manipulation: This method involves simplifying the function by using algebraic rules, such as expanding, combining, or dividing terms. For example,

lim_{x → 0} (x² + 2x)/(x² – 2x) = lim_{x → 0} x(x + 2)/x(x – 2) = lim_{x → 0} (x + 2)/(x – 2) = (0 + 2)/(0 – 2) = 2/(-2) = -1.

L Hospital Rule

If lim_{x → a} f(x)/g(x) is in the form of 0/0 or ∞/∞ then

[Tex]\lim_{x \to a}\frac{f(x)}{g(x)} = \lim_{x \to a}\frac{f'(x)}{g'(x)}[/Tex]

Where f'(x) and g'(x) are the first order derivatives of functions f(x) and g(x) respectively.

Other Indeterminant forms in limits are:

• 0 ⋅ ∞
• ∞ − ∞
• 0⁰
• 1^∞
• ∞⁰

Read More about L Hospital Rule.

Sandwich Theorem

For functions f(x), g(x), and h(x) such that f(x) ≤ g(x) ≤ h(x) then for some value ‘a’ if [Tex] \bold{\lim_{x \to a}f(x)} = p = \bold{\lim_{x \to a}h(x)} [/Tex]then

[Tex]\bold{\lim_{x \to a}g(x)= p}[/Tex]

Read more about Sandwich Theorem.

Continuity, Discontinuity, and Differentiability of a Function

The conditions for continuity, discontinuity, and differentiability of a function at a point are tabulated below:

Continuity	Discontinuity	Differentiability
[Tex]\lim_{x \to a^{-}}f(x)=\lim_{x \to a^{+}}f(x)=f(a)[/Tex]	f(a) not defined Either Left Hand Limit or Right LImit doesn’t exist or infinite [Tex]\lim_{x \to a^{-}}f(x)\neq\lim_{x \to a^{+}}f(x)[/Tex] [Tex]\lim_{x \to a^{-}}f(x)=\lim_{x \to a^{+}}f(x)\neq{f(a)}[/Tex]	[Tex]\lim_{x \to a}\frac{f(x)-f(a)}{x-a}  [/Tex]has finite value If Left Hand Derivative Right Hand Derivative i.e. [Tex]\lim_{x \to a^{-}}\frac{f(x)-f(a)}{x-a}=\lim_{x \to a^{+}}\frac{f(x)-f(a)}{x-a}[/Tex]

Theorems of Continuity

Some common theorems related to continuity are:

• If f and g are continuous functions then f±g, fg, f/g (where, g≠0), and cf(x) all are continuous.
• If g is continuous at ‘a’ and f is continuous at g(a) then fog is also continuous at ‘a’.
• If f is continuous in its domain then |f| is also continuous in its domain
• If f is continuous in the domain D then 1/f is also continuous in D-{x:f(x) = 0}.

Fundamental Theorems of Differentiability

Some common theorems related to differentiability are:

• If f and g are two differential functions then their sum, difference, product, and quotients are also differentiable.
• If f and g are two differential functions then fog is also differentiable.
• If f and g are not differential functions then their sum and product functions can be differential functions.

Learn More Continuity and Discontinuity

Derivatives

Derivative is the rate of change of a function with respect to its inputs. The derivative of a function f(x) at a particular point x, denoted as f'(x) or df/dx(x), is equal to the slope of the tangent line to the function at that point. Derivatives can be expressed as:

Derivative at a Point	[Tex]\bold{\lim_{x \to c}\frac{f(x)-f(c)}{x-c}}[/Tex]
Derivative of a Function	[Tex]\bold{f'(x) = \lim_{h \to 0} \frac{f(x + h) -f(x)}{h}}[/Tex]
Derivative as a Rate Measure	[Tex]\dfrac{dy}{dx}=\bold{\lim_{\Delta x \to 0}\dfrac{\Delta y}{\Delta x}}[/Tex]
Differentiation from the First Principle	[Tex]\bold{f'(x) = \lim_{h \to 0} \frac{f(x + h) -f(x)}{h}}[/Tex]

Algebra of Derivatives

Algebra of derivatives refers to the rules and formulas used to find the derivative of algebraic functions. Some rules for derivatives are:

Sum Rule	{f(x) + g(x)}’ = f'(x) + g'(x)
Difference Rule	{f(x) – g(x)}’ = f'(x) – g'(x)
Product Rule	{f(x).g(x)}’ = f'(x).g(x) + f(x).g'(x)
Quotient Rule	{f(x)/g(x)}’ = {f'(x).g(x) – f(x).g'(x)}/(g(x))2

Learn More, Algebra of Derivatives

Differentiation Formulas

Some of the common formulas to find derivative are:

d/dx(c)	0
d/dx{c.f(x)}	c.f'(x)
d/dx(x)	1
d/dx(xn)	nxn-1
d/dx{f(g(x))}	f'(g(x)).g'(x)
d/dx(ax)	ax.ln(a)
d/dx{ln(x)} {Note: ln(x) = loge(x)}	1/x, x>0
d/dx(logax)	1/xln(a)
d/dx(ex)	ex
d/dx{sin(x)}	cos(x)
d/dx{cos(x)}	-sin(x)
d/dx{tan(x)}	sec2x
d/dx{sec(x)}	sec(x).tan(x)
d/dx{cosec(x)}	-cosec(x).cot(x)
d/dx{cot(x)}	-cosec2(x)
d/dx{sin-1(x)}	1/√(1 – x2)
d/dx{cos-1(x)}	-1/√(1 – x2)
d/dx{tan-1(x)}	1/(1+x2)

Check,

• Differentiation of Trigonometric Functions
• Derivative of Inverse Trig Functions

Differentiation of Function of a Function

It says that if f(x) and g(x) are differentiable functions then fog is also differentiable.

d/dx{(fog)(x)} = d/dx{fog(x)}.d/dx{g(x)}

OR

y = g(x) and z = f(y), then dz/dx = (dz/dy).(dy/dx)

Differentiation Rules

Some common rules for differentiation are:

Rule	Function, f(x)	Derivative, f'(x)
Constant Multiple Rule	c ⋅f(x)	c ⋅ f′(x)
Sum Rule	f(x) + g(x)	f′(x) + g′(x)
Difference Rule	f(x) − g(x)	f′(x) − g′(x)
Product Rule	f(x)⋅g(x)	f(x)g'(x) + f'(x)g(x)
Quotient Rule	g(x)f(x)​	(g(x)f'(x) – f(x)g'(x)) / (g(x))2
Chain Rule	f(g(x))	f′(g(x))⋅g′(x)

Where f'(x) represents first order derivative of f(x).

Some of the examples of chain rule are:

d/dx[{f(x)}n]	n[{f(x)}n-1].f'(x)
d/dx[ln{f(x)}]	{1/f(x)}.f'(x)
d/dx{ef(x)}	ef(x).f'(x)
d/dx{sin(f(x))}	cos(f(x)).f'(x)
d/dx{cos(f(x))}	-sin(f(x)).f'(x)
d/dx{tan(f(x))}	sec2(f(x)).f'(x)
d/dx{tan-1(f(x))} = {1/(1+(f(x))2)}.f'(x)	{1/(1+(f(x))2)}.f'(x)

Read More,

• Chain Rule
• Product Rule
• Quotient Rule

Differentiation of Determinant

Let’s say we have to differentiate a determinant given in terms of x, then its derivative is given as differentiation of row (or column) at a time.

If [Tex]\bold{|x| = \begin{vmatrix}f(x)&g(x) \\ u(x)&v(x)\end{vmatrix}}[/Tex]

Then [Tex]\bold{|x|’ = \begin{vmatrix}f'(x)&g'(x) \\ u(x)&v(x)\end{vmatrix} + \begin{vmatrix}f(x)&g(x) \\ u'(x)&v'(x)\end{vmatrix}}[/Tex]

Where |x|’ represents the first order derivative fo |x|.

Extreme Value Theorem

If f(x) is continuous in the closed interval [a, b] then there exists c ≥ a for which f(c) is minimum and d ≤ b for which f(d) is minimum. In short, for a ≤ c and d ≤ b, f(c) is the absolute minimum in the closed interval [a, b] and f(d) is the absolute maximum in the closed interval [a, b].

Mean Value Theorem

Mean Value Theorem states that if a function f(x) is continuous in the closed interval [a, b] and differentiable in the open interval (a, b) then there exists a point c in (a, b) such that

f'(c) = [f(b) – f(a)]/(b-a)

Learn More, Rolle’s Theorem and Lagrange’s Mean Value Theorem

Implicit Differentiation

Implicit Differentiation is used when a function is not defined explicitly in terms of only one independent variable.

Let’s say we have a function g(x, y) = x² + y + 3xy

then g'(x, y) = d{g(x,y)}/dx = 2x + y’ + 3y + 3xy’ 

⇒ g'(x,y) = 2x + 3y + y'(1 + 3x).

Higher Order Derivatives

Higher Order Derivatives refer to the derivative of derivative of a function. In this, we first differentiate a function and find its derivatives and then again differentiate the derivative obtained for the first time. If differentiation is done two times then it is called Second Order Derivative and if done for ‘n’ times it is called n^th order derivative. For a function defined as y = f(x), its higher-order derivatives are given as follows:

Second Order Derivative	f”(x) = f2(x) = d2y/dx2 = {f'(x)}’
nth Order Derivative	fn(x) = dny/dxn = {f(n-1)(x)}’

Increasing and Decreasing Function

Let f(x) is a function differentiable on (a, b) then the function is

Increasing	f'(x) > 0
Decreasing	f'(x) < 0
Constant	f'(x) = 0

Learn More, Increasing and Decreasing Function

Critical Point

Critical Point is the point where the derivative of the function is either zero or not defined. C is the critical point of the function f(x) if

(dy/dx)_{x = C} = 0

OR

(dy/dx)_{x = C} = Not Defined

Concave Up and Concave Down

Concave Up	f”(x) > 0 at x = a
Concave Down	f”(x) < 0 at x = a

Inflection Point

The point at which the concavity of a function changes is called the Inflection Point. The below-mentioned steps can be used to find the inflection point:

Step 1: Find the second-order derivative of the function i.e. f”(x).

Step 2: Equate f”(x) = 0 and find x.

Step 3: Take a point smaller than x and one larger than x.

Step 4. Put the values in f”(x) and observe the sign. If the sign changes from a value lower than x to a value larger than x then an inflection point exists.

Maxima and Minima

Absolute Maximum	x = a	f(x) ≤ f(a) where x and a belong to domain of f.
Absolute Minimum	x = a	f(x) ≥ f(a) where x and a belong to  domain of f.
Local Maxima	x = a	f(x) ≤ f(a) for all x near to a.
Local Minima	x = a	f(x) ≥ f(a) for all x near to a.

Learn More, Absolute Maxima and Minima and Relative Maxima and Minima

First Derivative Test

Local Minima	Local Maxima
If x = a is point of local minima then f'(a) = 0 and f'(x) > 0 for points right to x = a and f'(x) < 0 for points left to x = a	If x = a is the point of local maxima then f'(a) = 0 and f'(x) > 0 for points left to x = a and f'(x) < 0 for points right to x = a.

Second Derivative Test

If x = a is a critical point of f(x) such that f'(a) = 0 then if

f”(a) < 0	x = a is the point of local maxima
f”(a) > 0	x = a is the point of local minima
f”(a) = 0	x = a may be a point of local maxima or local minima or none.

Differential Equation

Differential Equation refers to an equation that has a dependent variable, an independent variable, and a differential coefficient of the dependent variable with respect to the independent variable.

Order and Degree of Differential Equation

Order of Differential Equation	Degree of Differential Equation
Highest Derivative in the Equation Example: In (dy/dx)2 + 3(d2y/dx2)3 Order is 2.	Exponent raised to Highest Derivative Example: In (dy/dx)3 + 3(d2y/dx2)2 Degree is 3.

Solution of First Order and First Degree Differential Equation

The solution of a first-order and first-degree differential equation can be found by different techniques depending upon the category they belong to.

Equation of the Standard Form

If a differential equation is in the form f[f₁(x,y)]d{f₁(x,y)} + Φ[f₂(x,y)]d{f₂(x,y)} + … = 0 then each term can be integrated separately. Some of the standard terms can be replaced by the exact differentials mentioned below:

xdy + ydx	d(xy)
dx + dy	d(x + y)
(xdy – ydx)/x2	d(y/x)
(ydx – xdy)/y2	d(x/y)
(xdy + ydx)/xy	d(log xy)
(ydx – xdy)/xy	d(log x/y)
(xdy – ydx)/xy	d(log y/x)
(dx + dy)/x + y	d(log (x + y))
dx/x2 – dy/y2	d(1/y – 1/x)

Equation with Separable Variables

In the variable separable method, the equation is transformed into the form f(x)dx = g(y) and then integrated on both sides resulting in ∫f(x)dx = ∫g(y)dy + C.

Equation Reducible to Variable Separable Form	Homogeneous Differential Equation
For dy/dx = f(ax + by + c) Let ax + by + c = p ⇒ a + b(dy/dx) = dp/dx ⇒ dy/dx = 1/b(dp/dx – a). Now, dy/dx = f(ax + by + c) = f(p) ⇒ 1/b(dp/dx – a) = f(p) ⇒ dp/dx = b.f(p) + a ⇒ dp/(b.f(p) + a) = dx Thus, the equation is separated into two variables p and x,  which now can be integrated.	For dy/dx = f(x,y)/g(x,y) Let’s say dy/dx = f(y/x)/g(y/x) = F (y/x) Put y = vx ⇒ dy/dx = v + x(dv/dx) ⇒ v + x(dv/dx) = F(v) ⇒ dv/(F(v) – v) = dx/x Integrate the above equation and v must be replaced by y/x.

Read More about Homogeneous Differential Equation.

Linear Differential Equation

Form of Differential Equation	Integrating Factor (IF)	Solution
dy/dx + Ry = S	e∫Rdx	ye∫Rdx = ∫Se∫Rdx + C
dx/dy + Px = Q	e∫Pdy	ye∫Pdy = ∫Se∫Pdy + C

Integration

Integral of a function (f(x)) over an interval ([a, b]) can be expressed as:

[Tex]\int_{a}^{b} f(x) , dx[/Tex]

This notation represents the area under the curve of the function f(x) between the points x = a and x = b. To understand this concept, consider dividing the interval [a, b] into smaller subintervals. Let’s say we have n subintervals, each of width \Delta x:

[Tex]\Delta x = \frac{b – a}{n}[/Tex]

Now, we approximate the area under the curve by summing up the areas of rectangles. For each subinterval i, we take the value of f(x) at some point x_i within that subinterval and multiply it by the width (\Delta x):

(Area of rectangle)_i = [Tex]f(x_i) \cdot \Delta x[/Tex]

Riemann sum is given by:

[Tex]R_n = \sum_{i=1}^{n} f(x_i) \cdot \Delta x[/Tex]

The integral is defined as the limit of this Riemann sum as (n) approaches infinity:

[Tex]\int_{a}^{b} f(x) dx = \lim_{{n \to \infty}} R_n[/Tex]

Indefinite Integration

If the derivative of a function d/dx(Φ(x)) = f(x) then its indefinite integral is given by ∫f(x)dx = Φ(x) + C where c is the constant, f(x) is called the integrand and Φ(x) is called the integral or the antiderivative of the function f(x).

Integration Formulas

Formula for integration of various functions are:

∫xndx	xn+1/n+1 + C
∫1/xdx	loge|x| + C
∫exdx	ex + C
∫axdx	ax/logea + C
∫sin x dx	-cos x + C
∫cos x dx	sin x + C
∫sec2 x dx	tan x + C
∫cosec2 x dx	-cot x + C
∫sec x. tan x dx	sec x + C
∫cosec x cot x dx	-cosec x + C
∫tan x dx	-log |cos x| + C = log |sec x| + C
∫cot x dx	log∣sin x∣+C = −log∣cosec x∣+C
∫sec x dx	log∣sec x + tan x∣+C
∫cosec x dx	∣cosec x − cot x∣+C
∫1/√(a2 – x2)	sin-1(x/a) + C
∫-1/√(a2 – x2)	cos-1(x/a) + C
∫1/√(a2 + x2)	1/a(tan-1(x/a)) + C
∫-1/√(a2 + x2)	1/a(cot-1(x/a)) + C
∫1/x√(x2 – a2)	1/a(sec-1(x/a)) + C
∫-1/x√(x2 – a2)	1/a(cosec-1(x/a)) + C

Properties of Indefinite Integrals

Some properties of indefinite integral are:

d/dx{∫f(x)dx}	f(x)
∫k.f(x)dx	k∫f(x)dx
∫{f1(x)} ± f2(x) ± f3(x) ±…± fn(x)	∫f1(x) ± ∫f2(x) ±∫ f3(x) ±…± ∫fn(x)

Integration Techniques

There are various techniques of integration, some of which are discussed here.

Integration by Substitution

In the Integration by Substitution technique for integrating ∫f'{g(x)}g'(x)dx assume a variable t = g(x) such that g'(x) = dt/dx. Hence replace g'(x)dx by dt as g'(x)dx = dt. Thus we will get ∫f'(t)dt = f(t) + C = f{g(x)} + C

Example: [Tex]\bold{I = \int 2x e^{x^2} dx }[/Tex]

Let x² = t

⇒ 2x dx = dt

Thus, [Tex]\bold{I = \int e^{t} dt }[/Tex]

⇒ [Tex]I = e^{t} + C = e^{x^2} + C[/Tex]

Integration by Parts

Integration by Parts is used to integrate two functions given in product form given that both are integrable. The order of selection as first and second function is done by the ILATE rule which stands for Inverse, Logarithmic, Algebraic, Trigonometric, and Exponential followed in order.

The Integration is done as ∫uv.dx = u∫vdx – ∫{du.∫vdx}dx where u is the first function and v is the second function and also both u and v are functions of x.

Or we can also write, [Tex]\int f(x) \cdot g(x)dx = f(x) \int g(x) dx – \int \left( \int g(x) dx \right) f’(x) dx [/Tex]

Example: Evaluate [Tex]\bold{\int x \cdot e^x dx}[/Tex]

Let (f(x) = x) and and g(x) = e^x.

Thus, [Tex] \int x \cdot e^x dx = xe^x – \int 1 \cdot( \int ({e^x)dx) dx} = xe^x – e^x + C [/Tex]

Integration by Partial Fraction

For integrating functions given in the form of P(x)/Q(x) where P(x) and Q(x) are polynomial Functions such that the degree of P(x) is smaller than that of Q(x) then the factor of the denominator is decomposed in a partial fraction which is then integrated.

Proper Rational Fraction	Partial Function
(px + q)/(x – a)(x – b)	A/(x – a) + B/(x – b)
px2 + qx + r/(x – a)(x – b)(x – c)	A/(x – a) + B/(x – b) + C(x – c)
px + q/(x – a)3	A/(x – a) + B/(x – a)2 + C/(x – a)3
px2 + qx + r/(x – a)2(x – b)	A/(x – a) + B/(x – a)2 + C/(x – b)
px2 + qx + r/(x – a)(x2 + bx + c)	A/(x – a) + B/(x2 + bx + c)

Definite Integration

When a function f(x) is defined in the interval [a,b] then it’s antiderivative [Tex]\int_{a}^{b}f(x)dx  [/Tex]= Φ(b) – Φ(a) is called the definite integral of f(x) in the range a to b where a is the lower limit and b is the upper limit of the function.

Fundamental Theorem of Calculus

There are two Fundamental theorem of Calculus given which are mentioned below:

First Fundamental Theorem	For a function f(x) continuous in the interval [a,b] and its Area given as A(x) then A'(x) = f(x), ∀ x ∈ [a,b].
Second Fundamental Theorem	For a function f(x) continuous in the interval [a,b], and its antiderivative given by Φ then [Tex]\int_{a}^{b}f(x)dx  [/Tex]= Φ(b) – Φ(a)

Definite Integral Properties

Common properties of Definite Integral are:

[Tex]\int_{a}^b  [/Tex]f(x)dx	[Tex]-\int_{b}^a  [/Tex]f(x)dx
[Tex]\int_{a}^a  [/Tex]f(x)dx	0
[Tex]\int_{a}^b  [/Tex]f(x)dx	[Tex]\int_{a}^c  [/Tex]f(x)dx + [Tex]\int_{c}^b  [/Tex]f(x)dx, where a<c<b
[Tex]\int_{a}^b  [/Tex]f(x) ± g(x)dx	[Tex]\int_{a}^b  [/Tex]f(x)dx ± [Tex]\int_{a}^b  [/Tex]g(x)dx
[Tex]\int_{a}^{b}  [/Tex]c.f(x)dx	c.[Tex]\int_{a}^{b}  [/Tex]f(x)dx
[Tex]\int_{a}^{b}  [/Tex]f(x)dx	[Tex]\int_{a}^{b}  [/Tex]f(a + b – x) dx
[Tex]\int_{0}^{a}  [/Tex]f(x)dx	[Tex]\int_{0}^{a}  [/Tex]f(a – x) dx
[Tex]\int_{0}^{2a}  [/Tex]f(x)dx	[Tex]\int_{0}^{a}  [/Tex]f(x)dx + [Tex]\int_{0}^{a}  [/Tex]f(2a – x)dx
[Tex]\int_{-a}^{a}  [/Tex]f(x)dx	[Tex]\int_{0}^{a}  [/Tex]f(x)dx + [Tex]\int_{0}^{a}  [/Tex]f(-x)dx
[Tex]\int_{0}^{2a}  [/Tex]f(x)dx	[Tex]2\int_{0}^{a}  [/Tex]f(x)dx if f(2a – x) = f(x) 0 if f(a + x) = -f(x)
[Tex]\int_{-a}^{a}  [/Tex]f(x)dx	[Tex]2\int_{0}^{a}  [/Tex]f(x) if f(x) is even 0 if f(x) is odd
[Tex]\int_{a}^{b}  [/Tex]f(x)dx	[Tex](b-a)\int_{0}^{1}  [/Tex]f[(b – a)x + a]dx

Learn More, Properties of Definite Integrals

Application of Integration

The main application of integration is to find the area bounded by regions which is given as follows:

Area Bounded by Region	Formula	Picture
Area between curve and x-axis	A = [Tex]\int_{a}^{b}  [/Tex]f(x)dx
Area between curve and y-axis	A = [Tex]\int_{a}^{b}  [/Tex]f(y)dy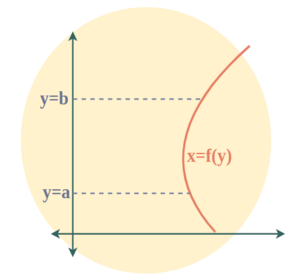
Area between Two Curves	A = [Tex]\int_{a}^{b}  [/Tex][f(x) – g(x)]dx
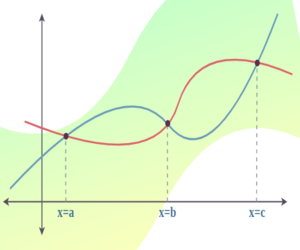
Area between Compound Curves	A = [Tex]\int_{a}^{b}  [/Tex][f(x) – g(x)]dx + [Tex]\int_{c}^{b}  [/Tex][g(x) – f(x)]dx
Area between Polar Curves	A = 1/2[Tex]\int_{\alpha}^{\beta}  [/Tex]{(r0)2 – (ri)2}dθ

Learn More, Area as Definite Integral

Volumes of Revolution

Volume of Revolution can be calculated using the formulas:

V = ∫ A(x) dx and V = ∫ A(y) dy

Where A(x) and A(y) represent the cross-sectional area functions with respect to the respective axis of rotation.

Learn More about Volumes of Revolution.

Arc Length

Arc length refers to the length of a curve between two given points. In calculus, finding the arc length of a curve involves integrating the distance formula along the curve’s path.

Given a curve represented by a function y = f(x) on an interval [a, b], the arc length formula for the curve is:

[Tex]L = \int_{a}^{b} \sqrt{1 + \left(\frac{dy}{dx}\right)^2} dx[/Tex]

Similarly, if the curve is represented parametrically by x = g(t) and y = h(t) on an interval [t₁, t|₂], the arc length formula becomes:

[Tex]L = \int_{t_1}^{t_2} \sqrt{\left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2} dt [/Tex]

Read More about Arc Length.

Improper Integral

An improper integral is an integral with one or both limits of integration being infinite or where the integrand function is unbounded within the interval of integration.

There are two types of improper integrals:

Type 1: The integrand becomes unbounded at one or both of the limits of integration. For example:

• [Tex]\int_{a}^{\infty} f(x) \, dx [/Tex]
• [Tex] \int_{-\infty}^{b} f(x) \, dx [/Tex]
• [Tex] \int_{-\infty}^{\infty} f(x) \, dx [/Tex]

To evaluate a Type 1 improper integral, you take the limit as a variable approaches infinity or negative infinity, depending on the case.

Type 2: The integrand becomes unbounded at a finite point within the interval of integration. For example:

• [Tex]\int_{a}^{b} \frac{f(x)}{(x – c)^p} ~ dx [/Tex]

Where p > 0 and a ≤ c ≤ b . Here, c is the point where the integrand becomes unbounded.

To evaluate a Type 2 improper integral, you split it into two integrals at the point of discontinuity c and then take limits for each integral.

Read More about Improper Integral.