Given an array of integers, the task is to calculate the sum of GCD of all the subarrays of an array. GCD of an array is defined as the GCD of all the elements present in it. More formally, ![GCD(A[n]) = GCD(A_1, A_2, A_3....A_n)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-58639a0aeee453c2daf2af373e94ccdf_l3.png "Rendered by QuickLaTeX.com")
. Summation of all the GCDs can be defined as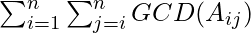 
where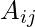 
denotes the subarray starting from ith index and ending at jth index.
Examples:
Input 1: N = 5, A = {1,2,3,4,5}
Output 1: 25
Explanation:
The subarrays of length one are [1], [2], [3], [4], [5] and the sum of their GCDs is 15, similarly subarrays of length 2, are [1, 2], [2, 3], [3, 4], [4, 5], and the sum of their GCDs is 4, similarly for length 3, the sum is 3, similarly for length 4, the sum is 2, similarly for length 5, the sum is 1.
The total sum becomes 25.
Input 2: N = 6, A = {2,2,2,3,5,5}
Output 2: 41
Pre-Requisites
Binary Search
Segment Tree approach for calculating GCD in an index range
Sparse Table for calculating GCD in an index range
Naive Approach (O(n^3) complexity)
We can find out every subarray in O(n^2) complexity and can traverse it for finding the GCD of that subarray and add it to the total answer.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int findGCDSum(int n, int a[])
{
int GCDSum = 0;
int tempGCD = 0;
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
tempGCD = 0;
for (int k = i; k <= j; k++) {
tempGCD = __gcd(tempGCD, a[k]);
}
GCDSum += tempGCD;
}
}
return GCDSum;
}
int main()
{
int n = 5;
int a[] = { 1, 2, 3, 4, 5 };
int totalSum = findGCDSum(n, a);
cout << totalSum << "\n";
}
|
Java
class GFG
{
static int findGCDSum(int n, int a[])
{
int GCDSum = 0;
int tempGCD = 0;
for (int i = 0; i < n; i++)
{
for (int j = i; j < n; j++)
{
tempGCD = 0;
for (int k = i; k <= j; k++)
{
tempGCD = __gcd(tempGCD, a[k]);
}
GCDSum += tempGCD;
}
}
return GCDSum;
}
static int __gcd(int a, int b)
{
return b == 0 ? a : __gcd(b, a % b);
}
public static void main(String[] args)
{
int n = 5;
int a[] = { 1, 2, 3, 4, 5 };
int totalSum = findGCDSum(n, a);
System.out.print(totalSum + "\n");
}
}
|
Python3
def findGCDSum(n, a):
GCDSum = 0;
tempGCD = 0;
for i in range(n):
for j in range(i, n):
tempGCD = 0;
for k in range(i, j + 1):
tempGCD = __gcd(tempGCD, a[k]);
GCDSum += tempGCD;
return GCDSum;
def __gcd(a, b):
return a if(b == 0 ) else __gcd(b, a % b);
if __name__ == '__main__':
n = 5;
a = [1, 2, 3, 4, 5];
totalSum = findGCDSum(n, a);
print(totalSum);
|
C#
using System;
class GFG
{
static int findGCDSum(int n, int []a)
{
int GCDSum = 0;
int tempGCD = 0;
for (int i = 0; i < n; i++)
{
for (int j = i; j < n; j++)
{
tempGCD = 0;
for (int k = i; k <= j; k++)
{
tempGCD = __gcd(tempGCD, a[k]);
}
GCDSum += tempGCD;
}
}
return GCDSum;
}
static int __gcd(int a, int b)
{
return b == 0 ? a : __gcd(b, a % b);
}
public static void Main(String[] args)
{
int n = 5;
int []a = { 1, 2, 3, 4, 5 };
int totalSum = findGCDSum(n, a);
Console.Write(totalSum + "\n");
}
}
|
Javascript
<script>
function findGCDSum(n , a)
{
var GCDSum = 0;
var tempGCD = 0;
for (i = 0; i < n; i++)
{
for (j = i; j < n; j++)
{
tempGCD = 0;
for (k = i; k <= j; k++)
{
tempGCD = __gcd(tempGCD, a[k]);
}
GCDSum += tempGCD;
}
}
return GCDSum;
}
function __gcd(a , b)
{
return b == 0 ? a : __gcd(b, a % b);
}
var n = 5;
var a = [ 1, 2, 3, 4, 5 ];
var totalSum = findGCDSum(n, a);
document.write(totalSum + "<br/>");
</script>
|
Time Complexity: O(N^3)
Space Complexity: O(1)
We can optimize the part where you calculate GCD of a subarray, We can use a segment tree or a sparse table to optimize the complexity to O(n^2 * logn) (for segment trees) or to O(n^2) (for sparse table)
Efficient Approach (O(n*(logn)^2) complexity):
This approach takes advantage of the observation that upon adding a new element to an array, the new GCD of the array will always be either less or equal to the previous GCD of the array before the addition of the element.
We create three pointers, lets call them startPointer, endPointer and prevEndPointer. Initially all three of them point to the first element of our array. We initialize a variable tempGCD with the value of the first element. We will now find the sum of GCDs of all the subarrays starting with first element.
Now according to our previous observation, if we move the endPointer to the right by one position, and calculate the GCD of these two elements which are pointed by startPointer and endPointer, it will always be less than or equal to tempGCD. So if we want to find out how many subarrays have the GCD as tempGCD, we need to find a suitable position of endPointer, where the subarray starting at startPointer and ending at endPointer will have the value of it’s GCD less than tempGCD, and the value of endPointer should be as minimal as possible, then the difference of prevEndPointer and endPointer will give us the number of subarrays which have their GCD as tempGCD. Now, we can add this value (tempGCD*(endPointer-prevEndPointer)), which denotes the sum of the GCD for these particular group of subarrays, into our variable finalAns which stores the sum of the GCD of all subarrays.
Now the question remains, how will we find the suitable position of endPointer where the GCD decreases? That’s where Binary Search comes into use, we have the starting point of our array fixed, and we need to vary the ending point, let’s call them L and R, so for any R. We initialize high as N and low as prevEndPointer, and mid as (high+low)/2, now if we check the value of GCD[L, mid], we compare it to the value of tempGCD, and if it is less than it, then R might be a suitable position for endPointer, but it might be the case that some smaller value may become our answer, so we change high to be mid-1, and if GCD[L, mid] is found to be equal to tempGCD, then we should change low to be mid+1, and the value of mid+1 might be the answer, so we store the value of mid in a variable nextPos. At last we return the value of nextPos+1.
Value of GCD[L, mid] can be efficiently calculated using a Segment Tree in O(logN) complexity or using a Sparse Table in O(1) complexity.
This type of binary search finds us the suitable position of endPointer. After finding out this position, and adding to finalAns, we change prevEndPointer to endPointer, and tempGCD to GCD[startPointer, endPointer], and again start the process of finding next endPointer. This will stop once the value of endPointer becomes N, and then we need to move startPointer to the right, which will count the sum of GCD of all subarrays starting with second element. This will continue till the value of startPointer becomes N.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int SparseTable[100001][51];
void buildSparseTable(int a[], int n)
{
for (int i = 0; i < n; i++) {
SparseTable[i][0] = a[i];
}
for (int j = 1; j <= 19; j++) {
for (int i = 0; i <= n - (1 << j); i++) {
SparseTable[i][j] = __gcd(SparseTable[i][j - 1],
SparseTable[i + (1 << (j - 1))][j - 1]);
}
}
}
int queryForGCD(int L, int R)
{
int returnValue;
int j = int(log2(R - L + 1));
returnValue = __gcd(SparseTable[L][j],
SparseTable[R - (1 << j) + 1][j]);
return returnValue;
}
int nextPosition(int tempGCD, int startPointer,
int prevEndPointer, int n)
{
int high = n - 1;
int low = prevEndPointer;
int mid = prevEndPointer;
int nextPos = prevEndPointer;
while (high >= low) {
mid = ((high + low) >> 1);
if (queryForGCD(startPointer, mid) == tempGCD) {
nextPos = mid;
low = mid + 1;
}
else {
high = mid - 1;
}
}
return nextPos + 1;
}
int calculateSum(int a[], int n)
{
buildSparseTable(a, n);
int endPointer, startPointer, prevEndPointer, tempGCD;
int tempAns = 0;
for (int i = 0; i < n; i++) {
endPointer = i;
startPointer = i;
prevEndPointer = i;
tempGCD = a[i];
while (endPointer < n) {
endPointer = nextPosition(tempGCD, startPointer,
prevEndPointer, n);
tempAns += ((endPointer - prevEndPointer) * tempGCD);
prevEndPointer = endPointer;
if (endPointer < n) {
tempGCD = __gcd(tempGCD, a[endPointer]);
}
}
}
return tempAns;
}
int main()
{
int n = 6;
int a[] = {2, 2, 2, 3, 5, 5};
cout << calculateSum(a, n) << "\n";
return 0;
}
|
Java
class GFG
{
static int [][]SparseTable = new int[100001][51];
static void buildSparseTable(int a[], int n)
{
for (int i = 0; i < n; i++)
{
SparseTable[i][0] = a[i];
}
for (int j = 1; j <= 19; j++)
{
for (int i = 0; i <= n - (1 << j); i++)
{
SparseTable[i][j] = __gcd(SparseTable[i][j - 1],
SparseTable[i + (1 << (j - 1))][j - 1]);
}
}
}
static int queryForGCD(int L, int R)
{
int returnValue;
int j = (int) (Math.log(R - L + 1));
returnValue = __gcd(SparseTable[L][j],
SparseTable[R - (1 << j) + 1][j]);
return returnValue;
}
static int nextPosition(int tempGCD, int startPointer,
int prevEndPointer, int n)
{
int high = n - 1;
int low = prevEndPointer;
int mid = prevEndPointer;
int nextPos = prevEndPointer;
while (high >= low)
{
mid = ((high + low) >> 1);
if (queryForGCD(startPointer, mid) == tempGCD)
{
nextPos = mid;
low = mid + 1;
}
else
{
high = mid - 1;
}
}
return nextPos + 1;
}
static int calculateSum(int a[], int n)
{
buildSparseTable(a, n);
int endPointer, startPointer,
prevEndPointer, tempGCD;
int tempAns = 0;
for (int i = 0; i < n; i++)
{
endPointer = i;
startPointer = i;
prevEndPointer = i;
tempGCD = a[i];
while (endPointer < n)
{
endPointer = nextPosition(tempGCD, startPointer,
prevEndPointer, n);
tempAns += ((endPointer -
prevEndPointer) * tempGCD);
prevEndPointer = endPointer;
if (endPointer < n)
{
tempGCD = __gcd(tempGCD, a[endPointer]);
}
}
}
return tempAns;
}
static int __gcd(int a, int b)
{
return b == 0? a:__gcd(b, a % b);
}
public static void main(String[] args)
{
int n = 6;
int a[] = {2, 2, 2, 3, 5, 5};
System.out.println(calculateSum(a, n));
}
}
|
Python3
from math import gcd as __gcd,log,floor
SparseTable = [ [0 for i in range(51)] for i in range(100001)]
def buildSparseTable(a, n):
for i in range(n):
SparseTable[i][0] = a[i]
for j in range(1,20):
for i in range(n - (1 << j)+1):
SparseTable[i][j] = __gcd(SparseTable[i][j - 1],
SparseTable[i + (1 << (j - 1))][j - 1])
def queryForGCD(L, R):
j = floor(log(R - L + 1, 2))
returnValue = __gcd(SparseTable[L][j],
SparseTable[R - (1 << j) + 1][j])
return returnValue
def nextPosition(tempGCD, startPointer,prevEndPointer, n):
high = n - 1
low = prevEndPointer
mid = prevEndPointer
nextPos = prevEndPointer
while (high >= low):
mid = ((high + low) >> 1)
if (queryForGCD(startPointer, mid) == tempGCD):
nextPos = mid
low = mid + 1
else:
high = mid - 1
return nextPos + 1
def calculateSum(a, n):
buildSparseTable(a, n)
tempAns = 0
for i in range(n):
endPointer = i
startPointer = i
prevEndPointer = i
tempGCD = a[i]
while (endPointer < n):
endPointer = nextPosition(tempGCD,
startPointer,prevEndPointer, n)
tempAns += ((endPointer - prevEndPointer) * tempGCD)
prevEndPointer = endPointer
if (endPointer < n):
tempGCD = __gcd(tempGCD, a[endPointer])
return tempAns
if __name__ == '__main__':
n = 6
a = [2, 2, 2, 3, 5, 5]
print(calculateSum(a, n))
|
C#
using System;
class GFG
{
static int [,]SparseTable = new int[100001,51];
static void buildSparseTable(int []a, int n)
{
for (int i = 0; i < n; i++)
{
SparseTable[i,0] = a[i];
}
for (int j = 1; j <= 19; j++)
{
for (int i = 0; i <= n - (1 << j); i++)
{
SparseTable[i,j] = __gcd(SparseTable[i,j - 1],
SparseTable[i + (1 << (j - 1)),j - 1]);
}
}
}
static int queryForGCD(int L, int R)
{
int returnValue;
int j = (int) (Math.Log(R - L + 1));
returnValue = __gcd(SparseTable[L,j],
SparseTable[R - (1 << j) + 1,j]);
return returnValue;
}
static int nextPosition(int tempGCD, int startPointer,
int prevEndPointer, int n)
{
int high = n - 1;
int low = prevEndPointer;
int mid = prevEndPointer;
int nextPos = prevEndPointer;
while (high >= low)
{
mid = ((high + low) >> 1);
if (queryForGCD(startPointer, mid) == tempGCD)
{
nextPos = mid;
low = mid + 1;
}
else
{
high = mid - 1;
}
}
return nextPos + 1;
}
static int calculateSum(int []a, int n)
{
buildSparseTable(a, n);
int endPointer, startPointer,
prevEndPointer, tempGCD;
int tempAns = 0;
for (int i = 0; i < n; i++)
{
endPointer = i;
startPointer = i;
prevEndPointer = i;
tempGCD = a[i];
while (endPointer < n)
{
endPointer = nextPosition(tempGCD, startPointer,
prevEndPointer, n);
tempAns += ((endPointer -
prevEndPointer) * tempGCD);
prevEndPointer = endPointer;
if (endPointer < n)
{
tempGCD = __gcd(tempGCD, a[endPointer]);
}
}
}
return tempAns;
}
static int __gcd(int a, int b)
{
return b == 0? a:__gcd(b, a % b);
}
public static void Main(String[] args)
{
int n = 6;
int []a = {2, 2, 2, 3, 5, 5};
Console.WriteLine(calculateSum(a, n));
}
}
|
Javascript
<script>
let SparseTable = new Array(100001);
for(let i=0;i<100001;i++)
{
SparseTable[i]=new Array(51);
for(let j=0;j<51;j++)
{
SparseTable[i][j]=0;
}
}
function buildSparseTable(a,n)
{
for (let i = 0; i < n; i++)
{
SparseTable[i][0] = a[i];
}
for (let j = 1; j <= 19; j++)
{
for (let i = 0; i <= n - (1 << j); i++)
{
SparseTable[i][j] = __gcd(SparseTable[i][j - 1],
SparseTable[i + (1 << (j - 1))][j - 1]);
}
}
}
function queryForGCD(L,R)
{
let returnValue;
let j = Math.floor(Math.log(R - L + 1));
returnValue = __gcd(SparseTable[L][j],
SparseTable[R - (1 << j) + 1][j]);
return returnValue;
}
function nextPosition(tempGCD,startPointer,prevEndPointer,n)
{
let high = n - 1;
let low = prevEndPointer;
let mid = prevEndPointer;
let nextPos = prevEndPointer;
while (high >= low)
{
mid = ((high + low) >> 1);
if (queryForGCD(startPointer, mid) == tempGCD)
{
nextPos = mid;
low = mid + 1;
}
else
{
high = mid - 1;
}
}
return nextPos + 1;
}
function calculateSum(a,n)
{
buildSparseTable(a, n);
let endPointer, startPointer,
prevEndPointer, tempGCD;
let tempAns = 0;
for (let i = 0; i < n; i++)
{
endPointer = i;
startPointer = i;
prevEndPointer = i;
tempGCD = a[i];
while (endPointer < n)
{
endPointer = nextPosition(tempGCD, startPointer,
prevEndPointer, n);
tempAns += ((endPointer -
prevEndPointer) * tempGCD);
prevEndPointer = endPointer;
if (endPointer < n)
{
tempGCD = __gcd(tempGCD, a[endPointer]);
}
}
}
return tempAns;
}
function __gcd(a,b)
{
return b == 0? a: __gcd(b, a % b);
}
let n = 6;
let a=[2, 2, 2, 3, 5, 5];
document.write(calculateSum(a, n));
</script>
|
Time Complexity: O(N * log(max(A[i]) * log(N))
The time complexity of the above solution includes the knowledge of knowing how many times the binary search will be called, and hence we need to know how many times value of endPointer may change. This value comes out to be approximately log(A[i]), because, for any number X, the number of times it’s GCD can decrease upon being clubbed with other number is the value of highest power of any of it’s prime divisors. So the total time complexity becomes approximately O(N * log(max(A[i]) * log(N)) where another logN factor comes due to Binary search. This is the case when we use Sparse Table, if we use Segment Tree for GCD queries, another term of log(N) will appear.
Related Topic: Segment Tree