Write a program to Calculate Size of a tree | Recursion

Difficulty Level : Easy
Last Updated : 02 Jul, 2021

Size of a tree is the number of elements present in the tree. Size of the below tree is 5.

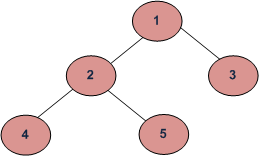
Example Tree

Size() function recursively calculates the size of a tree. It works as follows:
Size of a tree = Size of left subtree + 1 + Size of right subtree.

Algorithm:

size(tree)
1. If tree is empty then return 0
2. Else
     (a) Get the size of left subtree recursively  i.e., call 
          size( tree->left-subtree)
     (a) Get the size of right subtree recursively  i.e., call 
          size( tree->right-subtree)
     (c) Calculate size of the tree as following:
            tree_size  =  size(left-subtree) + size(right-
                               subtree) + 1
     (d) Return tree_size

C++

// A recursive C++ program to
// calculate the size of the tree
#include <bits/stdc++.h>
using namespace std;
 
/* A binary tree node has data, pointer to left child
and a pointer to right child */
class node
{
    public:
    int data;
    node* left;
    node* right;
};
 
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
node* newNode(int data)
{
    node* Node = new node();
    Node->data = data;
    Node->left = NULL;
    Node->right = NULL;
         
    return(Node);
}
 
/* Computes the number of nodes in a tree. */
int size(node* node)
{
    if (node == NULL)
        return 0;
    else
        return(size(node->left) + 1 + size(node->right));
}
 
/* Driver code*/
int main()
{
    node *root = newNode(1);
    root->left = newNode(2);
    root->right = newNode(3);
    root->left->left = newNode(4);
    root->left->right = newNode(5);
     
    cout << "Size of the tree is " << size(root);
    return 0;
}
 
// This code is contributed by rathbhupendra

C

#include <stdio.h>
#include <stdlib.h>
 
/* A binary tree node has data, pointer to left child
   and a pointer to right child */
struct node
{
    int data;
    struct node* left;
    struct node* right;
};
 
/* Helper function that allocates a new node with the
   given data and NULL left and right pointers. */
struct node* newNode(int data)
{
  struct node* node = (struct node*)
                       malloc(sizeof(struct node));
  node->data = data;
  node->left = NULL;
  node->right = NULL;
   
  return(node);
}
 
/* Computes the number of nodes in a tree. */
int size(struct node* node)
{ 
  if (node==NULL)
    return 0;
  else    
    return(size(node->left) + 1 + size(node->right)); 
}
 
/* Driver program to test size function*/   
int main()
{
  struct node *root = newNode(1);
  root->left        = newNode(2);
  root->right       = newNode(3);
  root->left->left  = newNode(4);
  root->left->right = newNode(5);  
 
  printf("Size of the tree is %d", size(root)); 
  getchar();
  return 0;
}

Java

// A recursive Java program to calculate the size of the tree
 
/* Class containing left and right child of current
   node and key value*/
class Node
{
    int data;
    Node left, right;
 
    public Node(int item)
    {
        data = item;
        left = right = null;
    }
}
 
/* Class to find size of Binary Tree */
class BinaryTree
{
    Node root;
 
    /* Given a binary tree. Print its nodes in level order
       using array for implementing queue */
    int size()
    {
        return size(root);
    }
 
    /* computes number of nodes in tree */
    int size(Node node)
    {
        if (node == null)
            return 0;
        else
            return(size(node.left) + 1 + size(node.right));
    }
 
    public static void main(String args[])
    {
        /* creating a binary tree and entering the nodes */
        BinaryTree tree = new BinaryTree();
        tree.root = new Node(1);
        tree.root.left = new Node(2);
        tree.root.right = new Node(3);
        tree.root.left.left = new Node(4);
        tree.root.left.right = new Node(5);
 
        System.out.println("The size of binary tree is : "
                            + tree.size());
    }
}

Python

# Python Program to find the size of binary tree
 
# A binary tree node
class Node:
 
    # Constructor to create a new node
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None
 
# Computes the number of nodes in tree
def size(node):
    if node is None:
        return 0
    else:
        return (size(node.left)+ 1 + size(node.right))
 
 
# Driver program to test above function
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left  = Node(4)
root.left.right = Node(5)
 
print "Size of the tree is %d" %(size(root))
 
# This code is contributed by Nikhil Kumar Singh(nickzuck_007)

C#

using System;
 
// A recursive C# program to calculate the size of the tree
 
/* Class containing left and right child of current
   node and key value*/
public class Node
{
    public int data;
    public Node left, right;
 
    public Node(int item)
    {
        data = item;
        left = right = null;
    }
}
 
/* Class to find size of Binary Tree */
public class BinaryTree
{
    public Node root;
 
    /* Given a binary tree. Print its nodes in level order
       using array for implementing queue */
    public virtual int size()
    {
        return size(root);
    }
 
    /* computes number of nodes in tree */
    public virtual int size(Node node)
    {
        if (node == null)
        {
            return 0;
        }
        else
        {
            return (size(node.left) + 1 + size(node.right));
        }
    }
 
    public static void Main(string[] args)
    {
        /* creating a binary tree and entering the nodes */
        BinaryTree tree = new BinaryTree();
        tree.root = new Node(1);
        tree.root.left = new Node(2);
        tree.root.right = new Node(3);
        tree.root.left.left = new Node(4);
        tree.root.left.right = new Node(5);
 
        Console.WriteLine("The size of binary tree is : " + tree.size());
    }
}
 
  //  This code is contributed by Shrikant13

Javascript

<script>
 
      // A recursive JavaScript program to
      // calculate the size of the tree
 
      /* Class containing left and right child of current
         node and key value*/
      class Node {
        constructor(item) {
          this.data = item;
          this.left = null;
          this.right = null;
        }
      }
 
      /* Class to find size of Binary Tree */
      class BinaryTree {
        constructor() {
          this.root = null;
        }
        /* computes number of nodes in tree */
        size(node = this.root) {
          if (node == null) {
            return 0;
          } else {
            return this.size(node.left) + 1 + this.size(node.right);
          }
        }
      }
      /* creating a binary tree and entering the nodes */
      var tree = new BinaryTree();
      tree.root = new Node(1);
      tree.root.left = new Node(2);
      tree.root.right = new Node(3);
      tree.root.left.left = new Node(4);
      tree.root.left.right = new Node(5);
 
      document.write("Size of the tree is " + tree.size() + "<br>");
       
</script>

Output:

Size of the tree is 5

Time & Space Complexities: Since this program is similar to traversal of tree, time and space complexities will be same as Tree traversal (Please see our Tree Traversal post for details)

Attention reader! Don’t stop learning now. Get hold of all the important DSA concepts with the DSA Self Paced Course at a student-friendly price and become industry ready. To complete your preparation from learning a language to DS Algo and many more, please refer Complete Interview Preparation Course.

In case you wish to attend live classes with experts, please refer DSA Live Classes for Working Professionals and Competitive Programming Live for Students.

My Personal Notes