Program to Calculate e^x by Recursion ( using Taylor Series )
Last Updated :
16 Sep, 2021
The value of the Exponential function can be calculated using Taylor Series.
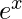 = 1 + x/1! +
= 1 + x/1! + 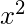 /2! +
/2! + 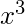 /3! + ...... + until n terms
/3! + ...... + until n terms
As the number of terms increases the more precise value of ex is obtained.
To find e^x using the recursive function, we need to use static variables. A function can return only one value, and when we need to include multiple values in a recursive function, we use static variables. The Taylor Series is a combination of multiple values like sum, power and factorial term, hence we will use static variables.
For the power of x, we will use p, and for factorials, we will use f as static variables.
The function shown below is used to increase the power of x.
p = p*x
The function below is used to find factorials.
f = f*n
The function below is used to calculate the summation of the series.
r+p/f
Where r is the recursive call to the function.
Below is the implementation of the above idea.
C++
#include <iostream>
using namespace std;
double e(int x, int n)
{
static double p = 1, f = 1;
double r;
if (n == 0)
return 1;
r = e(x, n - 1);
p = p * x;
f = f * n;
return (r + p / f);
}
int main()
{
int x = 4, n = 15;
cout<<"\n"<< e(x, n);
return 0;
}
|
C
#include <stdio.h>
double e(int x, int n)
{
static double p = 1, f = 1;
double r;
if (n == 0)
return 1;
r = e(x, n - 1);
p = p * x;
f = f * n;
return (r + p / f);
}
int main()
{
int x = 4, n = 15;
printf("%lf \n", e(x, n));
return 0;
}
|
Java
import java.text.*;
class GFG {
static double p = 1, f = 1;
static double e(int x, int n)
{
double r;
if (n == 0)
return 1;
r = e(x, n - 1);
p = p * x;
f = f * n;
return (r + p / f);
}
public static void main(String[] args)
{
int x = 4, n = 15;
DecimalFormat df = new DecimalFormat("0.######");
System.out.println(df.format(e(x, n)));
}
}
|
Python3
p = 1.0
f = 1.0
def e(x, n):
global p, f
if (n == 0):
return 1
r = e(x, n - 1)
p = p * x
f = f * n
return (r + p / f)
x = 4
n = 15
print(e(x, n))
|
C#
using System;
class GFG {
static double p = 1, f = 1;
static double e(int x, int n)
{
double r;
if (n == 0)
return 1;
r = e(x, n - 1);
p = p * x;
f = f * n;
return (r + p / f);
}
static void Main()
{
int x = 4, n = 15;
Console.WriteLine(Math.Round(e(x, n), 6));
}
}
|
Javascript
<script>
p = 1, f = 1;
function e(x, n)
{
var r;
if (n == 0)
return 1;
r = e(x, n - 1);
p = p * x;
f = f * n;
return (r + p / f);
}
var x = 4, n = 15;
var res = e(x, n);
document.write(res.toFixed(6));
</script>
|
Time Complexity:
To find this we will determine the total multiplication performed.
e^x = 1 + x/1! + x^2/2! + x^3/3! + …… + until n terms
= 1 + x/1 + x*x/1*2 + x*x*x/1*2*3 + x*x*x*x/1*2*3*4 …… + until n terms
0 0 2 4 8 Number of Multiplications in above terms
So, for n terms total multiplication performed is comparable to sum of n natural numbers (as a parallel series of even numbers is formed).
and we know sum of n natural numbers = n*(n+1)/2 whose order is n2
Hence, the time complexity if this approach is O(n2)
Auxiliary Space:
The recursive call will take place n+1 times and hence n + 1 activation records will get created at max. That shows the space complexity is O(n).
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...